慣性衛星緊組合導航系統自主完好性算法研究

管春洋，劉 洋，何 偉，郭玉勝

(北京自動化控制設備研究所，北京 100074)

0 引言

組合導航系統利用慣導、衛星導航接收機、氣壓高度表等多個硬件設備的信息，通過卡爾曼濾波器進行數據融合，實現長航時、高精度、高可靠性的導航[1]。

組合導航系統主要利用慣性導航系統和衛星導航系統進行數據融合，其中衛星導航接收機利用衛星信號進行導航信息解算，容易受到環境或人為因素的干擾，導致組合導航系統輸出導航信息異常。國內外學者對組合導航系統的自主完好性檢測算法及衛星導航接收機的故障檢測算法進行了研究，設計了快照法，如最小二乘檢測、奇偶矢量檢測等方法，可以很好地檢驗突變故障[2-4]；設計了自主完好性外推法，實現了對緩變故障的檢測；對于組合導航系統而言，設計了基于卡爾曼數據融合濾波器的卡方檢驗法[5-6]。上述方法均是從接收機或者數據融合濾波器的角度進行故障檢測[7-8]，快照法存在無法檢測緩變故障的缺點，自主完好性外推方法存在故障檢出延遲和運算量大等缺點[9]，卡爾曼濾波卡方檢驗法存在不能檢出緩變故障等缺點[10]。

本文提出了一種組合導航系統自主完好性檢測算法，在組合導航系統級利用氣壓高度輔助最小二乘檢測算法，對衛星導航接收機突變和緩變故障進行檢測。利用組合導航系統卡方檢驗方法進行故障識別，若為突變故障，對故障進行隔離；若為緩變故障，組合導航系統切換為純慣性導航模式。該方案利用慣性導航、氣壓高度等冗余信息實現了對突變和緩變故障的檢測和隔離，無需增加傳感器，實現了組合導航系統在復雜環境下的高精度、長航時的導航定位。

1 組合導航系統故障分類

1.1 外部環境異常

衛星導航接收機利用導航衛星下發的電磁波信息進行定位和測速，衛星導航接收機和導航衛星都可能存在故障。常見的故障主要有衛星上的電子故障、衛星播發的星歷與時鐘模型錯誤、異常大氣層延時、多路徑及接收機故障等。在慣性/衛星緊組合系統中，衛星故障帶來的后果表現為測量偽距值包含有故障等效偏差，并且由于量測量偽距差的變化，影響了導航的最終結果。

1.2 欺騙式干擾

欺騙式干擾信號可以正常地被衛星導航接收機捕獲與跟蹤，并參與到衛星導航接收機的定位解算中。通過更改星歷或者調整信號發射時間來達到干擾定位結果的目的。欺騙式干擾通常又分為生成式干擾與轉發式干擾，生成式干擾通過生成特定的衛星導航信號來達到干擾定位結果的目的。而轉發式干擾則通過轉發真實的衛星信號干擾偽距跟蹤結果來達到干擾定位結果的目的[11]。

2 組合導航系統故障檢測算法

組合導航系統采用最小二乘殘差法[12]對衛星的偽距進行故障檢測，本文提出的氣壓高度輔助最小二乘殘差法實現了4顆星定位時的故障檢測，輸出定位結果的同時完成故障檢測；同時組合導航系統的故障檢測采用卡爾曼濾波殘差法檢驗[13]，實現了對突變故障的識別。

2.1 氣壓高度輔助的最小二乘檢測算法

利用氣壓高度傳感器修正后的氣壓高度進行衛星導航接收機的故障檢測是可以滿足精度需求的。氣壓高度輔助下的衛星導航接收機的故障檢測算法是利用最小二乘殘差法對接收機的自主完好性進行檢測，對觀測方程進行更改。

假設衛星導航接收機觀測的觀測方程如式(1)所示，則狀態變量x的最小二乘解如式(2)所示。

y=Gx+ε

(1)

x=(GTG)-1GTy0

(2)

其中，G矩陣即為導航星座的雅克比矩陣，矩陣的最后一行為氣壓高度虛擬衛星的位置矢量，具體形式如式(3)所示。

(3)

結合式(3)推導得到偽距殘差向量Δy如式(4)所示，其中S=I-G(GTG)-1GT為偽距殘差協因數矩陣。

Δy=y0-y

=(I-G(GTG)-1GT)ε

=Sε

(4)

由于矩陣G(GTG)-1GT的秩為4，進而可以推導得到

(5)

其中，n為可觀測衛星的數目，由式(4) 、式(5) 可得偽距殘差Δy的平方和θ=ΔyT×Δy,如式(6)所示。

(6)

由以上推導再結合卡方分布的定義可知，若不存在故障衛星，即偽距誤差服從正態分布，且滿足E(ε)=0時，則偽距最小二乘殘差的平方和θ的歸一化變量θ/σ2滿足以0為中心的自由度為n-4的χ2分布，其中σ2為偽距誤差的方差。

當衛星存在故障時，設故障所引起的偽距誤差矢量為b,如式(7)所示，其中，N為故障衛星的數量，偽距殘差Δy改寫為式(8)所示。

(7)

Δy=S(ε0+b)

(8)

此時偽距誤差無法滿足E(ε)=0，則結合χ2分布的定義，并結合之前的推導可知，此時偽距殘差Δy的平方和θ的歸一化變量θ/σ2，滿足以λ為中心的自由度為n-4的χ2分布。

經過上面的計算完成了基于最小二乘殘差法的氣壓輔助衛星導航接收機的故障檢測，經過分析可知，氣壓輔助下的故障檢測可以提高衛星導航接收機故障檢測的冗余度。在衛星導航接收機收到4顆星時即可進行故障檢測，當收到5顆及以上的衛星時就可以完成故障的排除，提高了衛星導航接收機故障檢測的實用程度。在衛星導航接收機可以定位時就可以進行故障檢測，提高了衛星導航接收機導航信息的可靠性。

2.2 組合導航系統卡爾曼濾波殘差卡方檢驗

文獻[1]中提出了一種基于組合導航系統卡爾曼濾波殘差卡方檢驗法的故障檢測數據融合算法，該算法利用新息構造故障檢測函數實現對故障的檢測。

將組合導航系統做分段線性化處理，得到如下的線性系統表達式：

xk=Φk/k-1xk-1+wk-1

yk=Hkxk+vk

(9)

式中：xk為n維狀態向量；Φk/k-1為狀態轉移矩陣；yk為m維量測向量；Hk為量測矩陣；wk-1、vk為相互獨立的白噪聲向量。組合導航系統的卡爾曼濾波殘差為：

rk=yk-yk/k-1=yk-Hkxk/k-1

(10)

式中：xk/k-1為狀態一步預測值。正常工作時，卡爾曼濾波殘差服從零均值高斯分布，其方差為：

=E[(yk-Hkxk/k-1)×(yk-Hkxk/k-1)T]

(11)

式中,Pk/k-1為一步預測方差陣；Rk為量測噪聲陣。

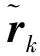
(12)

系統正常工作情況下，βk服從自由度為m的卡方分布，即βk～χ2(m)。通過選擇適當的誤警概率PFA，可得到檢測門限值Td。檢測門限值Td與衛星數n和允許的誤警率PFA有關。

(13)

根據χ2分布的概率密度曲線，設自由度為7，虛警門限PFA=0.01時，組合導航系統卡爾曼濾波卡方檢驗的概率密度函數如圖1所示，可以得到故障檢測門限為15.72。

卡爾曼濾波殘差卡方檢驗法可以有效地對偽距跳變式干擾進行檢測與識別，同時由于各個偽距觀測量相互獨立，在保證系統前一次沒有故障的前提下，還可以有效地對多顆故障進行識別。但是對于偽距緩變式干擾，該方法則無能為力。當系統中存在偽距緩變式干擾時，偽距誤差會影響狀態預報值xk/k-1，狀態預報值會對誤差進行跟蹤，導致有數據融合，濾波器得到的新息值rk較小，無法對其進行故障檢測與識別。表1為故障檢測算法的對比。

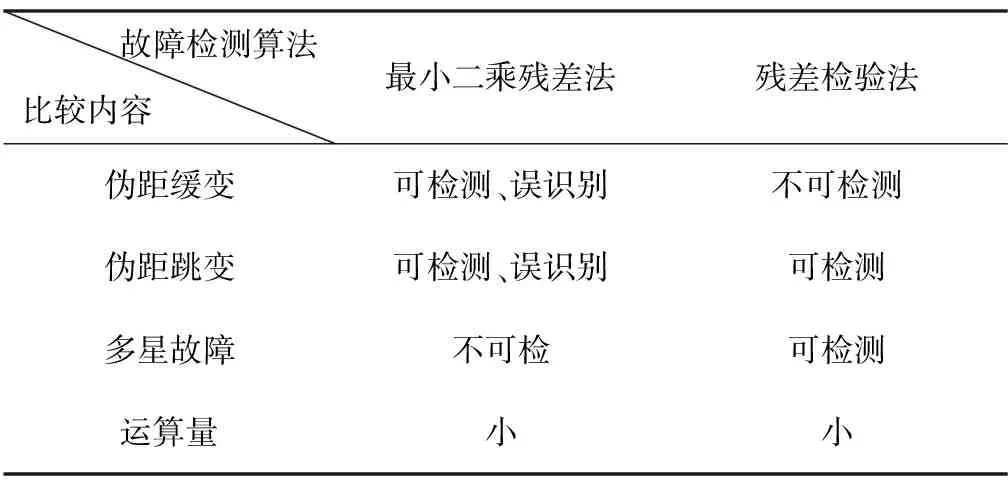
表1 故障檢測算法對比

3 組合導航系統故障檢測和識別算法工程實現研究

3.1 組合導航系統故障檢測和識別算法研究

組合導航系統故障檢測算法是充分利用已有算法的優點，結合緊組合導航系統運行的硬件基礎進行的故障檢測算法，設計了一種能夠在工程上實現的組合導航系統故障檢測和識別算法。故障檢測模塊采用氣壓輔助下的最小二乘殘差法，突變故障識別算法使用卡爾曼濾波殘差卡方檢驗法，保證故障識別的準確可靠；考慮到組合導航系統使用的實時性和硬件限制，基于自主完好性外推法的緩變故障識別方法在本組合導航系統上失去使用意義，當檢出系統存在非突變故障時，組合導航系統切換導航模式，利用慣導系統進行純慣性導航。緊組合導航系統故障檢測算法流程如圖2所示。

根據上文分析，故障檢測模塊中的最小二乘檢測法可以較快地檢測出故障[14]，并且具有檢出突變故障和緩變故障的能力。在故障消除或剔除后能夠及時報出系統無故障信號，不受先驗信息的干擾，實時利用當前時刻的信息進行故障的檢測。所以最小二乘殘差法非常適合作為組合導航系統的故障檢測模塊。缺點是最小二乘殘差法需要5顆星才能檢出故障，6顆及以上才能識別故障。根據第2節的分析，在氣壓高度傳感器的輔助下，最小二乘殘差法在4顆星時就可檢出故障，衛星導航接收機滿足定位條件就能進行故障檢測，極大地提高了組合導航輸出信息的可靠性。突變故障檢出模塊采用卡爾曼濾波器殘差卡方檢驗法，根據卡爾曼濾波器的相關理論，利用卡爾曼濾波器新息構造的故障檢測識別模塊可以實時地識別出具體的衛星故障，從而為故障剔除模塊提供信息。當突變故障檢出某顆衛星存在故障后，則將該衛星剔除，然后繼續進行最小二乘檢測，保證進入數據融合濾波器的信息不存在故障。當檢出非突變故障時，由于組合導航系統不具備剔除緩變故障的能力，為了保證導航信息的可靠性，則退出組合導航，利用慣導系統進行純慣性導航。

3.2 組合導航系統故障檢測和識別算法仿真驗證

根據上文分析，結合組合導航系統常見的偽距突變故障和偽距緩變故障，利用最小二乘算法進行故障檢測，并將最小二乘作為故障檢出和故障消除的標志。利用組合導航系統卡爾曼濾波卡方檢驗識別具體偽距故障的衛星，然后將故障剔除后重新利用最小二乘殘差檢測算法進行故障檢測，直至觀測量中無故障，保證組合導航數據融合濾波器不被故障污染。

1)偽距突變故障檢測和識別

利用組合導航系統實際收星數據進行復現仿真，組合導航系統全程收到7顆導航衛星，故障條件設置如下：

突變故障1，計算次數10～50時，2號衛星偽距跳變100m；

突變故障2，計算次數300～350時，2號衛星偽距跳變200m；

突變故障3，計算次數600～620時，1號衛星偽距跳變20m；

仿真結果如圖3所示。

從圖3中可以看出，當組合導航系統偽距存在突變故障時，組合導航系統在偽距跳變處存在位置誤差較大的情況(50m左右)，由此可見，偽距跳變對組合導航系統的導航定位影響較大。

根據圖4所示，當系統存在仿真條件中設置的3個突變故障時，最小二乘殘差法及時送出檢測故障，并且在突變故障消除后，立刻消除檢測故障，能夠很好地檢出突變故障，并在故障消除后及時報出無故障。

根據圖5仿真結果可知，組合導航系統的卡爾曼濾波殘差卡方檢測在最小二乘殘差法檢出系統存在故障后，利用能夠及時識別出2號衛星存在的2次較大的偽距突變故障和1號星存在1次較小的偽距突變故障。由此可見，卡爾曼濾波殘差卡方檢測能夠及時地識別出具體的衛星偽距突變故障。

2)偽距緩變故障檢測

在1)突變故障檢測和識別的基礎上，在四號衛星上添加緩變故障。

仿真條件設置：

突變故障1，計算次數10～50時，2號衛星偽距跳變100m；

突變故障2，計算次數300～350時，2號衛星偽距跳變200m；

突變故障3，計算次數600～620時，2號衛星偽距跳變20m；

緩變故障1，計算次數400～450時，4號衛星偽距緩變步長1m。

利用某組合導航系統機載試驗數據進行復現仿真，組合導航系統全程收到7顆GPS導航衛星，并按照故障模式進行設置，仿真結果如圖6所示。

從圖6中可以看出，除去在3.1節中分析的對于突變故障的檢出結果，重點關注系統在400～450s的步長為1m的緩變故障，當計算次數為412時，檢測門限為1.189，已經超過檢出故障門限(檢測門限定位0.5，實際使用根據能夠接受的虛警率[15]進行計算得到)；在計算次數為450時，故障消除，檢測門限立刻小于檢出故障門限。可以看出，最小二乘殘差法可以較為及時地檢出系統的緩變故障，并且在緩變故障消除時能夠及時地消除故障標志。

通過圖7中的分析，在計算次數400～450s時的緩變故障，在緊組合導航系統卡爾曼濾波殘差卡方檢驗結果中可以看出，該緩變故障相對于檢出故障門限(檢測門限設為0.5，只保留高位值，檢測門限根據能夠接受的虛警率計算得到)還相差較多，不能夠滿足故障檢出的要求。因此，該方法不具備檢出偽距緩變故障的能力。

經過上文最小二乘殘差檢驗法和卡爾曼濾波殘差卡方檢驗法對突變故障和緩變故障的檢測和識別理論分析及仿真試驗可以看出，最小二乘殘差檢測法對突變故障和緩變故障均有較好的檢測能力，并且在故障消除后能夠迅速消除故障報警。卡爾曼濾波殘差卡方檢驗對于突變故障具有很好的檢測能力，并能夠準確識別故障星，給組合導航系統剔除故障星提供依據；但是該方法不具備對緩變故障的檢測和識別能力，根據故障檢測流程，當組合導航系統最小二乘故障檢測檢測到導航系統存在故障后，組合導航系統卡爾曼濾波殘差卡方檢驗未識別出突變故障，組合導航系統退出組合導航狀態，轉入純慣性導航狀態，當最小二乘故障檢測算法預警消除后，重新進入組合導航狀態。

4 結論

針對現有的快照法故障檢測算法和自主完好性檢測算法進行優缺點分析，并結合組合導航系統外部故障的機理，從偽距跳變和偽距緩變方向入手，提出了一種能夠利用氣壓高度輔助下的最小二乘殘差法檢測偽距跳變和偽距緩變的檢測算法，并利用組合導航系統卡爾曼濾波殘差法識別具體的突變故障算法模塊。當無法完全剔除檢出的故障時，組合導航系統及時切換成純慣性導航狀態，充分利用SINS系統不受干擾的優點，將純慣性導航作為組合導航系統存在故障時的最可靠的導航方式，當存在未能識別的故障時，提高了組合導航系統在發生突變故障和緩變故障時的完好性。