XLPE電纜的高頻電容測量研究

國網鄂州供電公司檢修分公司 楊 英 耿紅杰 胡函武

高頻電容的精確測量是高頻介電特性研究的基礎，但高頻電容在測量中易受等效串聯電感LS及邊緣效應的影響而產生明顯的實驗誤差。本文依據高頻電容的等效電路，提出了精確計算高頻電容的分析方法，并通過實驗驗證了該方法的合理性。

1.引言

聚合物介電特性的測量研究，在近年來興起的 電氣設備絕緣狀態的無損診斷技術探索，局部放電信號在電纜中傳播的衰變特性研究等諸多領域都具有重要的基礎研究意義。而電纜介質復介電常數實部，虛部。因此，獲取電纜樣品精確的電容C值和電導G值是研究電纜介電特性的基礎。但在高頻電場下電容的測量存在較多的影響因素，導致高頻電容的測量結果產生較大的誤差，這對高頻介電特性的研究造成了一定的影響。

本研究中采用阻抗分析儀測量電纜樣品高頻(1M～120MHz)電容C與電導G。在對電容C測量數據處理方面，通過對元件的等效電路進行深入分析，提出L-K法分析處理等效串聯電感LS及邊緣效應等因素對測量結果的影響，計算得到了精確的電容值。

2.實驗樣品及測量結果

圖1為電導G和電容C的測量結果，從圖中可看出，實驗測量電導G的變化趨勢與理論相似，電纜介質的損耗會隨頻率的增大先增大后減小。從圖中可以看出電容C隨頻率的增大輕微減小，隨后電容隨頻率的增大而不斷增大。測量結果明顯與理論預期變化規律相反。

因此，本文需要對電容C測量結果的異常現象予以充分研究和分析。

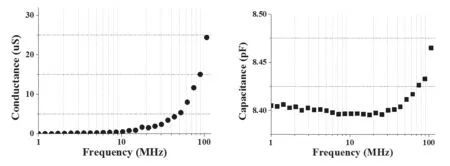
圖1 電導G（左）和電容C（右）測量值隨頻率變化曲線

3.高頻電容測量的中問題及分析方法

高頻電容在測量中會受串聯電感LS的影響而不斷增大，同時由于本實驗中電纜樣品尺寸較短，由邊緣效應引起的附加電容△C不可忽略。因此，本文提出圖2所示的電纜樣品高頻電容測量的等效電路圖。

3.1 高頻電容測量影響因素

3.1.1 等效串聯電感LS的影響

由圖2所示的等效電路圖，可分別得到式(1)和式(2)所示的等效電容Ce，也即電容真實值以及自諧振頻率點f0(SRF)的表達式。

其中，Ce為電容真實值；C電容理論值；其中，△C為附加電容值；ω=2πf 為角頻率；LS為等效串聯電感。

本實驗中樣品電容在pF數量級，芯線電感在nH數量級，可估算高頻段電容測量結果會隨頻率的增大而增大，因此電容測量結果與理論預期相反的變化趨勢，是受樣品導體芯線LS的影響導致的。

3.1.2 邊緣效應的影響

電容測量中由邊緣電場畸變引起的邊緣效應，會使得電容測量結果偏大，本實驗電纜樣品長度較短，由邊緣效應引起的附加電容△C不可忽略。電纜樣品的邊緣效應與樣品邊緣的形狀、電極間距有關，而與樣品的長度關聯性較弱。故本實驗中可認為不同長度電纜樣品的△C相同。

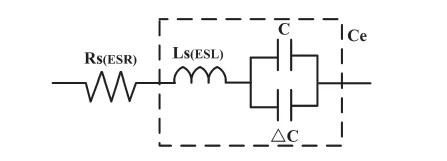
圖2 電容樣品實際等效電路圖

3.2 高頻電容理論分析——L-K法

通過對上述兩點影響因素的分析，本文提出精確計算高頻電容的分析方法——L-K法，消除上述兩因素對電容測量的影響。

長度為l1和l2（其中l1≠l2）的兩樣品的電容理論值C1和C2，等效串聯電感LS1和LS2均與長度成正比。因此，列寫兩樣品電容Ce1和Ce2與其它參數的方程如式(3)所示。

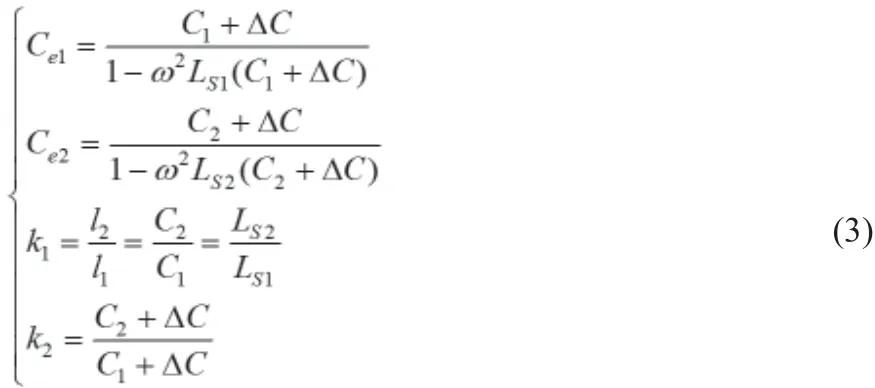
其中，k1為長度比；k2為并聯附加電容△C后總電容的比值。

求解上述各參數關系方程(3)，即可解得式(4)所示LS1及C1及附加電容△C計算公式。

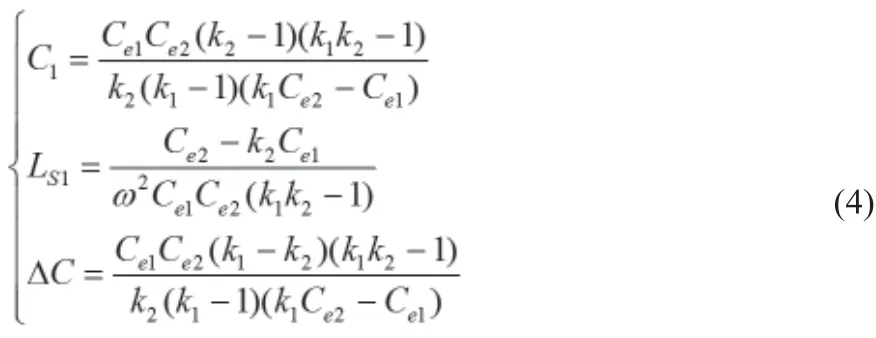
3.3 L-K法實驗數據分析

實驗測量兩個不同長度的樣品的電容值，兩樣品的尺寸規格如表1所示。依據上述理論分析方法，可對測量結果做如下分析。

表1 兩個不同長度樣品的尺寸

由于△C與C成一定的幾何尺寸比例關系，故k2=(C2+△C)/(C1+△C)比值為常數。低頻段(＜1MHz)，根據LS及電容的數量級可估算ω2LS(C+△C)數量級小于10-9。故可按式(1)近似認為Ce≈C+△C，因此可得k2=(C2+△C)/(C1+△C) ≈Ce2/ Ce1。則k2可選取低頻段（如10k～100kHz）兩樣品電容測量值比值的平均值，因此可計算得到k2=1.838。代入式(4)即可求解獲得#1樣品的C1和LS1的計算結果。

圖3為#1樣品電容理論值C1與實驗測量值Ce1的對比曲線。從圖中可以看出，消除誤差影響因素后，電容C1隨頻率的增大而不斷減小，這與介電弛豫理論中偶極子極化在高頻段隨頻率的增大而削弱，使得電容隨頻率增大而減小的預期規律相符。

圖3 電容理論值C1與測量值Ce1對比曲線

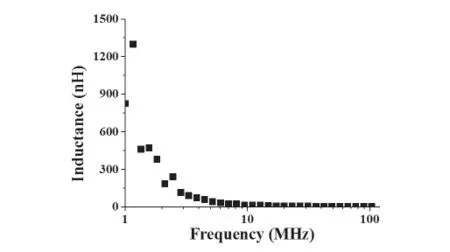
圖4 等效串聯電感LS1的計算值

圖4所示為等效串聯電感LS1的計算曲線，從圖中可以看出，在≤10MHz頻率范圍內，LS1由1MHz處的1300nH減小至10MHz處的15nH，該頻段內LS1數值變化率及波動性較大，這可能是由于電容測量值與真實值間誤差所造成的。

在10M～120MHz范圍內，隨頻率的增大，LS1由10MHz處的15nH與頻率開方呈反比減小至120MHz處的3.5nH，且波動性不斷減小，并趨于平滑。這是由于根據式(4)中LS1計算公式，隨頻率的增大，Ce1和Ce2的測量值與真實值間的誤差對電感計算值的影響將與頻率平方成反比減小，使高頻段LS1的精確度提高，對應高頻段電容理論值C1的有效性大大提高。

4.結論

對不同長度樣品電容值進行測量，并采用L-K法進行處理，根據式(4)可計算得到電容理論值C、等效串聯電感LS以及邊緣效應附加電容值△C。

等效串聯電感LS計算值在較低頻段(≤10MHz)受電容測量值與真實值之間的誤差影響，可能出現一定幅度的波動及數值偏大的現象，但低頻段C的受LS影響較小，此頻段內可忽略LS對電容測量的影響。

在高頻段(＞10MHz)，由電容測量與真實值之間的誤差將成頻率平方比降低，因此LS的計算值具有非常高的精度，故計算得到的電容C也具有較高的有效性。