“一變多控”系統在大型高壓煤磨中的應用

張炳義，劉斯強，馮桂宏

(沈陽工業大學 電氣工程學院，遼寧 沈陽 110870)

0 引 言

相比與傳統的“一變一控”技術而言，“一變多控”技術主要有以下3方面優勢：(1)顯著降低控制系統的成本；(2)可以在一定程度上提高系統的整體效率；(3)電機可以在變頻和工頻間切換運行，可以在不停產的情況下，對設備進行檢修和維護[1-2]。

針對永磁直驅系統“一對一”控制模式不能使系統整體節能效果達到最佳的問題，以一臺1 120 kW，6 kV高壓煤磨樣機為例，本文對永磁直驅電機與“一變多控”控制系統相結合方面的問題進行研究。

1 電機的設計與計算

1.1 電機參數要求

針對現有的生產狀況，用戶給出了具體的電機參數要求，如表1所示。

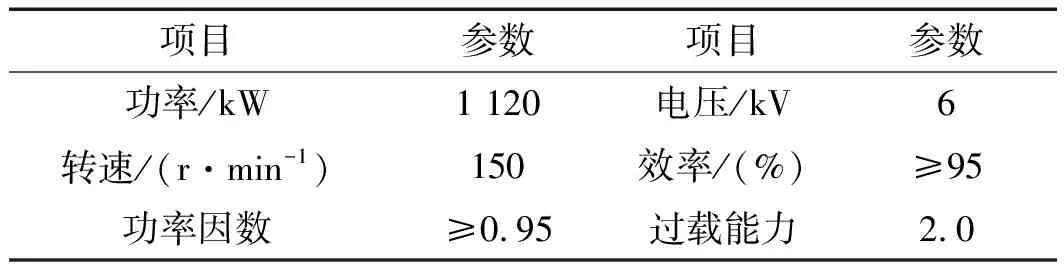
表1 電機參數要求

1.2 電機基本尺寸的確定

電機設計基本尺寸為[3]：

(1)

式中：D—定子內徑；lef—電樞計算長度；αp—計算極弧系數，這里按0.8～0.85選取；KNm—氣隙磁場波形系數，當氣隙磁場分布接近正弦時等于1.11；Kdp—繞組因數；ABδ—兩者乘積為電磁負荷。

整機額定轉矩為71 000 Nm；冷卻方式為水冷。依據永磁電機設計經驗，其中線符合A選取范圍700 A/cm～800 A/cm；氣隙磁密選取范圍0.75 T～0.85 T。且用戶在安裝尺寸上也提出了明確的要求，軸向長度不得長于1.5 m，徑向尺寸在4 m×4 m以內。

確定的電機基本尺寸與參數如表2所示。

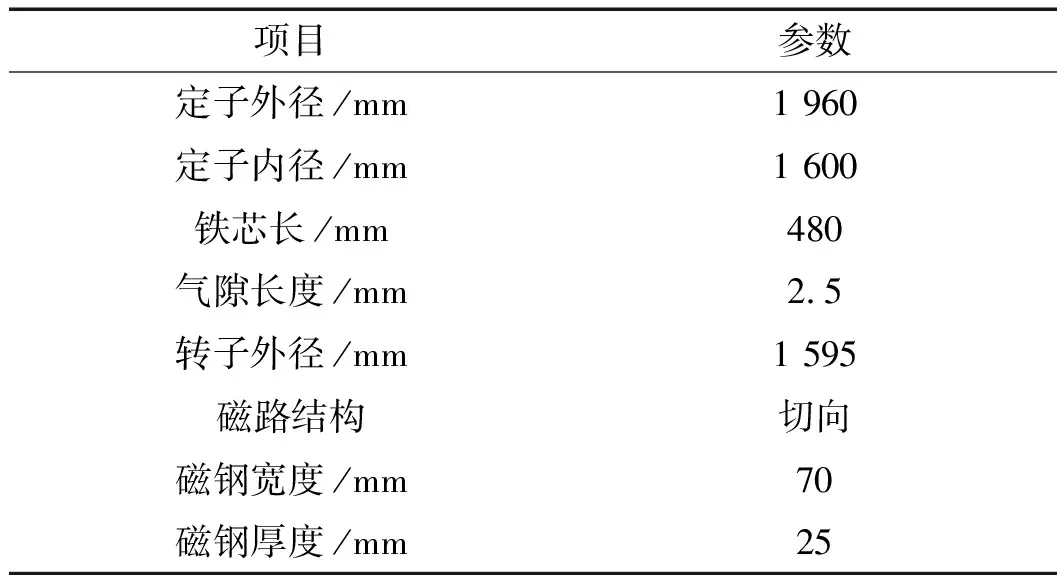
表2 電機基本尺寸參數

1.3 電機極頻比與極槽配合的選擇

根據n=60f/p，考慮到“一變多控”的控制方式，電機額定頻率選為工頻50 Hz，電機極數確定為40。不同的極槽配合對繞組與電機參數的影響，如表3所示[4]。

由電機原理可知：電機繞組中的感應電動勢E=4.44fNΦKdq，要產生一個繞組因數大小的削弱。因此，在極槽配合的選擇上，盡可能使繞組因數大些。這樣，在保證反電勢的基礎上，可以最大程度地降低電機自身成本。

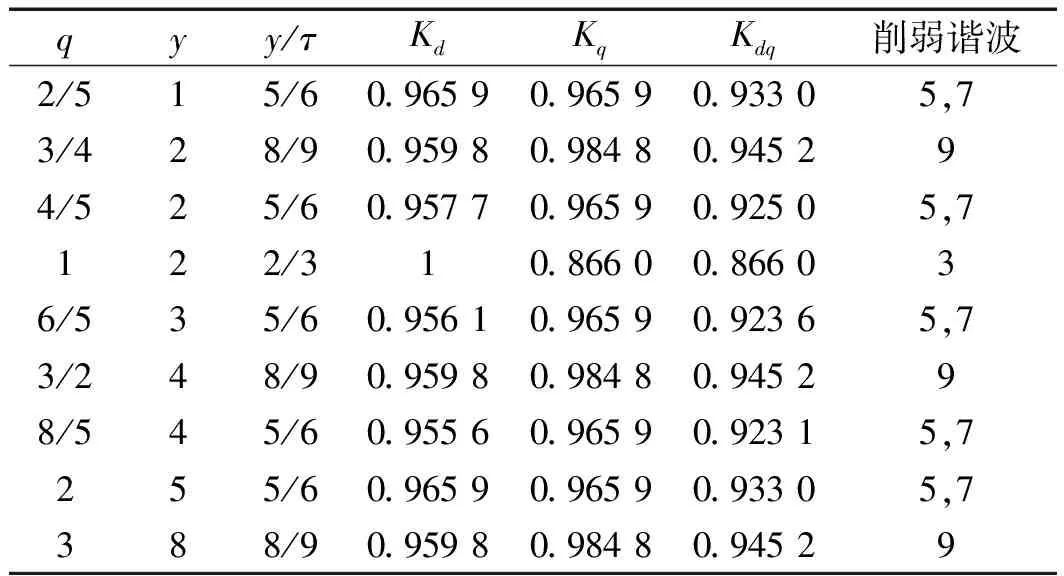
表3 不同極槽配合繞組各系數和諧波削弱情況

Kd—繞組短距系數；Kq—繞組分布系數；Kdq—繞組因數

正常情況下，高次諧波電動勢對相電動勢大小的影響很小，主要影響電動勢的波形。電機中對波形起主要影響作用的為3、5、7次諧波，其中3次諧波，可通過對稱繞組直接消除，而5、7次諧波，則需要采用短距繞組消除。

綜合考慮以上兩方面問題，以及電機的具體尺寸參數，初選兩種極槽配合方式：q=0.8和q=1.2。

1.4 電機計算與仿真

電機計算采用場路結合的方式，路算用于輔助快速設計電機參數，場算對電機參數進行校核與精確計算。

1.4.1 電機磁路法計算

在目前許多工程問題中，電機的磁路法計算仍采用“場化路”的方法。這種方法可以大大減少計算時間，在方案估算、初始方案設計和比較時更為實用。

本文中路算部分，基于經典的電機路算方法，采用了Matlab編程，輔助電機的設計工作。針對工作于恒轉矩區的凸極永磁電機而言，且冷卻方式為水冷。在磁路計算上，參考以往的設計經驗，主要參數應符合以下條件：

(1)空載相反電勢，有效值應為額定相電壓的90%～95%；

(2)凸極率(交軸電抗/直軸電抗)，范圍大致為1.5～2；

(3)銅耗與鐵耗，為了達到電機效率的最優狀態，銅耗與鐵耗盡可能相等，且銅耗略高于鐵耗；

(4)電密與熱負荷，考慮到高壓電機繞組絕緣的絕緣溫度問題以及電機冷卻方式，電密通常選取低于6 A/cm，熱負荷通常選取范圍為1 500 A2(cm·mm2)～1 600 A2(cm·mm2)。

路算結果的部分參數如表4所示。

表4 電機路算部分主要參數

1.4.2 電機有限元法計算

1.4.2.1 空載反電勢的分析

空載反電勢E0是永磁電機重要參數，E0由電動機中永磁體產生的空載氣隙基波磁通在電樞繞組中感應產生，空載反電勢為：

(2)

式中：bm0—永磁體空載工作點；Am—永磁體充磁方向截面積；Br—氣隙磁密基波有效值；σ0—空載漏磁因數。

E0的大小不僅決定電動機是運行于增磁狀態還是去磁狀態，而且對電動機的動、穩態性能有很大影響。其中，對電機溫升、電磁轉矩的穩定性尤為明顯[5]。

在工程上，針對工作于恒轉矩區的電機而言，其空載反電勢數值在額定相電壓的90%～95%之間，其波形應盡可能接近標準正弦波。

q=0.8和q=1.2時的空載相反電勢波形如圖1所示。

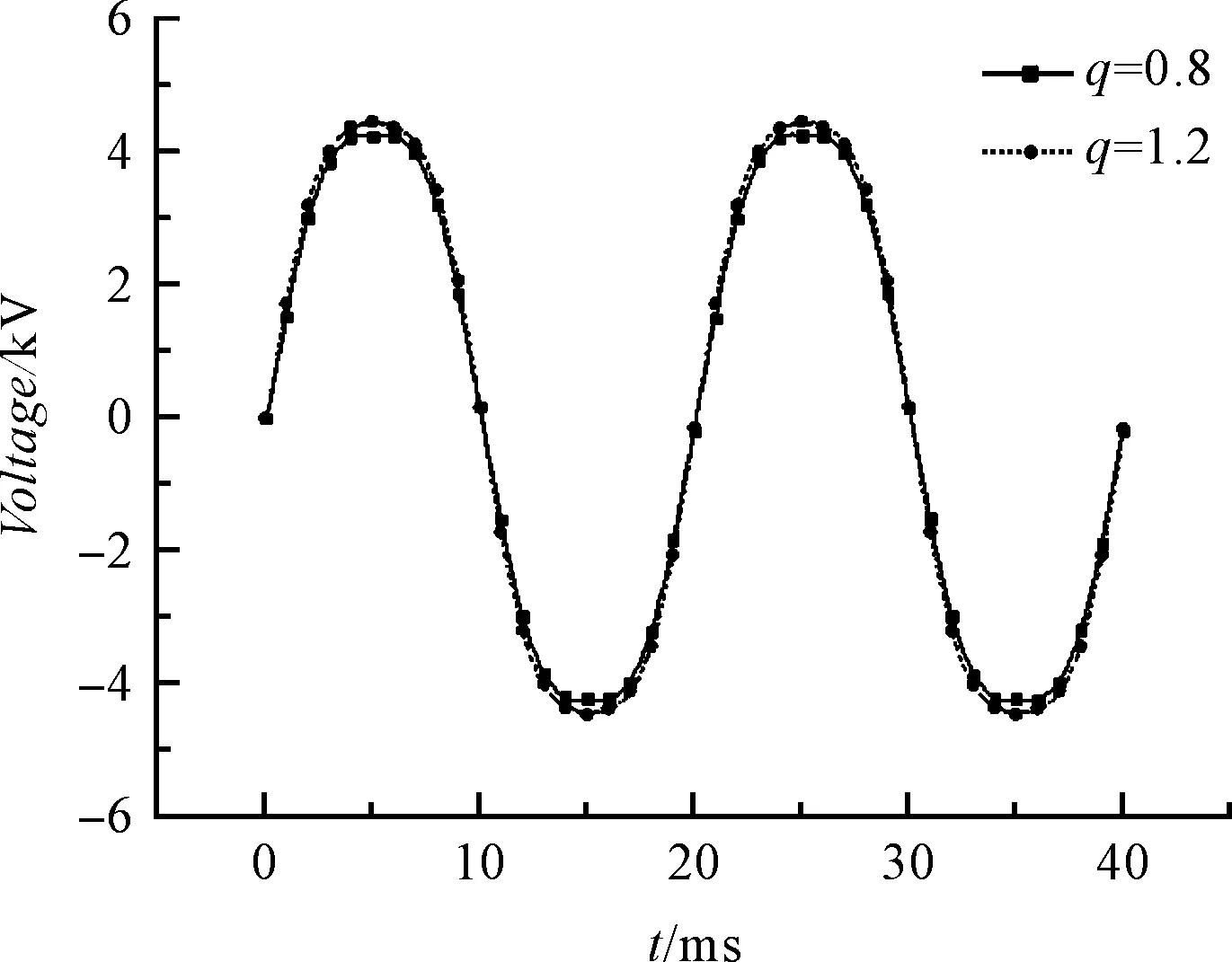
圖1 q=0.8和q=1.2時的空載相反電勢波形

二者的諧波含量對比如表5所示。

表5 二者諧波含量對比

在電機基本尺寸、磁鋼尺寸和繞組完全相同的情況下，當q=0.8時，其空載反電勢有效值為3 300 V；q=1.2時，其反電勢有效值為3 400 V，后者的反電勢有效值略高于前者，但是均處于合理的空載反電勢范圍之內。

從諧波來看，q=1.2時的3次、5次反電勢諧波分量要低于q=0.8的情況，這說明與q=0.8相比，q=1.2時其反電勢波形質量更高，波形更加接近標準正弦波。

1.4.2.2 徑向氣隙磁密的分析

永磁同步電動機的空載氣隙磁密波形基本上為一平頂波，與感應電動機的氣隙磁密波形相差很大，而與直流電機的空載氣隙磁密波形相似。q=0.8和q=1.2時的徑向氣隙磁密波形如圖2所示。

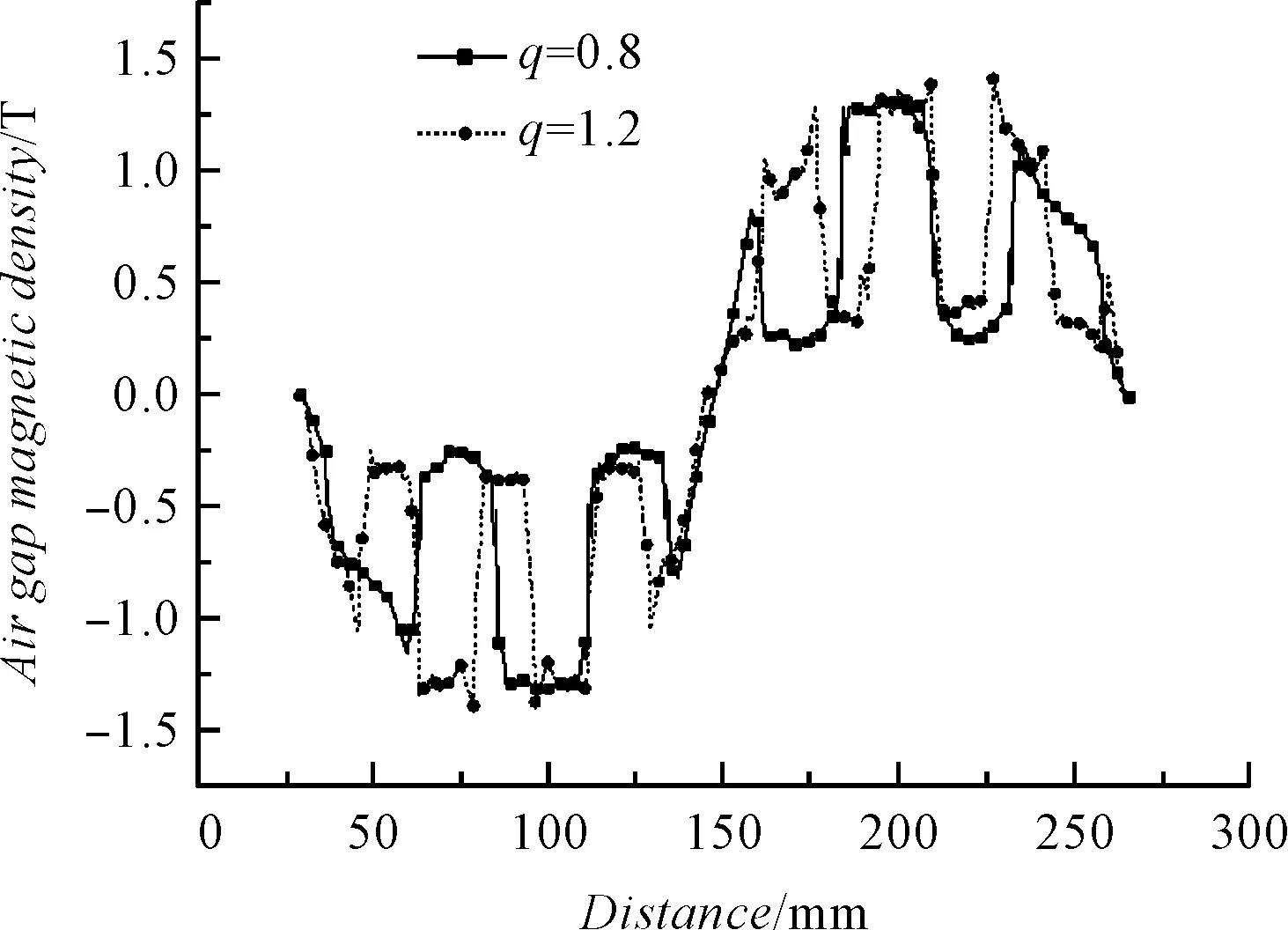
圖2 q=0.8和q=1.2時徑向氣隙磁密波形

二者的諧波對比如表6所示。

表6 二者諧波含量對比

分析比較q=0.8和q=1.2時的徑向氣隙磁密波形與諧波分析，可以得到以下結果。

(1)當q=1.2時，其徑向氣隙磁密的基波幅值要高于q=0.8的情況；

(2)當q=0.8時，此時對于徑向氣隙磁密中的3次和7次諧波的削弱，要優于q=1.2的情況；

(3)當q=1.2時，此時對于徑向氣隙磁密中5次，以及7次以上高次諧波的削弱，要優于q=0.8的情況。

1.4.2.3 空載齒槽轉矩的分析

齒槽轉矩是由永磁體與電樞齒之間相互作用力的切向分量引起的，空載齒槽轉矩表達式為：

(3)

式中：La—電樞鐵芯的軸向長度；R1，R2—電樞外半徑和定子軛內半徑;N—使nz/zp為整數的整數。

由于齒槽轉矩是由于電樞開槽引起的，則槽口越大，齒槽轉矩也越大；并且對電樞而言，齒寬槽寬比為1是合適的。

q=0.8和q=1.2時的齒槽轉矩波形如圖3所示。

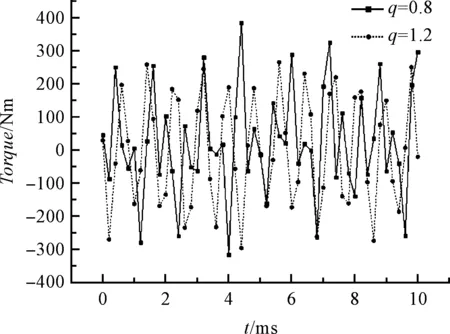
圖3 q=0.8和q=1.2時齒槽轉矩波形

比較q=0.8和q=1.2時的齒槽轉矩波形可知：當q=0.8時，其齒槽轉矩峰值為385 Nm，平均值為18.7 Nm；當q=1.2時，其齒槽轉矩峰值為282 Nm，平均值為3.7 Nm。顯然，當q=1.2時，電機的齒槽轉矩得到了顯著的削弱。

1.4.2.4 空載齒磁密的分析

對于低速大扭矩電機而言，通常為了保證定子的強度足夠大，定子軛部厚度通常與定子槽深成1∶1的關系，那么在磁路角度上而言，定子軛部余量是非常大的，定子軛部的磁密通常遠遠低于定子齒磁密。由電機學原理可知：pFe∝B2f1.3。因此，就低速大扭矩電機而言，定子鐵耗主要產生于定子齒部，定子發熱過程主要也發生在定子齒部分。

工程上，為了充分利用硅鋼片，同時也為抑制定子齒部發熱，所以在空載狀態下，就DW470-50沖片而言，定子齒磁密通常取在1.7 T以下。

q=0.8和q=1.2時定子齒高度1/3處磁密隨時間變化曲線如圖4所示。

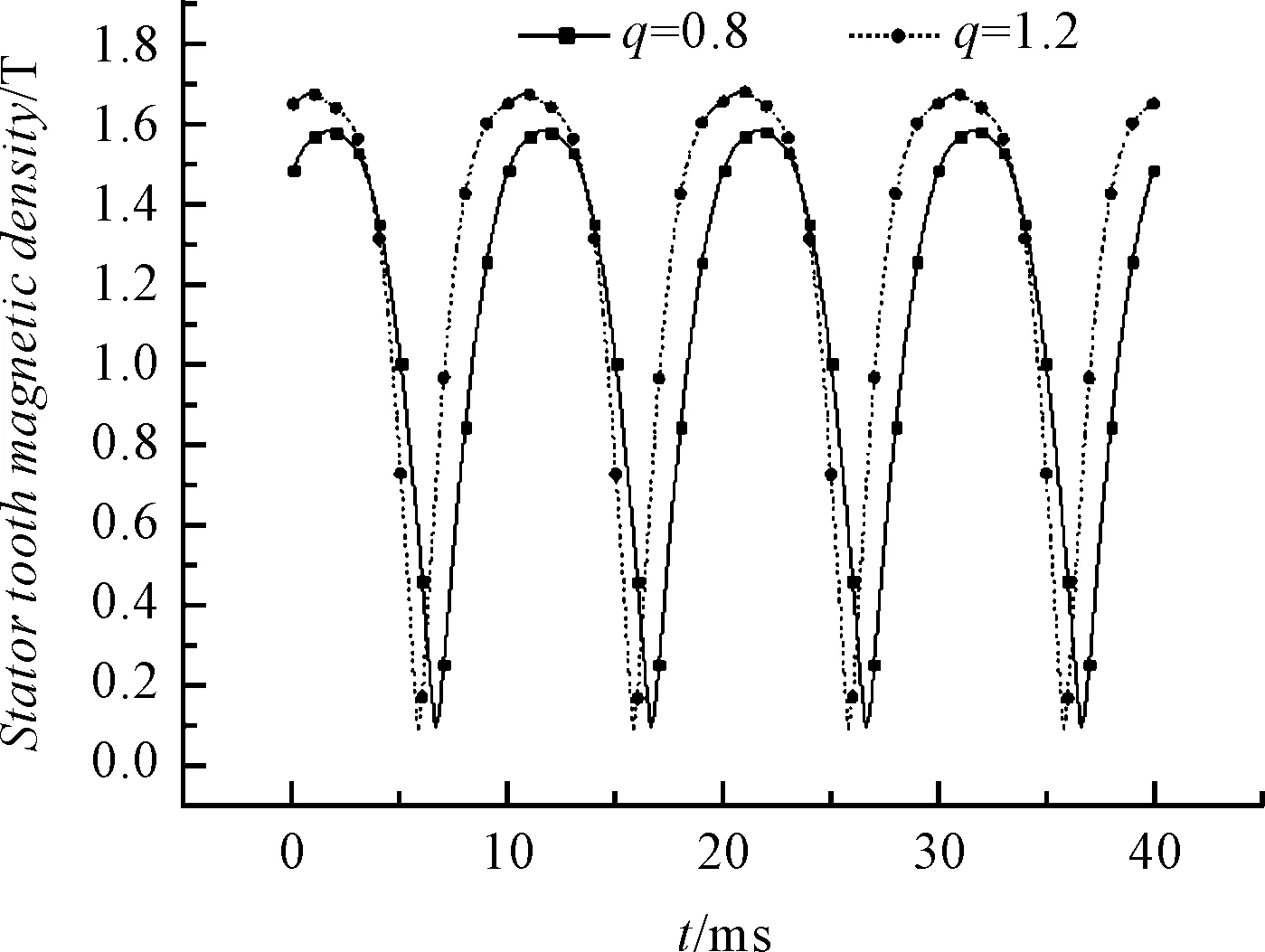
圖4 定子齒高度1/3處磁密隨時間變化曲線

為了方便確定定子齒上某點齒磁密的峰值，本研究對定子齒磁密隨時間的變化規律取絕對值。

通過以上的分析，針對定子齒磁密可以得到：

(1)定子齒磁密隨時間基本呈正弦規律變化；

(2)q=0.8時，定子齒磁密峰值為1.588 T，q=1.2時，定子齒磁密峰值為1.687 T。在滿足定子齒磁密要求的基礎上，q=0.8時，齒磁密明顯偏低，這對于鐵芯材料的利用是不利的。

1.4.2.5 電磁轉矩分析

永磁電機的電磁轉矩由兩部分構成：(1)由定子交軸電流與永磁體磁鏈相互作用產生的永磁轉矩Tm；(2)由于轉子磁路不對稱所產生的磁阻轉矩Tr。

永磁電機總的電磁轉矩可表達為：

(4)

式中：ω—角頻率,ω=2πf;e0—空載反電勢有效值;id—直軸電流有效值;iq—交軸電流有效值;Xd—直軸電抗;Xq—交軸電抗。

本文設計的電機轉子結構采用切向結構，其交軸電抗Xq要明顯的大于直軸電抗Xd，且永磁機正常工作均處去磁狀態id<0。由上述表達式可知，此時，磁阻轉矩為一驅動性質的轉矩，有助于提升電機負載能力[6]。

q=0.8和q=1.2時，在額定電流激勵下的電磁轉矩波形如圖5所示。

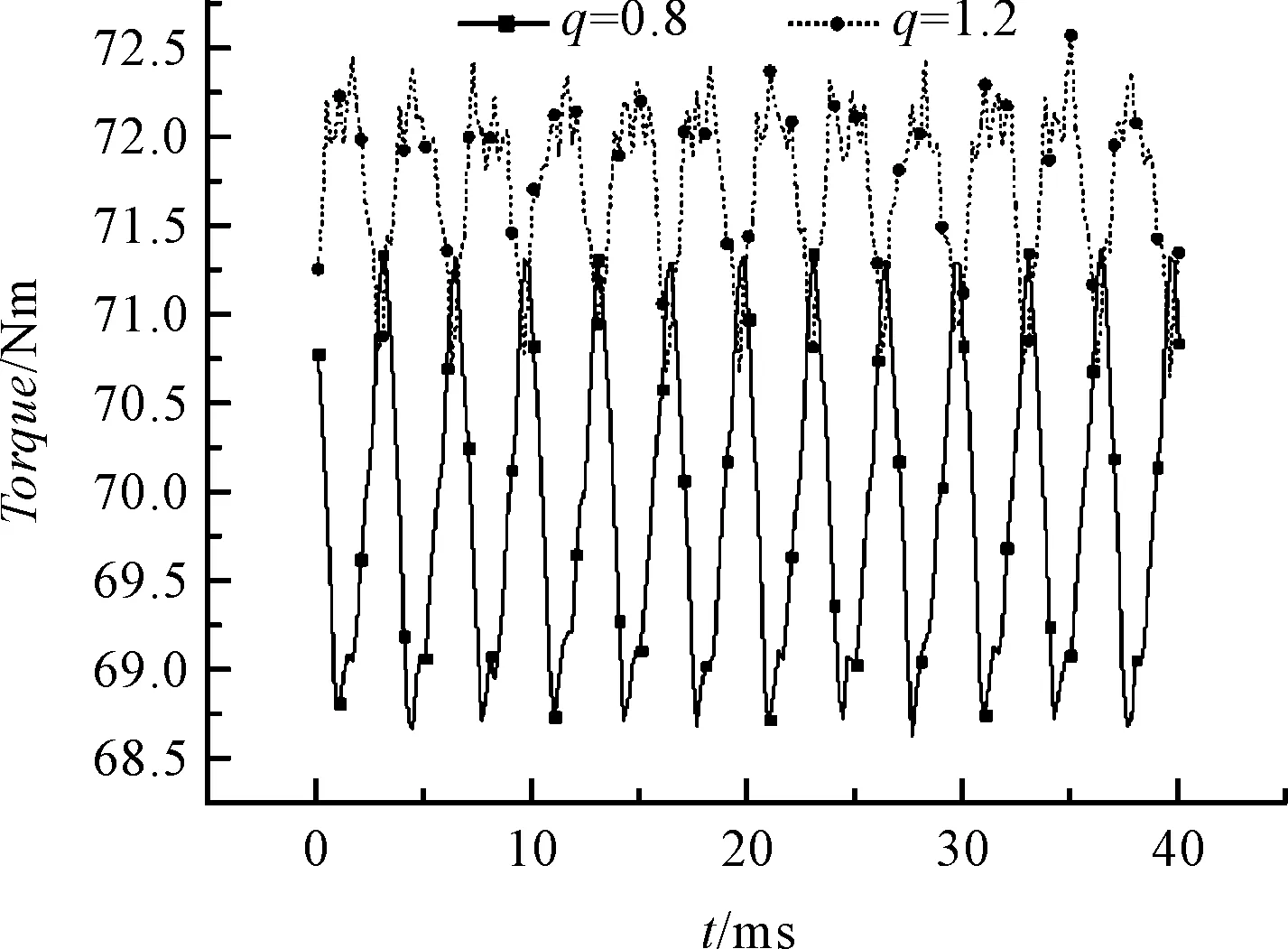
圖5 q=0.8和q=1.2時額定電流下電磁轉矩波形

通過以上的仿真分析可知：對于給定的額定電流激勵而言，當q=0.8時，其轉矩的平均值為69.9 kNm；而q=1.2時，其轉矩平均值為71.7 kNm。顯然，在額定電流條件下，q=1.2的電磁轉矩特性要優于q=0.8。

1.4.2.6 負載磁密分析

為了滿足電機性價比最佳的設計，通常電機的工作點選擇在硅鋼片的膝點附近，對于DW470-50而言，其膝點對應磁密大致在1.9 T左右，因此，在針對電機額定負載設計時，定子齒部的磁密需要合理的設計于校核。

q=0.8和q=1.2時定子齒高度1/3處磁密隨時間變化曲線如圖6所示。

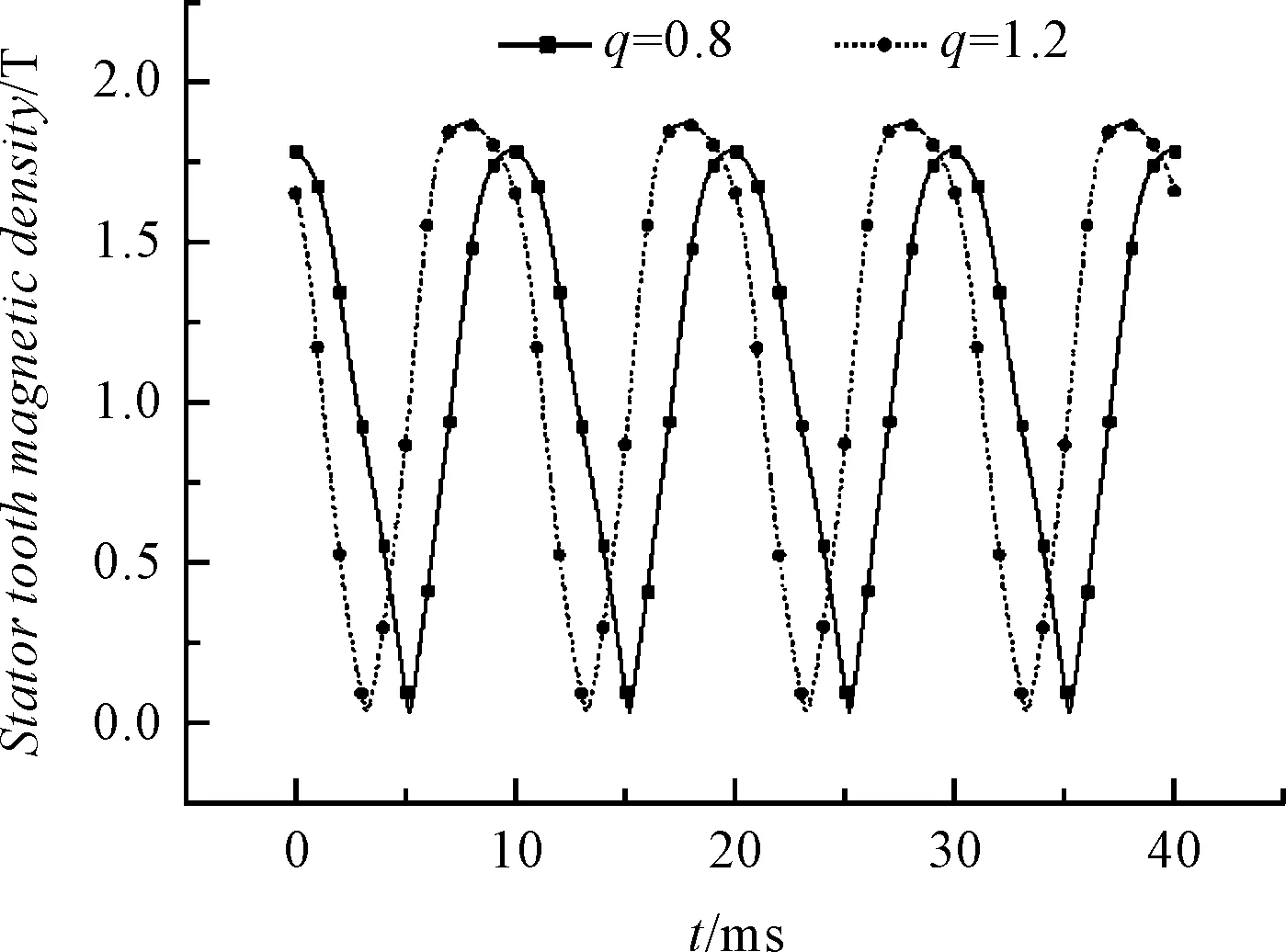
圖6 定子齒高度1/3處磁密隨時間變化曲線

理論上永磁電機在負載情況下，d軸與q軸的交叉飽和，會對氣隙磁密的波形造成一定影響。其d軸電樞反應的增磁或去磁作用，會對電機氣隙磁密的幅值造成影響，而q軸電樞反應，會使氣隙磁密波形發生畸變。

分析q=0.8和q=1.2時的定子齒磁密波形可知：當q=0.8時，定子齒磁密幅值為1.79 T，其波形仍然接近正弦，這說明交叉飽和的影響很小，工作點遠未達到硅鋼片的膝點；當q=1.2時，定子齒磁密幅值為1.87 T，波形已經發生了明顯的畸變，此時已經出現了較明顯的交叉飽和現象，工作點已接近硅鋼片的膝點附近。顯然，從硅鋼片利用率的角度，q=1.2的設計方案要優于q=0.8的設計方案。

1.5 電機電磁方案的確定

電機電磁方案的最終確定，要考慮兩方面因素：(1)電磁設計是否合理；(2)工藝上是否便于加工。

通過比較以上的電磁計算與分析結果可知，在q=0.8與q=1.2，兩者的電磁計算結果，雖各有優劣，但是其差別均在可接受的范圍內。

在工藝方面，由于電機繞組部分采用了成型繞組，因此在繞組制作上二者存在一定差別。首先，由計算短距繞組截距，針對q=0.8和q=1.2而言，其截距y均為102.44 mm，這屬于典型的小跨距成型繞組。其次，q=0.8和q=1.2的方案中，成型繞組均采用了2根并繞方式。q=0.8時，由于定子槽較寬，銅排采用了5.6 mm×3.15 mm的規格；q=1.2時，定子槽較窄，銅排采用了4.5 mm×3.0 mm規格。由于q=0.8時，銅排截面積較大，在繞組拉形后，出現了嚴重的回彈，并且繞組難以整形；而采用q=1.2時，銅排截面積縮小，對于繞組拉形以及繞組整體整形都相對容易。

綜合考慮以上兩點因素，最終確定采用q=1.2的極槽配合方式。

1.6 樣機試驗驗證

針對以上方案，本文進行了樣機裝配，并進行了相應實驗。實測電機空載相反電勢為3 314 V，與設計值3 400 V相差不大。

實測的空載反電勢波形如圖7所示。

圖7 實測A相空載反電勢波形

2 變頻切工頻控制器的設計

2.1 控制器的選型

對于長時工作制，并且工作在恒轉矩區的電機，永磁電機適配變頻器的選型以額定電流為依據，且變頻器輸出電流要大于電機的實際工作電流。

出于系列化的考慮，本文中的樣機功率范圍1 120 kW～1 400 kW，當系列電機達到最高功率時，其額定電流計算值為142 A。因此，變頻器考慮到通用性以及一些可能出現的過載情況。

變頻器的選型如表7所示。

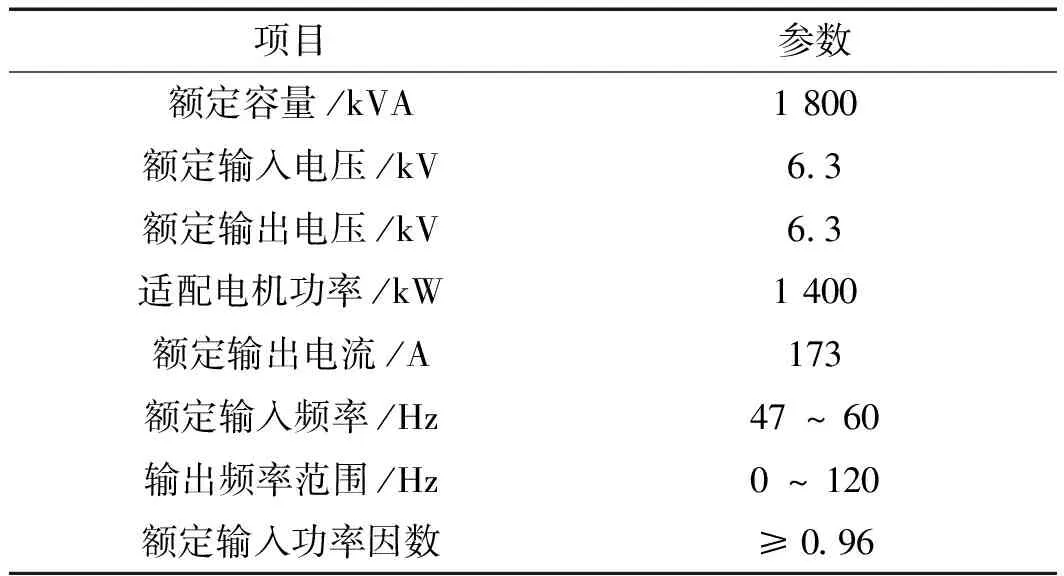
表7 變頻器選型數據

2.2 控制策略的選取

本文樣機為一臺大型煤磨專用，屬于節能改造系列方案，故其要求電機的效率盡可能高，并且長時工作負載率在70%～80%，電機工作在恒轉矩區。

控制策略選擇為“最大轉矩電流比”控制[7]。

滿足“最大轉矩電流比”的定子電流控制圖如圖8所示。

圖8 定子電流控制圖

由電壓極限橢圓以標幺值表示的電壓方程為：

(5)

同樣可以得到標幺值形式的功率方程和轉矩方程：

Pe=ωr[e0iq+(1-p)xdidiq]

(6)

Te=Pn[e0iq+(1-p)xdidiq]

(7)

式中：ρ—凸極率，ρ=xq/xd。

在圖8中，“最大轉矩電流比”軌跡Ⅰ與電壓極限橢圓相交于A點。顯然，應控制定子電流矢量is不超過OA的范圍(圖中O為原點)。

式(7)可改寫為：

(8)

通過對上式求極小值，可得滿足最大轉矩/電流比的定子電流矢量is的空間相位式：

(9)

于是有：

id=|is|cosβ

(10)

iq=|is|sinβ

(11)

圖8中，落在電流極限圓內的Ⅰ軌跡OA線段，這表示電動機可在此段軌跡的每一點上做恒轉矩運行，而與通過該點的電壓極限橢圓對應的速度就是轉折速度。恒轉矩值越高，電壓極限橢圓的半徑越大，對應的轉折速度越低。其中，A點與最大轉矩輸出對應，其轉折速度利用標幺值可表示為：

(12)

將式(10，11)代入式(12)，可得：

(13)

由以上分析可知：采用“最大轉矩電流比”控制模式，當電機工作于額定轉矩狀態下，其凸極率、額定電流、直軸去磁電流和交軸轉矩電流基本不再發生變化或變化幅度很小，此時，就變頻器而言，轉折速度僅僅取決于電機定子電壓矢量us的最大值[8]。就本研究中的樣機而言，其工作狀態幾乎均在恒轉矩區，因此對于轉折速度的選取，可以選擇在額定轉速稍高的位置。

2.3 切換功能的實現

樣機由變頻運行，切入工頻運行的過程，可以參考發電機并網運行的過程[9]。當同步發電機并聯投入電網時，需要滿足5點條件：(1)波形相同；(2)頻率相同；(3)幅值相同；(4)相位相同；(5)相序相同。前4點是交流電磁量恒等的基本條件，最后一點是多相系統相容的基本要求。

但是在實際切換過程中，以上5點條件很難同時達到。因此，實際切換時前4點條件允許稍有出入，但是第5個條件必須絕對滿足。因為發電機并網時，客觀上同相之間的電壓差和相位差是不可避免的，發電機沒并網之前自己算作一個獨立的電力系統，外部電網算作另外一個獨立的電力系統，兩個獨立系統并聯運行前需要投同期，同期考慮3個問題，即電壓差、相位差、頻率差，理論上3者差為0時，即為最佳同期點，實際上這是幾乎不可能達到的。所以，只需要電壓差、相位差和頻率差在一個允許的范圍內即可給出并網信號，使電機組安全可靠運行。差越小，沖擊電流越小，需要系統無功功率也最小，對外部匹配電網的影響也就越小。

當變頻器切工頻時，變頻調速系統會調整輸出電壓的相位、頻率和幅值，當其與工頻電源一致時，切換到工頻運行，盡可能或消除沖擊；當工頻切換變頻運行時，變頻調速系統會自動追蹤當前電機的轉速，然后切換到變頻運行。同步切換功能通過切換柜自動實現，對電機沖擊小，運行可靠，可以實現“一變多控”。

變頻切工頻流程：設置同步切換使能有效，變頻調速系統運行到50 Hz，然后給出變頻切換工頻命令，變頻調速系統開始鎖相，鎖相成功后變頻調速系統的切換開關動作，切入到工頻電網運行。

工頻切變頻流程：變頻調速系統工頻運行，下發工頻切換命令，電機與工頻電網脫離，變頻調速系統追蹤電機當前轉速和運行方向，然后加速到變頻目標頻率運行。

變頻切工頻具體流程如圖9所示。切換線路的連接如圖10所示。

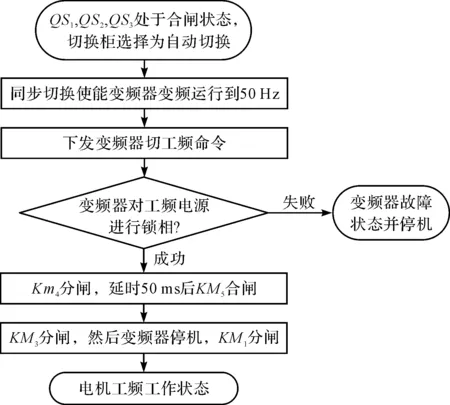
圖9 變頻切工頻流程圖

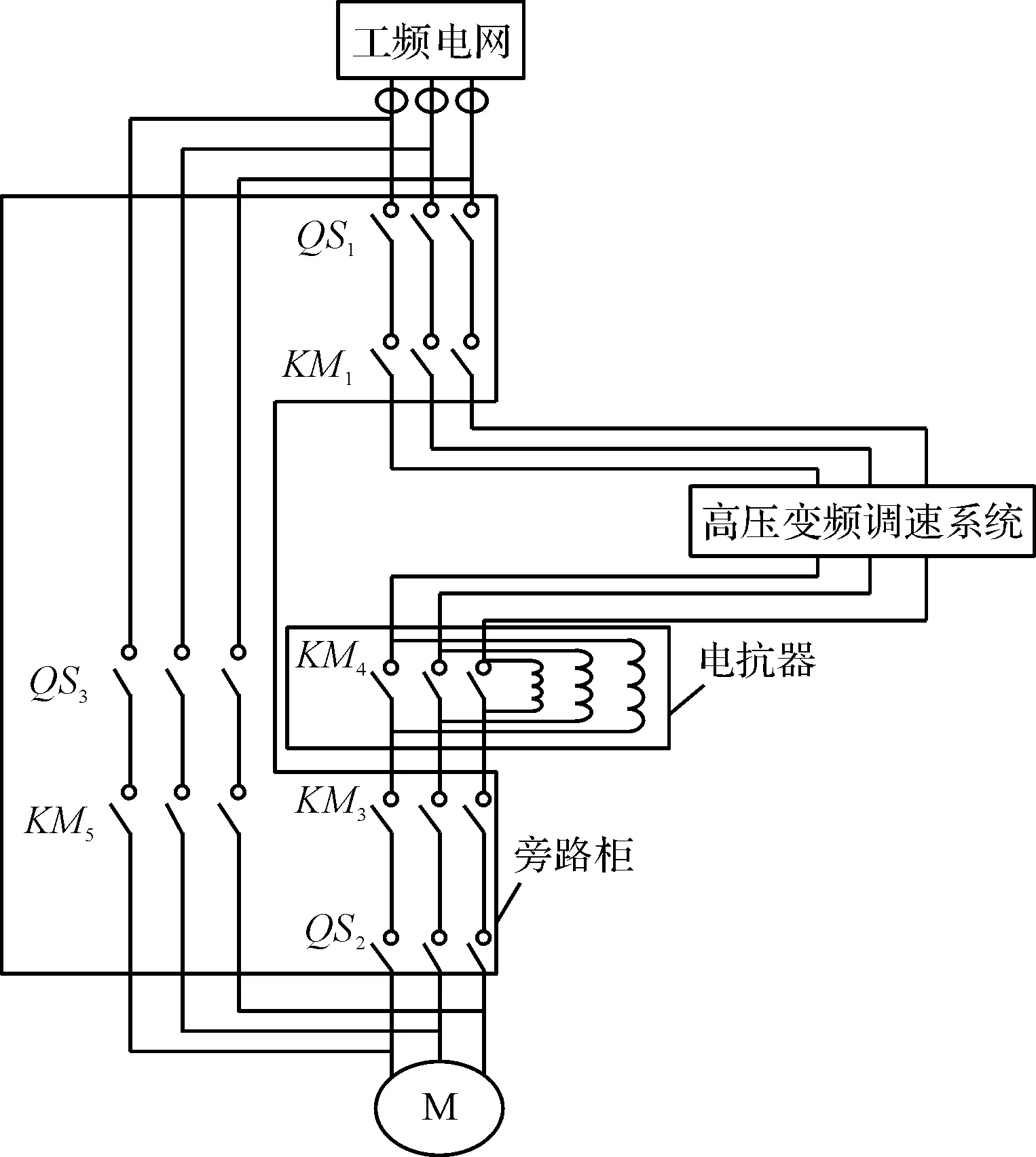
圖10 同步切換線路圖

2.4 樣機試驗驗證

針對上述切換系統的可行性，本研究進行了樣機組裝，并進行了相應的試驗驗證。

結合電機和該套控制系統，本研究進行了相應的變頻-工頻切換試驗。切換過程中，變頻調速系統監測到的電機三相電流波形和三相電壓波形分別如圖(11，12)所示。

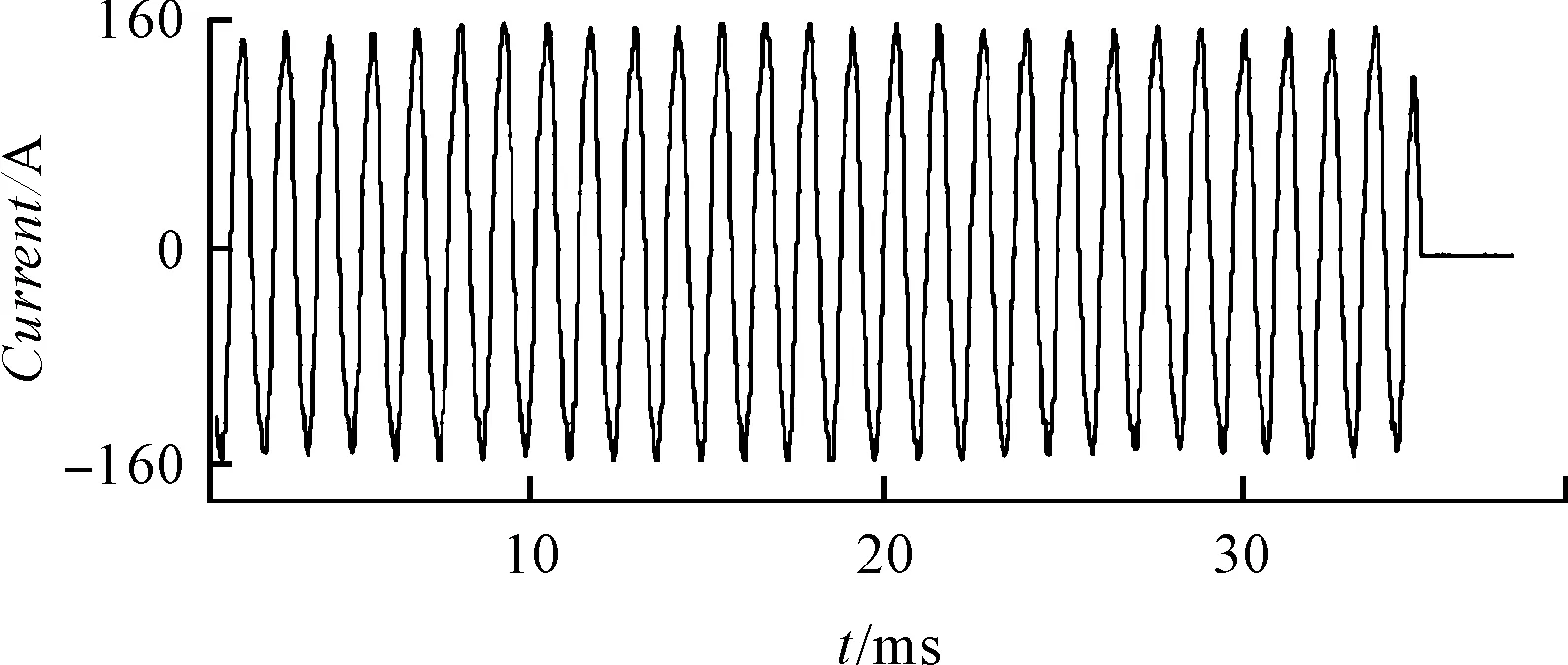
圖11 切換過程中的A相電流波形

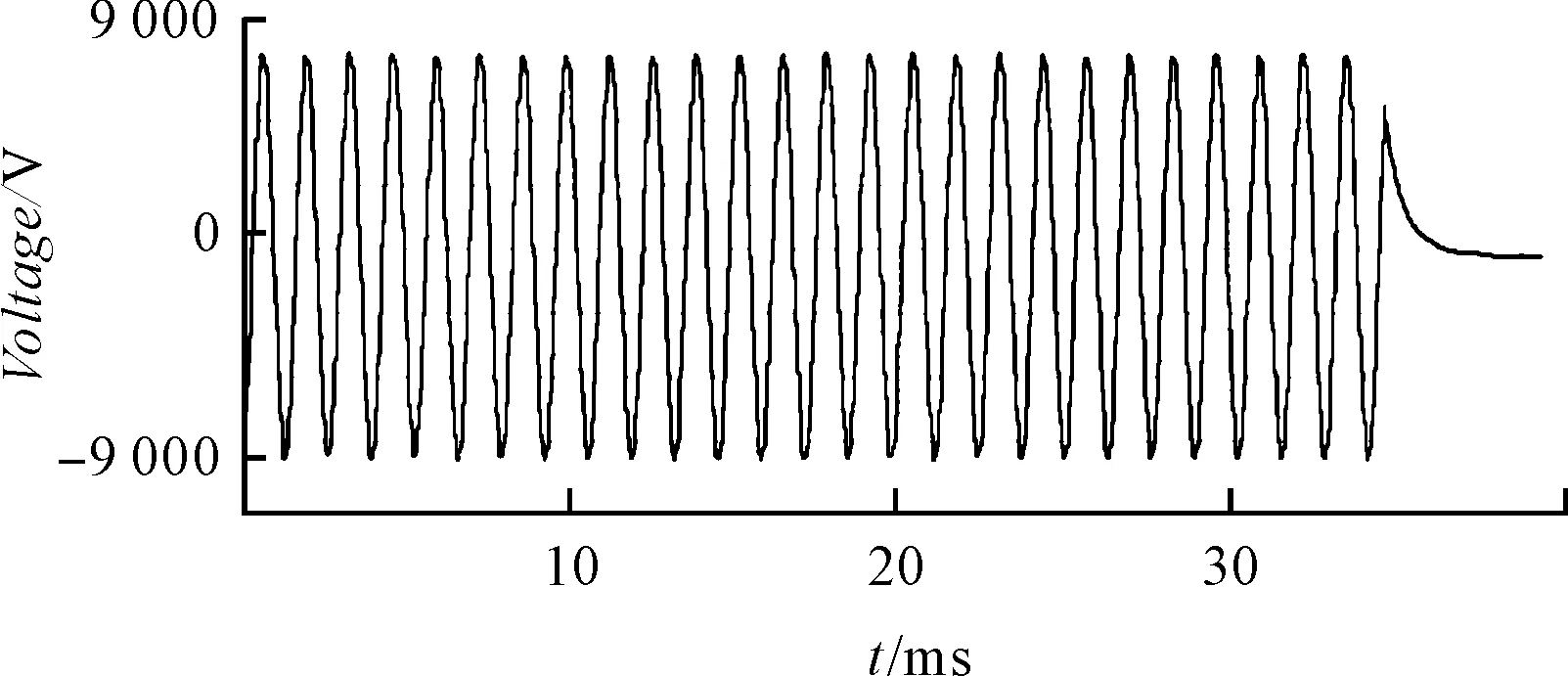
圖12 切換過程中的A相電壓波形

通過比較波形的趨勢可以看出：在由變頻向工頻切換過程中，無論是電流還是電壓，均未出現沖擊現象，切換過程平滑。且切換后，電機并未發生噪聲和跳動現象。說明切換過程基本成功，不會對電網和電機造成沖擊。

3 結束語

本文以一臺1 120 kW，6 kV高壓低速大扭矩煤磨為例，著重研究了“一變多控”系統中電機與切換系統的設計問題，并得到如下結論：

(1)對于低速大扭矩電機來說，采用多極，分數槽繞組可以顯著優化電機整體性能；

(2)由于高壓電機繞組均為成型繞組，尤其針對小跨距成型繞組而言，其工藝性為一個重要的考慮方向，在保證電機性能的基礎上，可將q取的略大些，這樣可減小銅排的截面積，便于加工；

(3)針對于變頻切工頻時切換回路與控制流程的設計，通過實驗結果可看出在切換中電壓、電流基本無明顯沖擊，電機可以平穩地由變頻切換為工頻狀態。