用樣本估計總體的六種題型

文 /李培華

樣本在一定程度上反映總體，能對總體作出估計和推測.用樣本估計總體是統計學的基本思想.中考的常見類型有以下六種.

類型1 估計總體的數量

例1為了估計池塘里有多少條魚，從池塘里捕撈了1000條魚做上標記，然后放回池塘里，經過一段時間，等有標記的魚完全混合于魚群以后，再捕撈200條，若其中有標記的魚有10條，則估計池塘里有魚______條．

填20 000．

類型2 直接求樣本的數量

例2某市對九年級學生進行“綜合素質”評價，評價結果分為A，B，C，D，E五個等級.現隨機抽取500名學生的評價結果作為樣本進行分析，繪制了如圖1所示的統計圖.已知圖1中從左到右的五個長方形的高之比為2∶3∶3∶1∶1，據此估算該市80 000名九年級學生中“綜合素質”評價結果為A的學生約為______人．

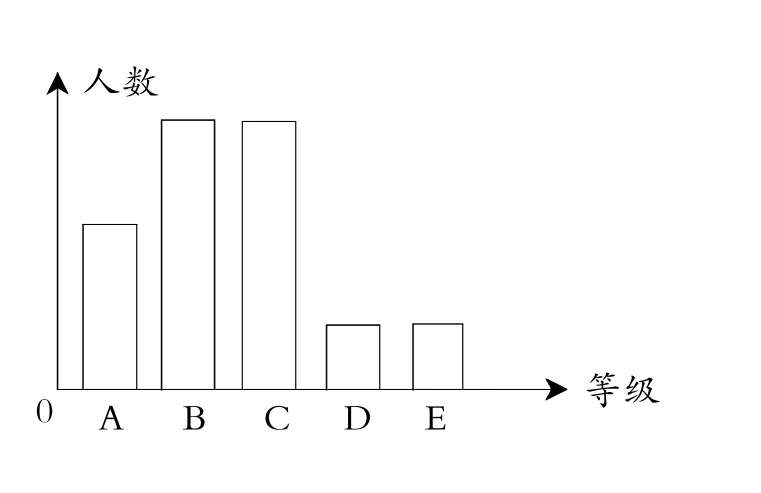
圖1

解：該市80 000名九年級學生中“綜合素質”評價結果為A的學生約為

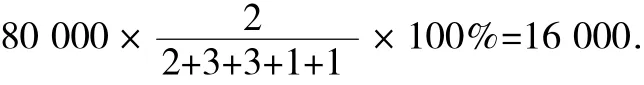
答案為16 000.

類型3 間接求樣本的數量

例3某商店進行“迎五一，大促銷”摸獎活動，凡是有購物小票的顧客均可摸球一次，摸到的是白球即可獲獎．規則如下：一個不透明的袋子中裝有10個黑球和若干個白球，它們除顏色不同外，其余均相同，從袋子中隨機摸出一個球，記下顏色，再把它放回袋子中搖勻，重復此過程．共有300人摸球，其中獲獎的共有180人，由此估計袋子中白球大約有_____個.

解：設袋子中白球有x個.

解得x=15.

經檢驗，x=15是分式方程的解.袋子中白球大約有15個.

填15．

類型4 估算樣本的加權平均數

例4老王的魚塘里年初養了某種魚2000條，到年底捕撈出售，為了估計魚的總產量，從魚塘里捕撈了三次，得到如下表的數據：

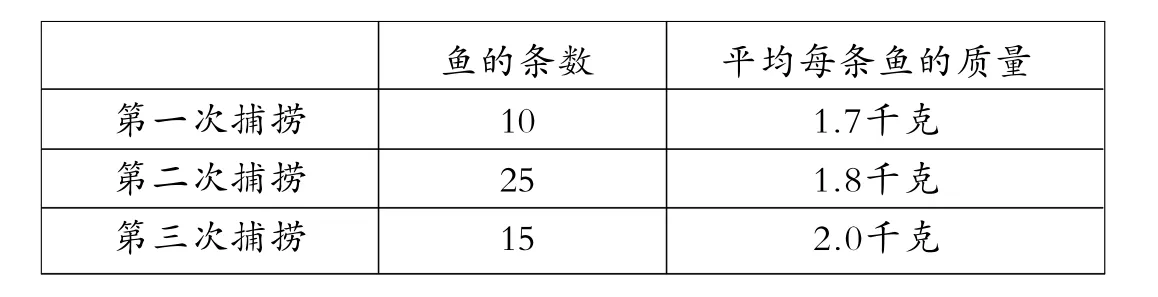
第一次捕撈第二次捕撈第三次捕撈魚的條數1 0 2 5 1 5平均每條魚的質量1.7千克1.8千克2.0千克

若老王放養這種魚的成活率是95%，請問：

（1）魚塘里這種魚平均每條重約多少千克；

（2）魚塘里這種魚的總產量是多少千克？

答：魚塘里這種魚平均每條重約1.84千克.

（2）魚的總重量為2000×95%×1.84=3496千克．

答：魚塘里這種魚的總產量是3496千克．

類型5 用樣本的平均數估算總體的平均數

例5某市對初中畢業生進行了一項技能測試，有4萬名考生的得分都是不小于70的兩位數，從中隨機抽取3000個數據，統計如下表：

數據x個數平均數7 0≤x≤7 9 8 0 0 7 8 8 0≤x≤8 9 1 3 0 0 8 5 9 0≤x≤9 9 9 0 0 9 2

請根據表格中的信息，估計這4萬個數據的平均數約為（ ）.

A．92 B．85 C．83 D．78

∴這4萬個數據的平均數約為85.

選B．

類型6 用樣本的方差估算總體的方差

例6某校九年級學生開展踢毽子比賽活動，每班派5名同學參加，按團體總分多少排列名次，在規定時間內每人踢100個以上（含100）為優秀，下表是成績最好的甲班和乙班5名學生的比賽數據（單位：個）．

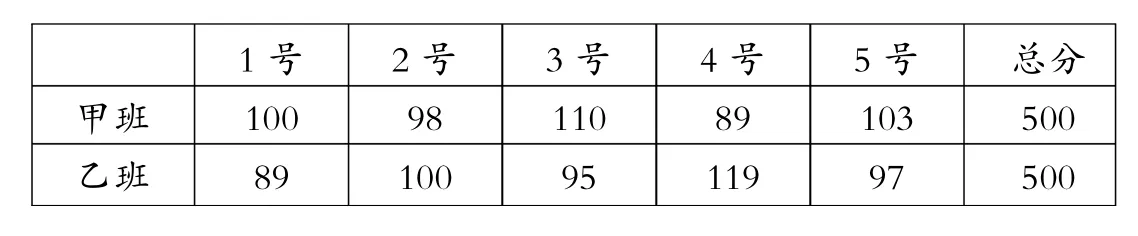
甲班乙班1號1 0 0 8 9 2號9 8 1 0 0 3號1 1 0 9 5 4號8 9 1 1 9 5號1 0 3 9 7總分5 0 0 5 0 0

統計發現兩班總分相等.此時有同學建議，可以通過考查數據中的其他信息作為參考.請你解答下列問題：

（1）計算兩班的優秀率；

（2）求兩班比賽數據的中位數；

（3）兩班比賽數據的方差哪一個小？

（2）甲班5名學生比賽成績的中位數為100（個）；

乙班5名學生成績的中位數為97（個）.

（[100-100）2+（98-100）2+（110-100）2+（89-100）2+（103-100）2]=46.8，

（89-100）2+（100-100）2+（95-100）2+（119-100）2+（97-100）2]=103.2.

答：甲班的方差比乙班的方差小.