GNSS/SINS松組合系統的可觀測性分析
肖佳敏,朱 鋒,張小紅
(武漢大學 測繪學院,武漢 430079)
0 引言
全球衛星導航系統(global navigation satellite system,GNSS)與捷聯式慣性導航系統(strapdown inertial navigation system,SINS)功能互補,二者組合之后具有導航精度高、可靠性好等特點,廣泛應用于海陸空各領域的導航。GNSS/SINS松組合系統一般采用卡爾曼濾波,對系統進行可觀測性分析有利于了解卡爾曼濾波性能,認識系統參數與狀態量估計之間的關系。松組合系統在特定情況下并非所有狀態量都是可觀測的,對不可觀測的狀態量進行濾波難以得到準確的估計結果。根據可觀測性分析結果,載體進行一定機動可以使得某些誤差狀態由不可觀測變為可觀測,為系統實現快速收斂提供參考,因此在工程實踐中有必要考慮組合導航系統的可觀測性。
由于載體運動,松組合系統為時變系統,濾波過程中狀態量的可觀測性不會一成不變,使得時變系統的可觀測性分析變得困難。文獻[1-2]提出了分段定常系統(piece-wise constant system,PWCS)可觀測性理論,將時變系統視為短時間內的定常系統,通過求系統的提取可觀測性矩陣(stripped observability matrix,SOM)簡化了對時變系統可觀測性的分析。基于PWCS可觀測性理論,國內外學者對導航系統的可觀測性進行了研究。文獻[2]分析了慣導系統飛行對準時,線運動對于提高誤差狀態可觀測性的作用。文獻[3]分析了地心地固系(e系)下,具有桿臂誤差的GPS/INS組合導航系統的可觀測性。文獻[4]分開考慮了系統的可觀測部分與不可觀測部分,對系統狀態量進行逐個分析。文獻[5]利用狀態方程解耦的思想降低了系統SOM的復雜度,并給出誤差狀態可觀測性與載體線運動、角運動之間的聯系。
e系下的松組合濾波模型中姿態誤差表示在載體系下,減少了后續可觀測性分析的工作[6]。但實際中對載體而言e系下運動方向不明,不便于對載體機動進行確切的指導以達到提高狀態量可觀測性的目的,而當地水平坐標系(n系)物理意義明確,對載體而言操作更加方便。本文選取n系作為參考系,根據實際中導航參數的數值范圍對濾波系統進行了簡化,接著利用PWCS理論求得系統的SOM,通過對狀態量進行解耦分析了桿臂誤差與位置誤差、姿態誤差與加計零偏的可觀測性,并得到了桿臂誤差、姿態誤差以及加計零偏的可觀測性與載體運動之間的聯系,最后通過仿真對結論進行了驗證。理論分析與仿真測試證明了載體運動可以使得系統狀態量由不可觀測變為可觀測,從而提高狀態量的估計速度及精度,對工程實踐有指導意義。
1 18維狀態的松組合數學模型
本文采用n系下的GNSS/SINS松組合模型作為可觀測性分析的對象,建立了18維狀態的系統狀態模型,包括位置誤差δrn、速度誤差δvn、失準角φ、加計零偏ab、陀螺零偏εb和桿臂誤差δlb。在不考慮系統噪聲的情況下,n系下松組合的系統狀態方程[7-8]為
(1)

同樣不考慮觀測噪聲的情況下,松組合觀測方程[7,9]為
(2)
式中:Z為觀測向量;Ln為桿臂值。
由于系統狀態方程式中的系數矩陣F十分復雜,不利于后續可觀測性矩陣的計算,因此,做如下模型簡化:在組合導航實際應用中,一般載體運動速度在100m/s以內,而地球半徑數量級達到1×106m,因此矩陣F的子矩陣Frr最大在1×10-4數量級,而慣導系統中位置誤差δrn在1×10-3數量級左右,二者乘積遠小于速度誤差δvn數量級1×10-4對于位置誤差微分的影響,因此,位置誤差微分方程可以簡化[4]為
(3)
同理,子矩陣Fvr、Fvv、Fφr、Fφv數量級均較小,對相應狀態量的影響可以忽略,簡化后的系統狀態方程為
(4)
2 n系下的可觀測性矩陣
組合導航系統為連續時變系統,不能直接利用可觀測性矩陣來分析。但根據PWCS可觀測性分析理論,在短時間內,可以認為系統是時不變的。由式(2)、式(4),計算系統在第j個時間間隔內的SOM[1]為
(5)
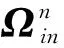
對式(5)進行行變換后得到
(6)
矩陣維數為54×18,式中矩陣4行以下為42×18的零陣。
(7)
3 可觀測性分析
根據式中非零陣元素的分布,可以發現位置誤差與桿臂誤差相互耦合,與其余4種誤差解耦。速度誤差可觀測,載體姿態誤差與加計零偏、陀螺零偏耦合。
3.1 位置誤差與桿臂誤差的可觀測性分析
根據式(7),由PWCS可觀測性理論可以得到表示位置誤差及桿臂誤差的可觀測性矩陣為
(8)
式中下標16表示位置誤差與桿臂誤差在狀態量中的位置。
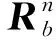
具體考慮2個時間段內的可觀測性矩陣。假設開始時載體處于靜止狀態,2個時間段內的可觀測性矩陣為
(9)
(10)
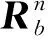
因此有結論1:位置誤差與桿臂誤差耦合在一起,載體的角運動將提高桿臂誤差的估計,而直線運動對于桿臂誤差的可觀測性沒有貢獻。載體繞某方向的角速度將使得垂直于該方向的桿臂誤差可觀測。
3.2 姿態誤差、加計零偏與陀螺零偏的可觀測性分析
根據式(7),由PWCS可觀測性理論可以得到表示姿態誤差、加計零偏及陀螺零偏的可觀測性矩陣
(11)
式(11)經行變換后可以拆分成
(12)
(13)
式中:Q34表示姿態誤差與加計零偏的可觀測性矩陣;Q35表示姿態誤差與陀螺零偏的可觀測性矩陣。
觀察矩陣Q34、Q35,可以發現這3種誤差的可觀測性與載體的直線運動、角運動均有關系。矩陣Q35中含有n系相對于慣性系的角速度,載體不可控,下面僅對矩陣Q34進行分析,考慮載體分別進行線運動及角運動。
1)載體線運動
(14)
(15)
現考慮2個時間段內的可觀測性,開始時載體處于靜止狀態下,且載體天向與導航系U向保持一致,則可觀測性矩陣為
(16)
由于載體靜止,有
(17)
式中g為重力加速度。
因此,式(16)可以展開為
(18)
式(18)第3行非零項對應az(天向加計零偏),也就是說靜止時有az可觀測。假設載體下一時間段Fb發生改變,例如載體向前加速,有fx=0,fy≠0,fz=g,因此2個時間段的可觀測性矩陣為
(19)
因此有結論2:載體在某一水平方向上進行加速運動,將提高該方向上加計零偏的可觀測性。直線運動時,姿態誤差的可觀測性與水平向加計零偏的可觀測性耦合,而與天向加計零偏的可觀測性解耦。
2)載體角運動
(20)
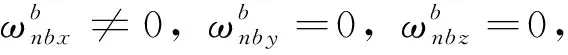
(21)

4 仿真驗證
利用仿真數據對上述3條結論進行驗證。
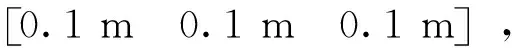
分別設計3個實驗:實驗一確定靜止狀態下可觀測的狀態量,仿真靜止800 s,濾波初始狀態量均為0。實驗二,載體先靜止100 s,接著以1 m/s2向前加速10 s,然后保持10 m/s的速度勻速向北向運動。整個過程中只有北向速度發生了變化。實驗三,載體先靜止100 s,接著以1 m/s2向前加速10 s,然后保持10 m/s的速度勻速向北向運動,100 s之后以2°/s的速度向左轉90° ,朝西運動100 s最后以2 m/s2減速至0。
根據卡爾曼濾波方差的收斂速度可以判斷狀態量的可觀測度[10],若其濾波方差未收斂,則說明該狀態量不可觀測,濾波方差收斂越快,說明狀態量可觀測度越高。仿真結果分析如下。

圖2為姿態誤差的濾波結果,圖3為加計零偏的濾波結果。實驗一中,載體靜止時右向及前向姿態誤差收斂,而天向姿態誤差可觀測性較差。由圖3(a)、圖3(b)可以看到靜止時右向及前向加計零偏濾波STD為9.8×10-4m/s2,且沒有收斂趨勢,完全不可觀測,而圖3(c)中天向加計零偏可觀測。實驗二中,100 s后載體向前加速,將提高前向(y向)加計零偏的可觀測性,圖3(e)顯示y向加計零偏STD在100 s后開始收斂,但收斂趨勢不明顯,說明可觀測性仍很差。但此時圖3(d)中x向加計零偏依舊不可觀測,說明載體的前向加速運動可以提高前向加計零偏的可觀測性。同時載體直線運動時,姿態誤差的可觀測性與水平方向上的加計零偏耦合,實驗二中100 s后前向加計零偏可觀測性的提高也將提高天向姿態誤差的可觀測性,圖2(f)顯示實驗二中100 s后天向姿態誤差STD收斂加快。驗證了結論2。
實驗三中210 s后載體天向角速度發生變化,將提高水平向加計零偏的可觀測性,圖3(g)、圖3(h)顯示水平向加計零偏在210 s后收斂至0,驗證了結論3。
5 結束語
本文研究了n系下GNSS/SINS松組合濾波狀態參數的可觀測性,包括桿臂誤差、姿態誤差以及加計零偏。通過分析3種狀態參數的可觀測性與載體角運動、線運動之間的關系,得到了以下3條結論:1)位置誤差與桿臂誤差耦合,載體的角運動將提高桿臂誤差的估計,而直線運動對于桿臂誤差的可觀測性沒有貢獻,載體繞某方向的角速度將使得垂直于該方向上的桿臂誤差可觀測;2)載體在某一水平方向上進行加速運動將提高該方向上加計零偏的可觀測性,直線運動時姿態誤差與水平方向的加計零偏耦合,而與天向加計零偏解耦;3)載體只進行角運動時,繞某方向的角運動將使得垂直于該方向上的加計零偏可觀測。最后通過仿真實驗,驗證了本文的可觀測性分析結論。工程實踐中,在組合導航初始對準階段,進行加速及轉彎,可以加快濾波狀態量的收斂速度,快速實現高精度導航定位。

