層間位移約束下高層框架-支撐結構的單步優(yōu)化法

孫飛飛， 馬志東， 賈瑞梓

(1.同濟大學 土木工程防災國家重點實驗室，上海 200092；2.同濟大學 土木工程學院，上海 200092)

為保證高層建筑結構具有必要的剛度，現(xiàn)行國家標準《高層建筑混凝土結構技術規(guī)程》[1]和《高層民用建筑鋼結構技術規(guī)程》[2]均對高層建筑層間位移角限值做出規(guī)定.合理地控制結構側移以保證結構的安全性和正常使用，也是結構設計達到經(jīng)濟、合理的重要因素[3].

為了解決層間位移約束下高層建筑結構的優(yōu)化問題，多種基于數(shù)學優(yōu)化算法的結構優(yōu)化設計方法被提出.Chan等[4-5]將準則法應用于水平側移約束下鋼和混凝土框架結構的優(yōu)化設計中，通過一系列簡化假定，利用虛功原理推導準則法迭代公式，并將該方法用于香港某高層建筑結構的初步設計中，取得良好效果.李志強[6]根據(jù)最優(yōu)化準則Kuhn-Tucker條件推導出型鋼混凝土結構框架柱混凝土截面尺寸的迭代公式，將其與層次分析遺傳算法相結合，建立了層次分析優(yōu)化準則遺傳算法(OC-GA).白代春[7]采用離散變量分步優(yōu)化的規(guī)劃法對鋼筋混凝土框架進行優(yōu)化，并設計了一個平面框架結構優(yōu)化設計程序，實現(xiàn)結構自動分析及優(yōu)化.此外，SAP2000有限元分析軟件具有鋼結構優(yōu)化設計的輔助功能.實際工程體量大、優(yōu)化問題復雜，而工程師往往需要手動對結構進行調(diào)整，上述各方法尚不能提供一個快捷的調(diào)整建議，實用的成熟度還不夠，因此本文旨在提出一種單步、高效的優(yōu)化方法.

本文首先考察高層建筑規(guī)則結構的變形機制，根據(jù)結構變形規(guī)律將層間位移約束下的高層建筑規(guī)則結構多約束優(yōu)化問題等效轉(zhuǎn)化為單約束優(yōu)化問題.在此基礎上，提出基于結構整體轉(zhuǎn)動比虛應變能的單步優(yōu)化法，擬通過簡單的優(yōu)化過程為工程師提供高效實用的設計建議.

1 高層建筑規(guī)則結構的層間位移機制

為了簡化高層建筑規(guī)則結構層間位移約束下的結構優(yōu)化方法，首先需要理解層間位移約束下高層建筑規(guī)則結構的變形機制.

1.1 算例的結構信息

算例為圖1中60層7跨的高層框架-支撐結構.結構劃分為240個構件組，每組構件的截面相同，分組方式為：每兩層相對稱的柱為一組，共120組；每一層的支撐為一組，共60組；每一層的梁為一組，共60組.不考慮豎向荷載作用，風荷載簡化為分布荷載施加于樓層.位移約束條件為層間位移角，限值為1/400.

圖1 框架支撐結構算例Fig.1 Example of braced-frame structure

1.2 各樓層對目標樓層層間位移角的貢獻規(guī)律

取整十層樓層為例，由虛功原理計算各樓層對層間位移角的貢獻，如下所示：

(1)

式中：θt為目標層的層間位移角(t=10,20,…,60)；θt,j為j層對t層層間位移角的貢獻(j=1,2,…,60).

將各樓層對整十層層間位移角的貢獻分離開，如圖2所示.

由圖2可知，除接近頂部的樓層，各樓層對本層層間位移角的貢獻最為突出，對上下相鄰約10層范圍內(nèi)的貢獻也較大并向外遞減.這是由樓層的局部變形協(xié)調(diào)和傳力關系所致，這種局部效應類似于彈性力學中的圣維南原理，本文稱這段區(qū)域為圣維南區(qū)域.10層以外，上部貢獻值較小且平緩，下部貢獻曲線基本一致，理解為由下部樓層剛體轉(zhuǎn)動所致.因此，60層的層間位移角分離曲線中，除上部10層的貢獻由受力和變形協(xié)調(diào)決定外，下部50層的貢獻值即為樓層整體轉(zhuǎn)動量.

圖2 第j層對第t層層間位移角的貢獻Fig.2 Contribution of jth floor to the inter- story drift of tth floor

1.3 某一樓層對各層層間位移角的貢獻規(guī)律

相似地，可以計算出某一樓層對結構各層層間位移角的貢獻.圖3為整十層對結構各層層間位移角貢獻曲線.由圖3可知，各樓層對本層層間位移角的貢獻最大，對上下相鄰約10層范圍內(nèi)樓層的層間位移角貢獻也較大且向外遞減.這同樣是由于局部變形協(xié)調(diào)和傳力關系所致.上下10層范圍以外，該樓層對下部的貢獻非常小，對上部的貢獻趨于一致.

圖3 整十層對層間位移角的貢獻Fig.3 Contribution of each 10th floor to inter-story drift

1.4 整體轉(zhuǎn)動對層間位移角的貢獻規(guī)律

將層間位移角θt分離成由目標樓層剛體轉(zhuǎn)動引起的層間位移角θ1、本層受力層間位移角θ2、由剪力滯后引起的附加層間位移角θ33個部分之和，如下所示：

θt=θ1+θ2+θ3

(2)

圖4為結構的層間位移角分離曲線.由圖4可見：在結構底部本層受力和局部變形協(xié)調(diào)的貢獻很大，整體轉(zhuǎn)動的貢獻不明顯；在結構中上部，本層受力和局部變形協(xié)調(diào)的貢獻較小并向上逐漸減小，結構的整體轉(zhuǎn)動在層間位移角中占主要部分.

圖4 層間位移角分離曲線Fig.4 Separation curve of inter-story drift

1.5 不同構件對結構頂部轉(zhuǎn)動的貢獻規(guī)律

將構件對樓層整體轉(zhuǎn)動的貢獻分離，可以明確各類構件的效率，確定層間位移約束下結構優(yōu)化的主動變量.各類構件對樓層整體轉(zhuǎn)動的貢獻可以通過在結構頂部加單位彎矩虛荷載計算得到.分別計算柱、梁、支撐對樓層整體轉(zhuǎn)動的貢獻，如圖5所示.

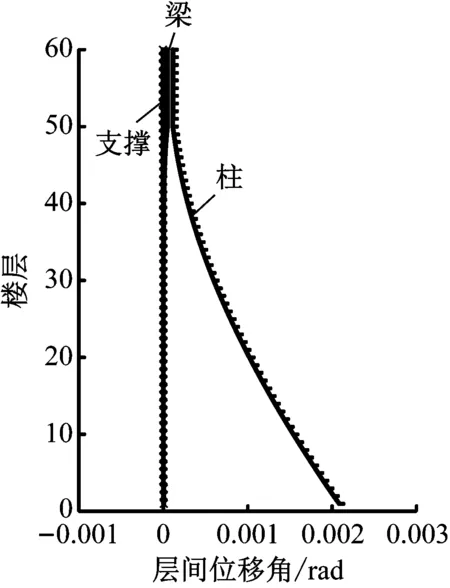
圖5 層間位移角按構件分離曲線Fig.5 Separation curve of inter-story drift by elements

由圖5可見，樓層整體轉(zhuǎn)動以柱的貢獻為主，梁和支撐的貢獻非常小.

1.6 高層建筑規(guī)則結構的變形機制

綜上分析，在高層建筑規(guī)則結構下部，本層的受力位移對層間位移角的貢獻最為突出.最大層間位移角往往出現(xiàn)在結構的中上部，在這些部位，層間位移角以結構的整體轉(zhuǎn)動為主.

2 單步優(yōu)化法的建立

基于第1.6節(jié)結構層間位移機制，將層間位移約束下的高層建筑規(guī)則結構優(yōu)化的多約束問題轉(zhuǎn)化為單約束問題，在此基礎上利用虛功準則法，建立結構單步優(yōu)化的基本方法.

2.1 層間位移約束下結構優(yōu)化問題

典型的層間位移約束下高層建筑規(guī)則結構優(yōu)化問題包括優(yōu)化目標和約束條件下的數(shù)學優(yōu)化模型，如下所示：

(3)

2.2 基本假定

假定1忽略構件的剪切變形對位移的貢獻量.由虛功原理可知，結構位移為各構件對位移的貢獻量之和.構件對位移的貢獻主要由彎曲和軸向分量組成，計算中忽略構件的剪切貢獻分量，如下所示：

(4)

(5)

式中：δi為構件i對位移的貢獻；fi、mi分別為構件i在虛荷載下的軸力、彎矩；Fi、Mi分別為構件i在實際荷載下的軸力、彎矩；Ei為構件i的材料彈性模量；Ii為構件i的慣性矩.

假定2內(nèi)力暫時不變.由式(5)可知，構件的位移貢獻量與構件面積、慣性矩成反比.假設構件截面變化前后內(nèi)力不變，則構件截面改變后，新的位移貢獻量與構件面積、慣性矩的變化率成比例，如下所示：

(6)

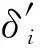
2.3 虛功準則法

(7)

(8)

優(yōu)化問題可以轉(zhuǎn)化為與設計變量之間的直接關系，如下所示：

(9)

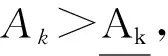
(10)

根據(jù)式(10)，對于主動變量，可得

(11)

式中：分子表示構件k對層間位移角θ的貢獻量，也是構件k的虛應變能；分母中LkAk表示構件k的體積；γk表示構件k的比虛應變能.因此，式(11)可以理解為最輕結構中，相應于主動變量的構件中單位體積的虛功即構件的比虛應變能γk相等.

2.4 單步優(yōu)化法的提出

基于層間位移約束的單步優(yōu)化法的提出是為了給工程師提供快速實用的優(yōu)化建議，但假如簡單地以結構最大層間位移角作為優(yōu)化的主要約束進行單步優(yōu)化，那么僅本層及相鄰層構件的尺寸將被加強，得到結構局部過剛的不合理結果.因此，單步優(yōu)化法的有效約束與比虛應變能的選擇將對優(yōu)化結果的合理性產(chǎn)生重要影響.

2.4.1約束條件的轉(zhuǎn)換

為了避免結構局部過剛的問題，本節(jié)提出層間位移約束下結構優(yōu)化的設計思想：如果結構整體轉(zhuǎn)動的比虛應變能均勻并且最大層間位移角滿足約束條件，相應結構對于層間位移約束問題是一個較優(yōu)解.由第1節(jié)可知，將層間位移約束下高層建筑規(guī)則結構的優(yōu)化轉(zhuǎn)化為針對結構整體轉(zhuǎn)動的優(yōu)化，即通過結構頂部整體轉(zhuǎn)動的減小來滿足結構所需的位移角減小量，從而排除局部虛功突出的影響，保證優(yōu)化結果的合理性.

2.4.2單步優(yōu)化問題

基于以上分析，優(yōu)化問題即可轉(zhuǎn)化為可執(zhí)行的形式，如下所示：

(12)

式中：θrtop為結構頂部的整體轉(zhuǎn)動量; [θrtop]為結構頂部的整體轉(zhuǎn)動量限值.

在將層間位移約束下高層建筑規(guī)則結構的優(yōu)化約束條件進行轉(zhuǎn)換之后，就需要解決[θrtop]的取值問題，以確定結構所需的位移角減小量.

為此，考察結構頂部整體轉(zhuǎn)動所需的減小量θd，其值可由結構最大層間位移角所需的位移角減小量換算而來.具體來說，如圖6所示，假設結構的最大層間位移角θmax出現(xiàn)在第n層，第n層所需的位移角減小量為(θmax-[θ])，根據(jù)下式換算出結構頂部整體轉(zhuǎn)動所需的位移角減小量：

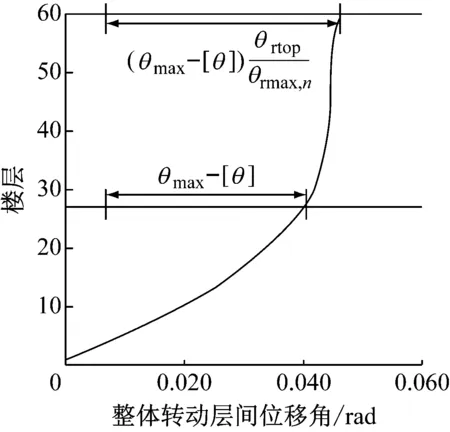
圖6 結構整體轉(zhuǎn)動曲線Fig.6 Rigid body rotation curve of the structure

(13)

式中：θrmax,n為最大層間位移角樓層處結構整體轉(zhuǎn)動量.θd確定，[θrtop]也就相應確定，如下所示：

[θrtop]=θrtop-θd

(14)

由于僅考慮結構的整體轉(zhuǎn)動減小量，故θd也是結構頂部層間位移角的減少量，可得

[θrtop]=θtop-θd

(15)

式中：θtop為初始結構頂層層間位移角.

2.4.3單步優(yōu)化過程

當優(yōu)化問題由式(9)轉(zhuǎn)化為式(12)之后，同理通過引入庫-塔克法則，優(yōu)化準則即轉(zhuǎn)換為結構整體轉(zhuǎn)動比虛應變能均勻.通過構件初始比虛應變能γi與目標比虛應變能γg關系，確定與主動變量對應的構件修正系數(shù)βi，如下所示：

( 16 )

βi一旦確定，初始結構的構件尺寸需要被加強的程度也就確定，以此實現(xiàn)單步優(yōu)化，使結構以較高的效率滿足層間位移約束條件.具體實現(xiàn)過程如下所示：

(1)確定初始結構，構件尺寸取滿足強度要求的最小截面.

(2)在結構頂部加單位彎矩虛荷載.

(3)提取初始結構的層間位移角曲線和整體轉(zhuǎn)動曲線，計算構件比虛應變能γi、結構平均比虛應變能γave.

(4)計算結構頂部轉(zhuǎn)角的目標位移角減小量θd和結構放大系數(shù)α(α的推導過程見第3.2節(jié))，確定結構的目標比虛應變能γg.

(6)根據(jù)構件修正后面積，在構件庫中選擇新截面.

(7)重新運行結構分析，檢查強度和位移約束.

3 單步優(yōu)化法的關鍵算法

3.1 構件修正系數(shù)βi的計算方法

構件修正系數(shù)βi將結構調(diào)整為比虛應變能均勻的目標結構，本節(jié)解決利用構件比虛應變能γi和目標比虛應變能γg確定構件修正系數(shù)βi的問題，并推導βi的計算公式.

由第2.2節(jié)提出的基本假定2，構件i修正后的位移貢獻如下所示：

(17)

對于型鋼構件，截面慣性矩I與面積A的關系由精確計算公式表示過于復雜.結構設計中同一類構件截面相似，可以采用線性回歸的方法確定I與A的簡單近似關系，以便簡化計算.美國鋼結構規(guī)范(AISC)提供的型鋼截面中，W14系列(W14×22～W14×730)、W24系列(W24×55～W24×492)型鋼的慣性矩I與面積A的關系如圖7a所示，可見I與A分別成近似線性關系.圖7中，1 ft=0.305 8 m.用方程I=ηA進行擬合，W14系列擬合方程為

I=0.390 9A

(18)

W24系列擬合方程為

I=0.845 6A

(19)

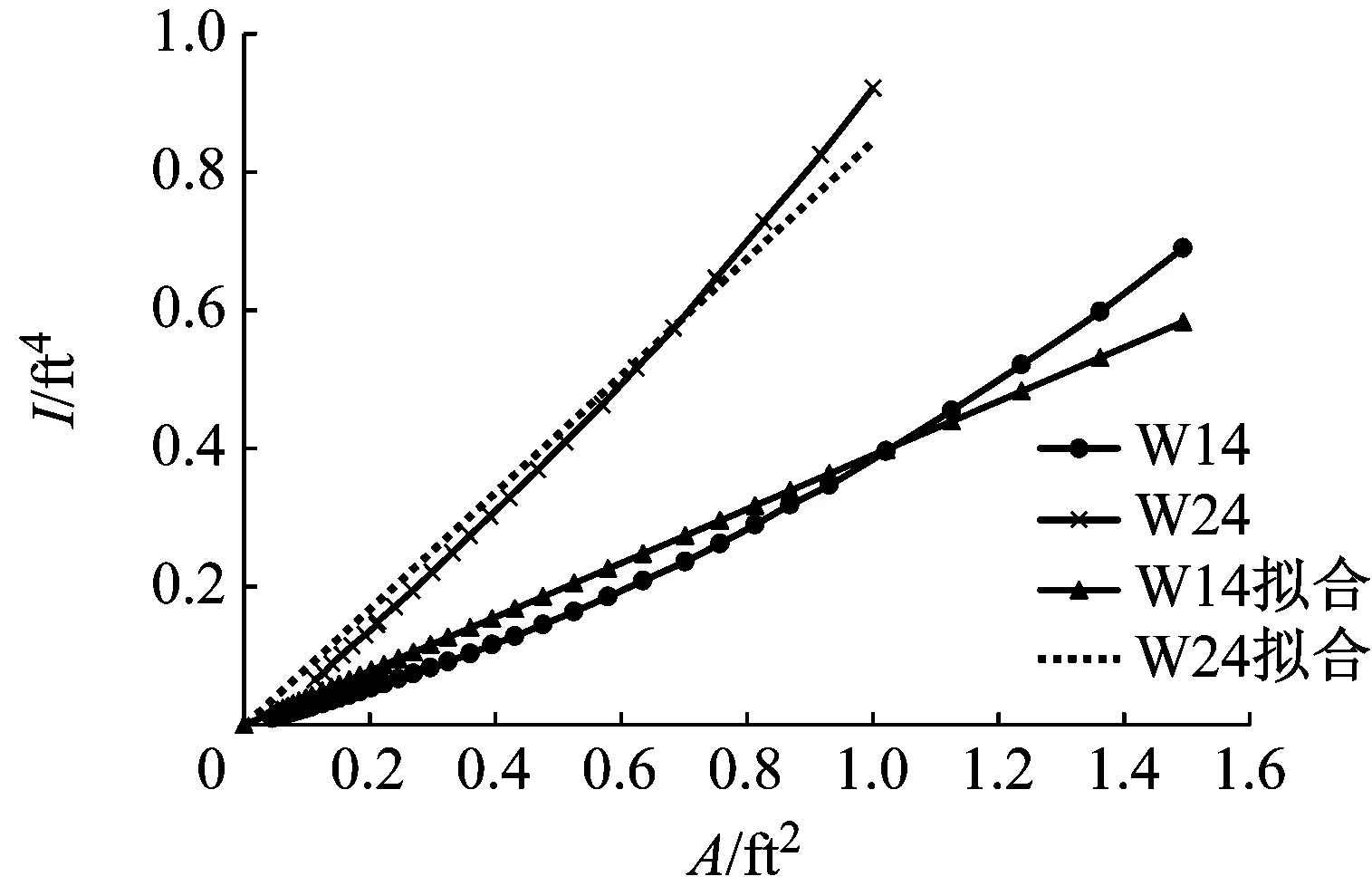
a AISC型鋼截面

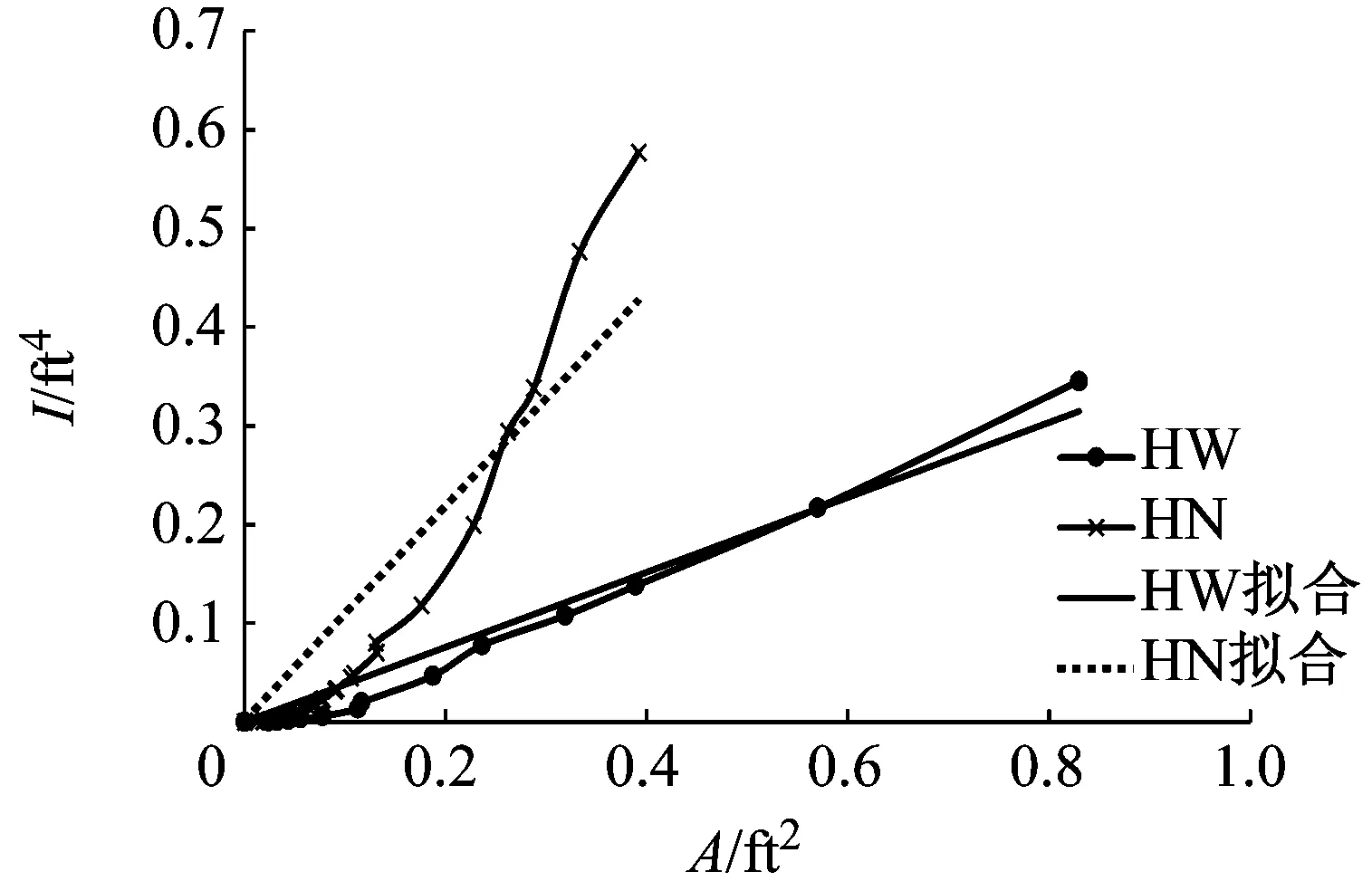
b GB型鋼截面圖7 AISC型鋼與GB型鋼截面I與A線性擬合Fig.7 Linear fitting of inertia and area of steel section in AISC and Chinese code

類似地，我國GB/T 11263—1998提供的型鋼中，HW系列(HW100×100～HW400×400)型鋼的慣性矩I與面積A的關系和擬合直線如圖7b所示.HW系列擬合方程為

I=1.094 0A

(20)

HN系列擬合方程為

I=0.379 4A

(21)

基于上述I與A的線性化回歸，有

(22)

(23)

修正后構件的比虛應變能

(24)

(25)

對于I與A成線性關系的構件庫來說，無論構件位移貢獻以軸向分量為主還是彎曲分量為主，修正系數(shù)βi的表達式是統(tǒng)一的.實際上，除了規(guī)格確定的型鋼構件外，對其他自行設計的截面形式，選取構件庫時，還可以按照I與A成線性關系的目標確定截面參數(shù)，或者對于一組構件，通過回歸的方法建立I與A的其他關系，達到減少優(yōu)化變量、簡化計算的目的.

3.2 結構放大系數(shù)α的計算方法

結構優(yōu)化中，相應于主動變量的構件根據(jù)整體轉(zhuǎn)動比虛應變能均勻的原則被修正，使得結構的層間位移角滿足約束限值.主動變量為初始比虛應變能γi較大、對位移起控制作用的構件，通過加強這些構件以補償結構剛度的不足.

結構頂層初始層間位移角θtop表達式為

∑γiAiLi+∑γAL=θtop

(26)

相應于主動變量構件的目標比虛應變能為γi，修正后的截面面積為βiAi，按照內(nèi)力暫時不變假定，設計后結構位移角表達式為

(27)

式(26)減去式(27)，得

(28)

由式(28)可知，α為相應于主動變量構件的比虛應變能、體積和結構所需的位移角減小量θd的函數(shù).通過α控制結構的放大程度，加強主動變量來補償結構剛度不足.

4 算例分析

4.1 算例

采用單步優(yōu)化法對圖1中結構進行層間位移約束下的優(yōu)化.樓層整體轉(zhuǎn)動以柱的貢獻為主，確定框架柱截面尺寸作為優(yōu)化設計的主動變量.滿足強度和穩(wěn)定性要求的初始結構最大層間位移角為0.013 1，出現(xiàn)在第25層，故需對該結構進行優(yōu)化使其滿足層間位移約束.

4.2 單步優(yōu)化法的優(yōu)化結果

單步優(yōu)化法的截面結果如表1所示，位移角結果如圖8所示，最大層間位移角為0.003 81，出現(xiàn)在第26層，而25層的層間位移角為0.003 80.由優(yōu)化結果可見，最大層間位移角位置發(fā)生變化，與初始最大層間位移角的位置靠近，層間位移角最大的區(qū)域均接近位移角限值.樓層整體轉(zhuǎn)動曲線相比初始結構更加趨于平緩，這是“結構整體轉(zhuǎn)動的比虛應變能均勻”的結果.

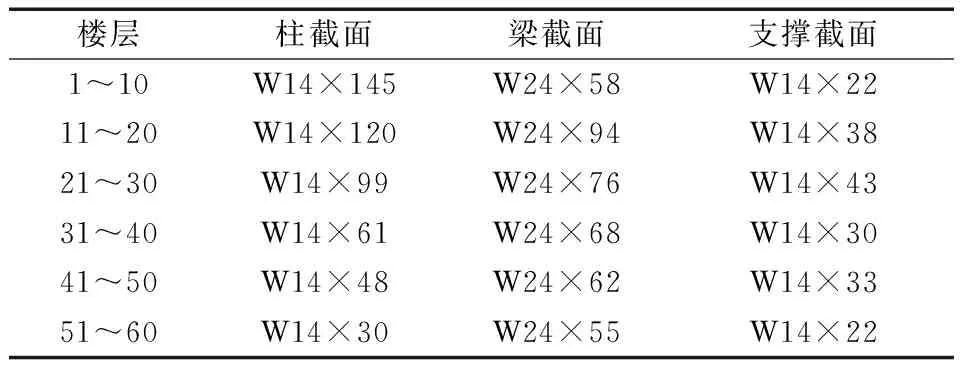
表1 構件截面優(yōu)化結果Tab.1 Optimized cross-section of the elements

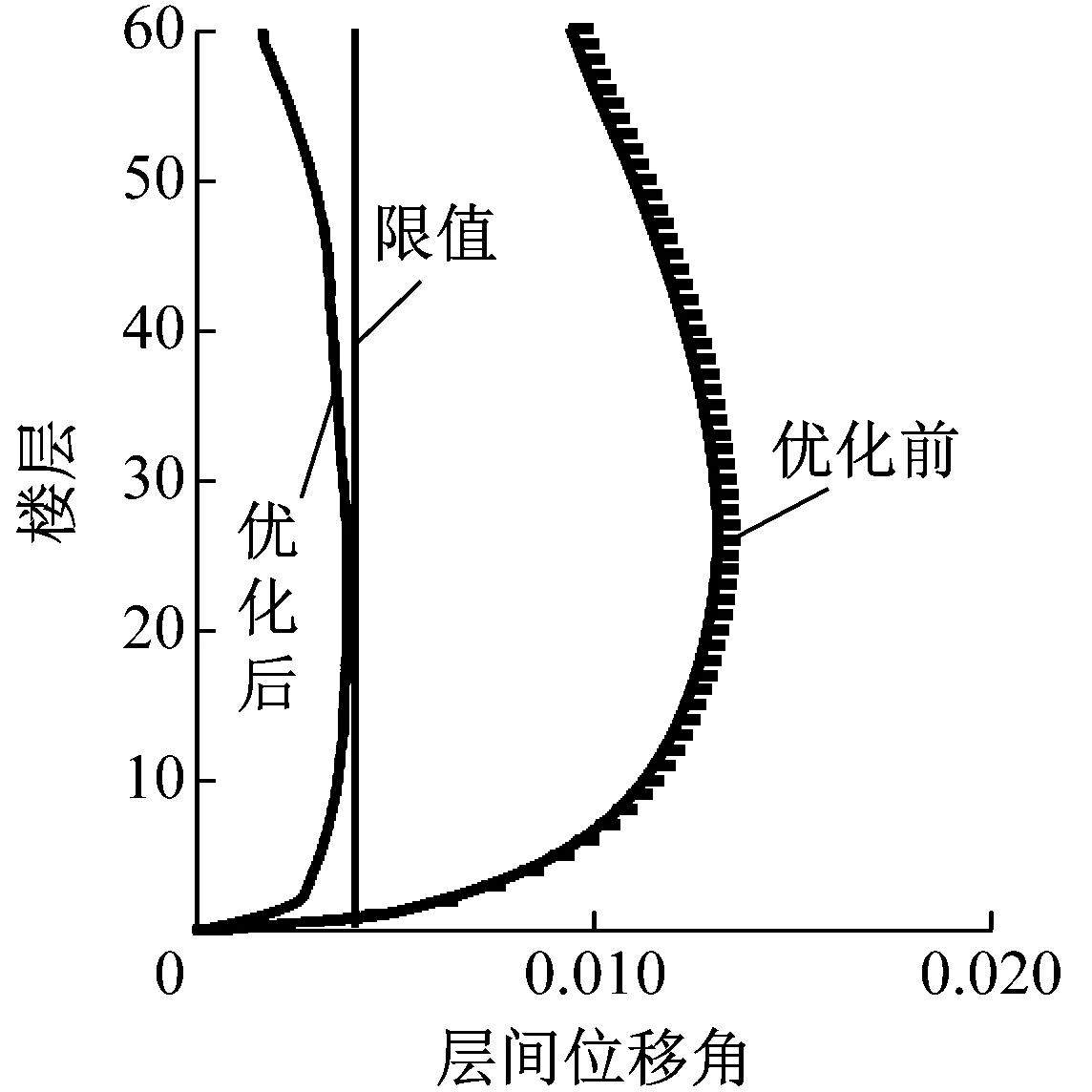
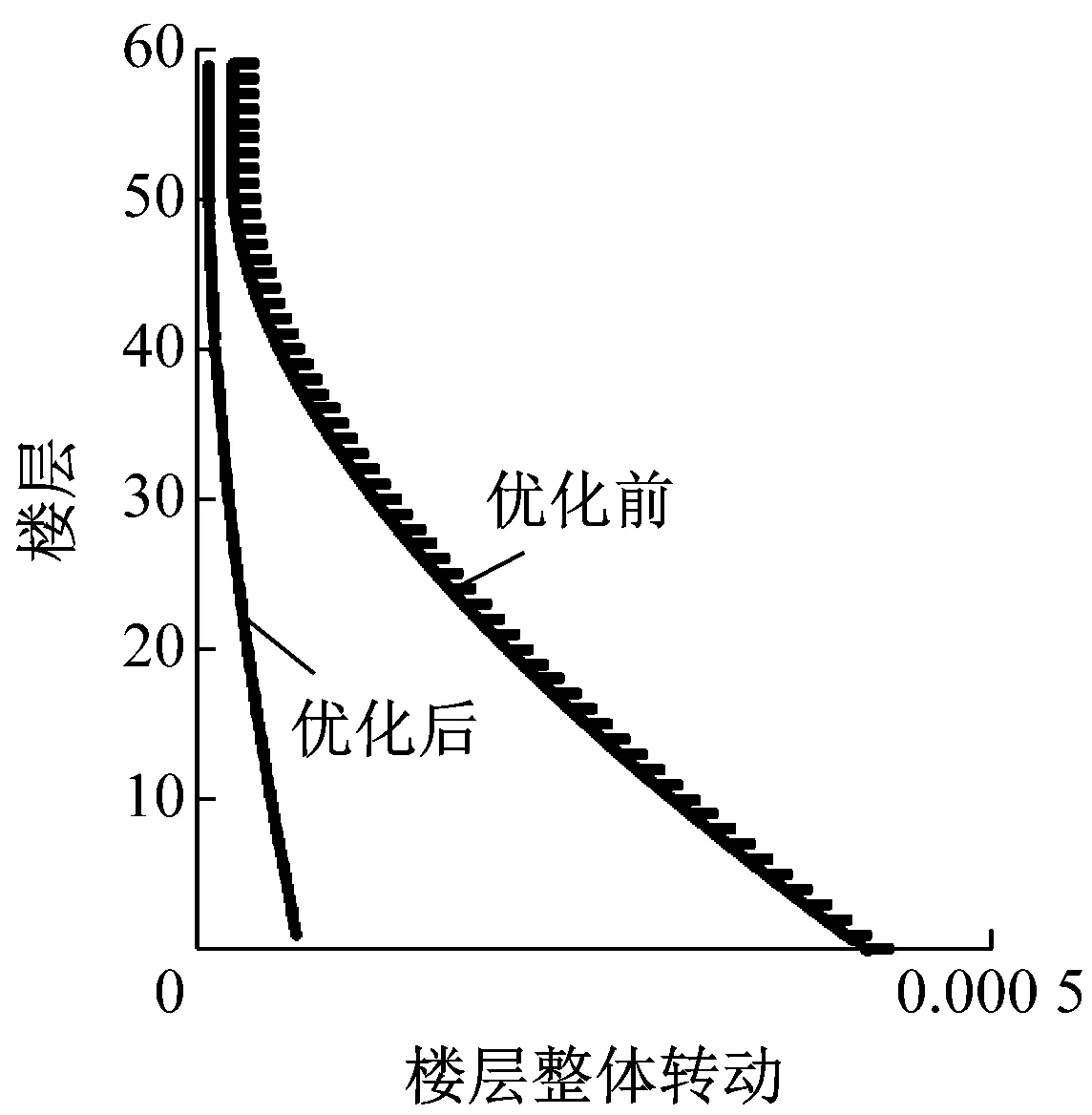
圖8 單步優(yōu)化法優(yōu)化結果Fig.8 Results of single-step optimization method

應用實例表明,所提出的方法達到了預定的設計目標，穩(wěn)定承載力也滿足要求，結果合理，方法可行.

4.3 不同優(yōu)化方法優(yōu)化結果對比

SAP2000作為強大的結構設計軟件，為用戶提供了以位移或者周期為目標的鋼結構自動優(yōu)化功能.對于位移優(yōu)化，SAP2000軟件預測哪個構件需要增加尺寸，以控制基于構件內(nèi)單位體積能量的位移.單位體積能量更多的構件比能量更少的構件需要增加更大的比例尺寸.只要所考慮的強度允許，有些單位體積能量小的構件是可以減小尺寸的[9].在SAP2000軟件“設計”菜單中，通過對“鋼框架設計”設置風荷載工況下的側向位移目標.基于上述位移目標，SAP2000軟件可以提供對結構的構件截面自動校核與設計.

本文將單步優(yōu)化法的優(yōu)化結果與SAP2000軟件的優(yōu)化結果進行對比，結構優(yōu)化結果的總質(zhì)量分布如表2所示，結構質(zhì)量分布如圖9所示.結果表明：結構總質(zhì)量相近，質(zhì)量分布趨勢總體一致，證明了單步優(yōu)化法的有效性；相比于SAP2000軟件的優(yōu)化結果，采用單步優(yōu)化法用鋼量降低了約10%.

a 單步優(yōu)化法優(yōu)化結果b SAP2000軟件優(yōu)化結果

圖9 優(yōu)化結果質(zhì)量分布Fig.9 Mass distribution of optimized structures表2 優(yōu)化設計結果質(zhì)量對比Tab.2 Mass comparison of two optimization methods

單步優(yōu)化法與SAP2000軟件優(yōu)化后的樓層側移及層間位移角分布對比如圖10所示.雖然2種方法的結果都使層間位移角達到限值要求，2種方法優(yōu)化過程耗時也沒有顯著的區(qū)別，但是SAP2000軟件優(yōu)化結果對層間位移角限制得更嚴格，這對結構效率以及經(jīng)濟性來說是不利的.單步優(yōu)化法優(yōu)化后，結構的最大層間位移角更接近層間位移角限值.

5 結論

(1)通過將高層建筑規(guī)則結構層間位移的多約束問題轉(zhuǎn)化為單約束問題實現(xiàn)結構的單步優(yōu)化.

a 樓層位移對比

b 層間位移角對比圖10 單步優(yōu)化法與SAP2000軟件優(yōu)化結果對比

Fig.10Comparisonofoptimizationresultsbetweensingle-stepoptimizationmethodandSAP2000software

(2)在高層建筑規(guī)則結構中，最大層間位移角往往出現(xiàn)在結構的中上部，而在這些部位，層間位移以結構的整體轉(zhuǎn)動為主，這是實現(xiàn)結構單步優(yōu)化的基礎.

(3)基于虛功準則法的單步優(yōu)化法根據(jù)結構整體轉(zhuǎn)動比虛應變能調(diào)整構件截面尺寸，使結構整體轉(zhuǎn)動比虛應變能趨于均勻分布并滿足層間位移約束，算法物理意義明確，易于掌握.

(4)將單步優(yōu)化法的優(yōu)化結果與SAP2000軟件的優(yōu)化結果進行對比，在都能達到位移限值優(yōu)化目標下，基于虛功的單步優(yōu)化法用鋼量降低約10%.