城市高架軌道多層隔振系統影響參數匹配

劉 艷， 羅雁云

(1.上海材料研究所，上海 200437；2.同濟大學 鐵道與城市軌道交通研究院，上海 201804)

近年來，隨著我國城市規模不斷擴大以及人口數量和出行需求的增加，城市軌道交通持續快速發展.高架軌道結構因其用地少、施工周期短等突出優勢在城市軌道交通建設中應用廣泛.調查結果表明，世界范圍內有491條主要城市軌道交通線路，總長7 016 km，采用高架軌道形式的線路總長4 248 km，約占60.5%[1].然而，很多高架軌道結構緊鄰城市聲振敏感區域，由輪軌沖擊作用產生并傳遞至橋梁結構的振動，以及因振動誘發的低頻輻射噪聲引起居民強烈的煩惱反應，使得投訴事件屢見不鮮[2].

城市高架軌道振動問題已引起國內外學者的普遍關注，車-橋耦合動力學分析[3]、振動傳播衰減路徑分析[4]、沿線環境振動預測和評估分析[5-6]等距今已有數十年的研究歷史.此外，軌道交通振動控制技術也較為成熟，包括振源控制、吸振、消振和隔振技術.輪軌接觸是軌道交通的振動源，凡是能減小輪軌動力作用的措施均能起到減振作用[7]，如調節列車運行速度、采用重型鋼軌、減少鋼軌接頭、定期打磨鋼軌等.吸振和消振技術在高架軌道中的應用主要有鋼軌動力吸振器和橋梁動力吸振器等[8-10].從能量角度而言，該技術將受控對象的振動能量轉移到動力吸振器上以抑制動態響應，或利用附屬阻尼元件的拉伸和剪切變形消除振動能量，從而降低共振頻率附近的動態響應幅值和寬頻隨機激勵下動力響應的均方根值.城市高架軌道振動控制領域應用最廣泛的是隔振技術，減振扣件、彈性軌枕、浮置板道床、軌道橋梁支座以及在環境土體中設置的波阻塊、隔振明溝、隔振填充溝、隔振墻等都是從傳遞路徑入手，減小軌道結構振動能量向沿線建筑和土體環境進行有效傳遞[11-14].可見，城市高架軌道振動問題的理論和改善措施已具備較深入的研究基礎.然而，對于一個同時包含軌下-(枕下)-軌道板下-梁下多層彈性元件的多自由度復雜隔振系統而言，即便在幾十到幾百赫茲的局部特征頻率范圍內高架軌道交通自上而下各層子系統之間仍然具有較強的耦合作用.在城市高架軌道振動控制方面，對于彈性扣件-軌道板支承-橋梁支座所組成的多層隔振系統內部耦合機理、參數影響規律及參數匹配原則的研究目前尚不多見[15].

本文將詳細討論列車運行條件下軌下、軌道板下、梁下各層隔振元件之間的協同和制約關系，以及各參數對車體、軌道結構及橋梁結構振動響應特性的影響規律，并進行參數匹配研究.

1 現場試驗

1.1 試驗概況

選擇我國某城市軌道交通1號線2個高架線路斷面進行現場振動測試，2個測試斷面均為直線區段，橋梁形式均為30 m雙線簡支箱梁，梁高1.8 m，墩高11 m，箱梁橫斷面如圖1所示.兩斷面均采用WJ-2A型扣件系統，靜態剛度為20 kN·mm-1.對于普通整體道床(斷面I)，采用500g、100g、50g壓電式加速度傳感器測試鋼軌Z1、軌道板Z2以及橋梁的頂板Z3、底板Z4、腹板Z5和翼板Z6在車輛運行條件下的垂向振動加速度，斷面測點在橋梁跨中位置，測點布置示意圖如圖2所示.其中，字母Z表示振動測點，數字為測點編號.對于道床墊式浮置板結構(斷面Ⅱ)，由于測試條件限制，僅布置了鋼軌Z1、軌道板Z2、橋梁頂板Z3 3個垂向加速度振動測點.道床墊式浮置板結構又稱連續式浮置板，本文所涉及試驗段軌道板支承剛度約為50 kN·(mm·m2)-1.試驗車輛為實際運營地鐵B型車，6節編組，轉向架中心距12.6 m，轉向架軸距2.3 m，最高速度80 km·h-1，測試選取左側下行線.

圖1 箱梁橫斷面(單位：cm)Fig.1 Cross section of the box beam (unit: cm)

1.2 試驗結果

試驗獲取的2個斷面各測點全頻段振動加速度級La=20lg(a/a0)，如表1所示.其中，振動加速度級La的單位為dB，a和a0分別為實測加速度和基準加速度(1×10-6m·s-2).由表1中普通整體道床(斷面I)的測試數據可知，鋼軌振動加速度級最大，自鋼軌向道床結構振動衰減32 dB，進而向橋梁頂板處衰減約5 dB.橋梁的頂板、腹板和翼板的振動較接近，由于底板為彈性支承的薄壁板狀結構，其振動呈現一定程度的放大.對比表1中道床墊式浮置板結構(斷面Ⅱ)與普通整體道床，2種道床形式的鋼軌振動加速度級雖基本一致，但道床墊式浮置板結構由鋼軌向道床的振動衰減相對較小，約為22 dB，而進一步向橋梁結構的振動衰減高達25 dB.道床墊式浮置板結構對橋梁及下部基礎結構具有更顯著的隔振效果.然而，從能量角度而言，道床墊式浮置板結構有效隔離的振動能量被重新分配并聚集在上部軌道結構中，引發軌道板振動放大.圖3、4為測試結果的全頻段特征.由于篇幅所限且方便比較，圖3、4中僅列出了斷面I和Ⅱ鋼軌、軌道板、橋梁頂板的加速度頻譜.由圖3可知:截面I鋼軌振動的卓越頻率為中高頻段，430～730 Hz；軌道板振動的卓越頻率為40～75、400～450 Hz；橋梁頂板振動的卓越頻率為35～65 Hz.由圖4可知，相對截面I而言，截面Ⅱ鋼軌和軌道板的優勢振動頻率范圍未發生顯著變化，但軌道板的響應幅值在全頻段均遠大于普通整體道床.此外，截面Ⅱ橋梁頂板的振動卓越頻率雖仍為35～65 Hz，但振幅明顯降低，并且道床墊式浮置板結構有效隔離了大于100 Hz的振動能量.頻譜圖反映的2個截面振動信息與表1所示的振動特性總體一致.

圖2 測點布置示意圖Fig.2 General layout of vibration measuring point

圖3 斷面I振動測點頻譜Fig.3 Spectrum of measurement points in section I

圖4 斷面Ⅱ振動測點頻譜圖Fig.4 Spectrum of measurement points in section Ⅱ表1 各測點振動加速度級Tab.1 Measured vibration acceleration leveldB

2 建模分析

2.1 車體模型

不考慮組合列車的影響，僅考慮一節列車的動力學性能以及車輛點頭、搖頭、浮沉、側滾、橫移5個方向的自由度.將車體定義為剛體，并在幾何中心施加質量和轉動慣量，車體通過二系懸掛支撐在轉向架上，二系懸掛用Cartesian單元表征，車輛參數如表2所示.轉向架構架同樣定義為剛體，考慮點頭、浮沉和側滾3個自由度，轉向架構架與輪對之間的一系懸掛定義為線性彈簧/阻尼單元.

2.2 高架軌道結構模型

以斷面I為例說明建模過程.基于工程模擬有限元仿真平臺Abaqus，建立車-軌-橋多層隔振系統耦合模型.采用60軌，軌道板單塊板長6.0 m，寬2.7 m，一跨橋等間距裝配5塊軌道板.如圖5所示，相鄰兩跨軌道橋用于排除車輪行走過程中可能引起的邊界效應[16].圖5中，虛線框位置為車輛運行起點，即第1根車軸駛入中間跨橋面板，車輛運行終點為最后1根車軸駛出中間跨橋面板.振動加速度輸出值取圖5中虛線框所示的跨中截面響應值.為有效獲取軌道板和橋梁結構的振動傳遞特性，軌道板、梁體和墩體均采用八節點非協調實體單元C3D8I.為方便下文詳細討論高架軌道多層隔振系統彈性參數的影響規律及匹配原則，扣件、軌道板支承、橋梁支座均定義為三向線性連接屬性.由于橋墩整體質量較大，并且橋墩底部通過樁基礎埋在土體中，在列車荷載作用下，橋墩振動相對較小，因此本文在建模時不考慮橋墩的接地彈簧屬性.

表2 車輛參數Tab.2 Vehicle parameters

圖5 高架軌道結構有限元模型Fig.5 Finite element model of integrated viaduct rail

2.3 輪軌接觸模型

所建立有限元模型中，選用面-面接觸來定義輪軌接觸屬性.將車輪踏面定義為主面，鋼軌軌頭上表面定義為從面.為提高模型的收斂性，設立2個加載步建立接觸.第1步，通過小荷載平穩建立輪軌接觸關系；第2步，將車輛、轉向架的重力施加給鋼軌.

輪軌接觸屬性的定義包括輪軌間法向作用和切向作用.赫茲非線性接觸模型為

(1)

式中：P(t)為輪軌間法向作用力；G為輪軌接觸常數，與車輪踏面外形有關，對于磨耗型踏面車輪，G=3.86×R-0.115×10-8，其中R為輪軌接觸點處車輪滾動半徑；δZ(t)為輪軌接觸點處的彈性壓縮量.根據式(1)求解出輪軌間不同彈性壓縮量所對應的法向作用力.利用Abaqus“軟”接觸中的表格形式，定義輪軌間法向作用關系.表格中輸入的數據是輪軌間法向作用力與彈性壓縮量曲線中的離散點，如果模型中某一時刻的變形量介于兩點之間，則輪軌間的法向力為兩點間的線性插值.

輪軌間的切向作用力

F=μP(t)

(2)

μ取0.25.

2.4 輸入激勵

考慮車體質量及車輛經過時鋼軌幾何不平順(高低)的共同作用.軌道不平順通過軌道譜描述，并將其視為一個平穩隨機過程.常用軌道譜有美國譜、英國譜和德國譜等.

在有限元模型的求解過程中，需要將軌道譜轉換為時間或空間樣本.本文采用三角級數法[17]生成軌道高低不平順空間樣本，如下所示：

(3)

式中：ω(x)為軌道空間不平順；S(ωk)為選用的軌道不平順功率譜密度函數；ωk為空間角頻率,ωf和ωN為考慮的空間角頻率上下限，由波長和速度確定；Δω為頻率間隔帶寬，該值決定計算精度；x為鋼軌長；φk為對應的第k個頻率的相位，一般為0～2π之間的隨機數[18].

軌道不平順功率譜密度

(4)

式中：Sv(Ω)為軌道不平順功率譜密度，cm2·rad·m-1；K取值0.25；Av為粗糙度系數，取0.033 9 cm2·rad·m-1；Ω為軌道不平順的空間角頻率，rad·m-1；Ωc為截斷頻率,取0.824 5 rad·m-1.通過與本文現場測試軌道運營方提供的軌檢數據比對分析，本文選擇美國六級譜作為輸入激勵.根據上述三角級數法，將式(4)所示的不平順功率譜密度通過式(3)轉換為軌道高低不平順空間樣本，結果如圖6所示.最終，將軌道高低不平順樣本輸入到仿真模型中.

圖6 軌道高低不平順譜Fig.6 Track longitudinal irregularity spectrum

3 模型有效性驗證

通過所建立模型，首先計算獲取斷面I各測點振動響應特性.橋梁的底板(Z4)、腹板(Z5)和翼板(Z6)1/3倍頻程振動加速度級的仿真與測試結果如圖7所示.結果表明，仿真結果與測試結果具有較好的一致性，從而驗證了模型的有效性，滿足本文計算精度要求.斷面I、Ⅱ的計算結果，均與測試結果具有較好的相似性，此處不再贅述.得到驗證的理論模型將用于各層隔振元件性能參數對車-軌-橋系統振動響應特性的綜合影響規律以及參數匹配原則研究.

a 橋梁底板(Z4)

b 橋梁腹板(Z5)

c 橋梁翼板(Z6)圖7 計算與測試結果對比(截面I)Fig.7 Comparison between calculation and measured results (section I)

4 參數影響規律及參數匹配

利用上述理論模型，選取扣件剛度、軌道板支承剛度、橋梁支座剛度3個參數，進行多工況動力學計算.不同參數選取不同水平值，根據實際軌道工程元件性能參數確定上下限，具體數值參見表3.表3中第2行為本文測試斷面Ⅱ各層彈性元件剛度.對表3中參數進行組合，共改變參數48次.計算結束后，輸出各個參數不同水平值下車體、鋼軌、軌道板、橋墩以及橋梁的翼板、腹板、底板振動加速度級.本文現場測試結果表明，除鋼軌振動以外，其余測點優勢頻率主要為低頻范圍，綜合考慮我國城市軌道振動測量及評估相關規范，分析頻率范圍取[0,200] Hz.對計算結果進行整理分析，可得如圖8所示的扣件剛度、軌道板支承剛度、橋梁支座剛度對車體、鋼軌、軌道板、橋墩以及橋梁的翼板、腹板、底板振動特性的影響.本文僅對上述各彈性元件垂向剛度進行影響規律及參數匹配研究.

表3 城市高架軌道多層隔振系統參數Tab.3 Parameter values of multi-layer vibration isolation system of viaduct rail transit

4.1 參數影響規律

4.1.1扣件剛度的影響

扣件剛度的改變對鋼軌振動的影響最為顯著，扣件剛度大幅度降低易于引發鋼軌振動放大，但會改善軌道板以及橋梁的翼板、腹板和底板的振動特性.由圖8a、g可知：扣件剛度對車體及振動向下部和沿線傳遞的影響并不由扣件剛度唯一決定，而是由扣件剛度、軌道板支承剛度及橋梁支座剛度共同決定.當軌道板支承剛度較小時，扣件剛度的降低在一定程度上放大了車體的振動；當軌道板支承較硬時，降低扣件剛度有利于改善車體振動特性.此外，僅當橋梁支座剛度較大時，降低扣件剛度才有利于系統隔振效果，減小傳遞至橋墩和沿線環境的振動能量.反之，會小幅度放大振動能量的傳遞.

4.1.2軌道板支承剛度的影響

降低軌道板支承剛度不僅可以有效抑制振動能量向橋墩，進而向下部基礎結構及沿線環境土體傳遞，同時還對橋梁的翼板、腹板和底板的動力響應具有顯著的有利影響.當軌道板支承變軟時，橋梁的翼板、腹板和底板的振動加速度級均隨之大幅度減小，軌道板支承剛度越小越敏感，影響越顯著.由圖8c可知，由于改變軌道板支承剛度即改變了軌道板子系統的固有頻率，更多頻率成分的振動能量因為軌道板支承剛度的減小而在傳遞路徑中被有效隔離，最終聚集在上部結構中.該部分被隔離的振動能量引發了軌道板自身的振動放大，不論采用小剛度扣件還是較硬的扣件系統，上述放大現象始終存在，而且影響規律不變.由圖8a、b可知，軌道板支承剛度對鋼軌振動的影響較小，對車體的影響需與扣件剛度匹配設計，詳見第4.2節參數匹配原則.

4.1.3橋梁支座剛度的影響

有研究結果表明，當高架軌道橋梁支座剛度在1 000～5 000 kN·mm-1范圍內變化時，剛度的改變對軌道結構的振動幾乎沒有影響[19].在200.43～417.44 kN·mm-1范圍內時，橋梁支座剛度的增加使橋梁結構跨中動力系數減小.橋梁支座剛度由1 927.86 kN·mm-1減小至400.86 kN·mm-1時，橋梁跨中豎向位移隨之增大，最多可增加54%[20].本文對橋梁支座剛度的影響分析結果表明，彈性橋梁支座可有效阻止輪軌作用力及振動能量傳遞至橋墩及沿線環境.當橋梁支座剛度由4 000 kN·mm-1減小至1 800 kN·mm-1時，橋墩振動加速度級最高可降低15 dB，橋梁支座剛度由1 800 kN·mm-1減小至100 kN·mm-1時，橋墩振動加速度級最高可降低35 dB，如圖8g所示.在上述范圍內，橋梁支座剛度的改變并不會對車體、軌道結構和梁體結構的振動響應造成顯著的負面影響，如圖8a～f所示.

4.2 參數匹配原則

上述主要針對單一性能參數的影響規律進行分析，事實上扣件剛度、軌道板支承剛度和橋梁支座剛度對車體和高架軌道結構的影響具有一定的協同和制約關系，需要進行匹配特性研究.

由圖8a可知，隨著扣件剛度和軌道板支承剛度的減小，車體振動響應有所放大.可見，當軌道結構采用超彈性扣件時，車體振動對軌道板支承剛度的變化十分敏感，軌道板支承剛度越小，車體振動響應越大，這種影響規律會隨著扣件剛度的增加而有所減弱.當扣件剛度較大時，軌道板支承剛度的降低反而減小車體振動，因此宜匹配設計小剛度軌道板.此外，當采用高等級浮置板結構時，車體振動隨著扣件剛度的增加而有規律地減小；反之，當軌道板支承剛度較大時，車體振動隨著扣件剛度的增加呈現增大趨勢.橋梁支座剛度幾乎不對上述規律產生影響.由此可見，扣件剛度和軌道板支承剛度具有一定的制約關系，當車體振動響應嚴重時，尤其宜避免小剛度扣件匹配設計小剛度軌道板支承.

由圖8b可知，扣件剛度的改變對鋼軌振動的影響十分顯著，橋梁支座剛度的改變幾乎不影響鋼軌的振動加速度級.當扣件剛度由200 kN·mm-1減小到4 kN·mm-1時，鋼軌振動被放大約9 dB.其中，當扣件剛度在40～80 kN·mm-1范圍內改變時，鋼軌振動對扣件剛度的相關性特征尤其敏感，當扣件剛度小于40 kN·mm-1時，影響趨緩；當扣件剛度較大時，鋼軌的振動加速度級隨著軌道板支承剛度的減小而小幅度降低.扣件剛度和軌道板支承剛度對鋼軌振動的影響規律幾乎不隨橋梁支座剛度的改變而發生變化.綜上，盡管理論上超彈性扣件和低剛度軌道板均可滿足軌道結構較高的隔振需求，但前者極易引發鋼軌的振動放大現象，因此可能導致鋼軌波浪形磨耗及車輪病害等.為滿足系統隔振同時緩解鋼軌振動問題，不宜單獨采用超低彈性扣件作為主要隔振元件，宜適當增大扣件剛度，匹配設計適宜的軌道板支承剛度，使兩者發揮協同作用.

a 車體

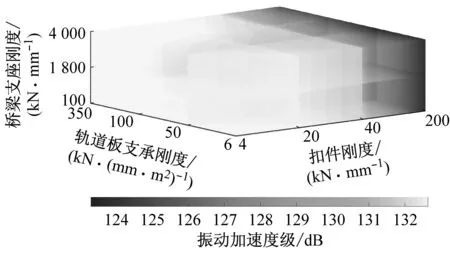
b 鋼軌

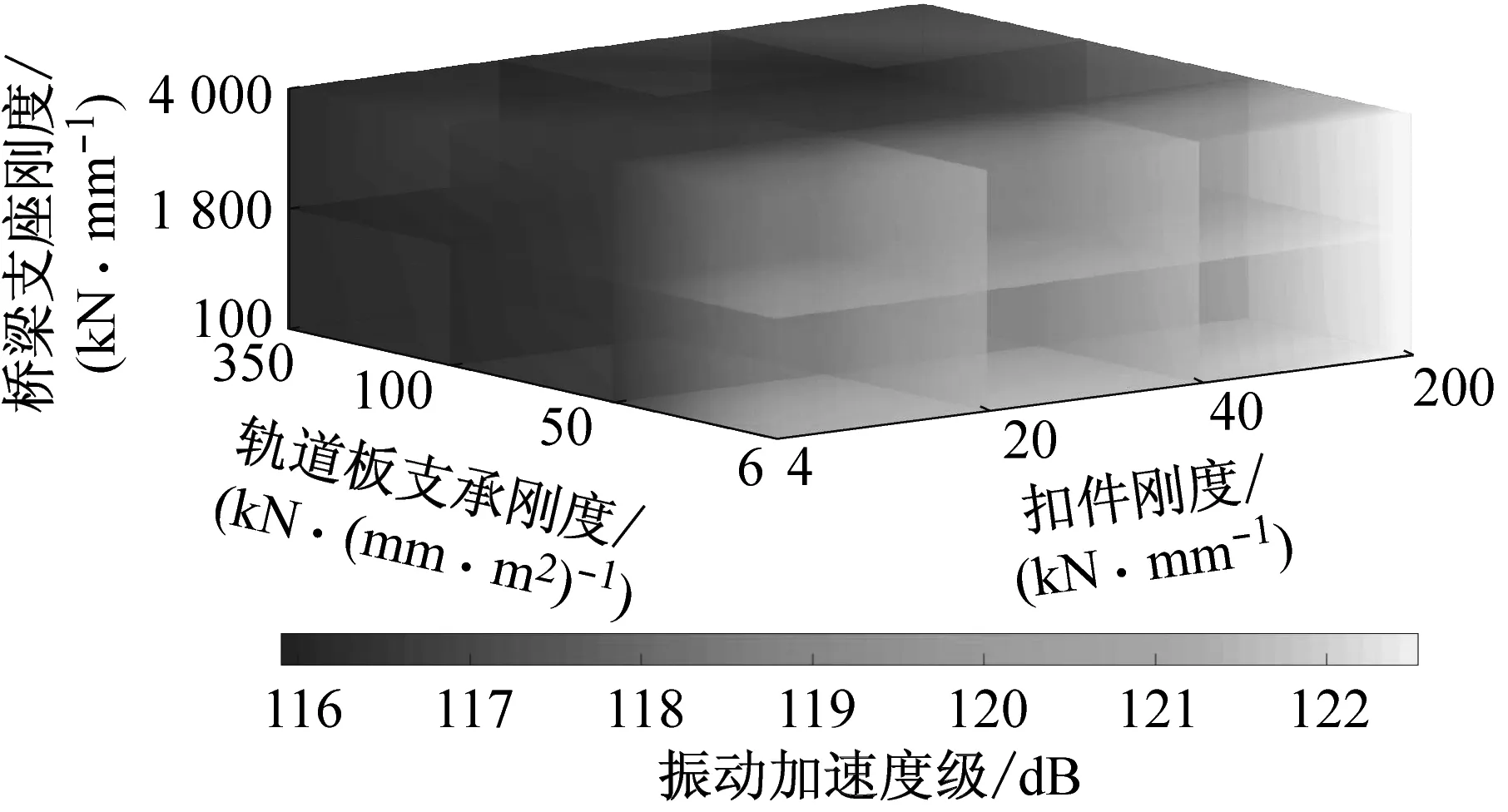
c 軌道板

d 橋梁翼板

e 橋梁腹板

f 橋梁底板

g 橋墩圖8 扣件剛度、軌道板支承剛度、橋梁支座剛度對車軌橋系統各子結構動力響應特性的影響Fig.8 Effect of rail fastener bearing, elastic supporting bearing of rail plate, bridge bearing on dynamic properties of vehicle-railway-bridge system substructures

由圖8c可知，軌道板支承剛度的改變強烈影響軌道板的振動響應，扣件剛度次之，橋梁支座剛度幾乎不影響軌道板的振動.軌道板的振動加速度級隨著軌道板支承剛度的降低而顯著增加，尤其當軌道板支承剛度在6～50 kN·(mm·m2)-1范圍內發生變化時，軌道板的振動響應十分敏感.相反，隨著扣件剛度的減小，軌道板的振動可得到一定程度的改善.軌道板支承剛度和扣件剛度對軌道板振動特性的影響規律不隨橋梁支座剛度的改變而發生明顯變化.由此可見，從改善軌道板振動問題的角度出發，不宜單獨采用超低剛度的軌道板支承結構，如浮置板結構.當軌道沿線具有較高等級的隔振需求時，可考慮匹配設計具有相對較低剛度的扣件來協同實現.

由圖8d～f可知，橋梁的翼板、腹板和底板的振動特性同樣最依賴于軌道板支承剛度，扣件剛度次之，橋梁支座剛度無顯著影響.橋梁的翼板、腹板和底板的振動加速度級均隨著軌道板支承剛度的降低而減小，隨著扣件剛度的降低小幅度減小，兩者具有協同作用.當采用低剛度道床結構作為高架軌道主要隔振措施時，同時匹配設計小剛度扣件，可在滿足隔振需求的同時，進一步改善梁體結構振動響應和低頻輻射噪聲問題.然而，過低的扣件剛度和軌道板支承剛度，可能會引發較嚴重的車體、鋼軌和軌道板的振動放大現象.此外，對比分析圖8d～f可知，當軌道板支承剛度與扣件剛度之比較大時，橋梁的翼板振動加速度級大于腹板和底板；隨著該比值逐漸減小，橋梁的腹板和底板的振動加速度級大幅度降低，翼板的振動改善幅度相對較小.該結論對高架軌道梁體振動、低頻結構噪聲的聲源分析及基于源分析的分源分頻減振降噪措施具有借鑒意義.

本文通過橋墩的振動響應特征表示高架軌道多層隔振系統的綜合隔振效果.由圖8g可知，橋墩結構的振動響應對橋梁支座剛度的變化最敏感，軌道板支承剛度次之，扣件剛度的影響最小.隨著橋梁支座剛度的減小，傳遞至橋墩結構的振動明顯衰減.軌道板支承的小剛度設計也是提高系統隔振效率的有效途徑之一.需要注意的是，當橋梁支座剛度較大時，降低扣件系統的剛度有利于系統隔振，傳遞至橋墩的振動隨之減小；當橋梁支座剛度較小時，降低扣件系統的剛度無益于系統隔振，傳遞至橋墩的振動反而存在一定的放大.可見，在滿足強度、轉動或移動性能、車輛運行安全等前提條件下，采用小剛度橋梁支座是提升高架軌道綜合隔振效率的有效方法之一，并且不會對軌道結構和梁體結構的振動特性產生不利影響.超彈性扣件對低剛度橋梁支座的隔振效果具有一定的制約作用.

5 結論

(1) 扣件剛度的大幅度降低極易引發鋼軌的振動放大，軌道板動力特性對軌道板支承剛度的改變最為敏感，過小的軌道板支承剛度易于引發軌道板較嚴重的振動放大現象.

(2) 扣件和軌道板支承剛度需進行匹配設計，才能有效改善軌道結構柔性設計引發的車體振動響應，以及傳遞至橋墩和基礎結構的振動.

(3) 為改善橋梁的翼板、腹板和底板的振動及振動誘發的低頻輻射噪聲，最直接有效的方法就是合理調節軌道板支承剛度，扣件剛度和橋梁支座剛度的調節無顯著效果.

(4) 相比扣件剛度和軌道板支承剛度，調節橋梁支座剛度是抑制高架軌道振動能量向橋墩及下部基礎傳遞，同時對車體、軌道和梁體結構振動加速度無明顯負面影響的有效方法.

(5) 綜合考慮車體、鋼軌、軌道板、橋梁的翼板、腹板、底板以及傳遞至橋墩和基礎結構的振動響應，當采用超彈性扣件作為系統主要隔振措施時，軌道板支承剛度不宜低于80 kN·(mm·m2)-1.當采用柔性支承軌道板結構作為主要隔振措施時，扣件剛度不宜低于40 kN·mm-1.當采用橋梁支座作為系統主要隔振措施時，不宜匹配設計低剛度扣件系統.