擔(dān)保信用等級(jí)變換的利率互換衍生品定價(jià)
梁 進(jìn), 鄒宏春
(同濟(jì)大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,上海 200092)
自20世紀(jì)80年代初發(fā)生了第一筆互換合約后,互換市場(chǎng)發(fā)展迅猛,金融互換交易已成為目前國際金融市場(chǎng)最大的融資工具之一,其中利率互換和貨幣互換是目前市場(chǎng)上最核心的2種互換工具. 雖然利率互換可以降低資金風(fēng)險(xiǎn)和利率風(fēng)險(xiǎn),但是隨著次貸危機(jī)和歐債危機(jī)的爆發(fā),作為反映受評(píng)對(duì)象違約可能性大小的信用等級(jí),越來越受到人們的關(guān)注.
信用等級(jí)確定的目的在于評(píng)估受評(píng)對(duì)象違約可能性的大小,一般由專門的信用評(píng)級(jí)機(jī)構(gòu)進(jìn)行評(píng)估. 目前國際三大評(píng)級(jí)機(jī)構(gòu)對(duì)信用評(píng)級(jí)的定義基本一致,均認(rèn)為信用評(píng)級(jí)是對(duì)債務(wù)人償債能力和償債意愿的綜合評(píng)價(jià). 三大評(píng)級(jí)機(jī)構(gòu)認(rèn)為:信用評(píng)級(jí)只是對(duì)受評(píng)對(duì)象信用風(fēng)險(xiǎn)的評(píng)價(jià),不是對(duì)其資產(chǎn)價(jià)值的度量,不能單獨(dú)用作投資操作的依據(jù)[1].
目前市場(chǎng)上對(duì)于信用風(fēng)險(xiǎn)的管理主要集中在違約風(fēng)險(xiǎn)上,對(duì)于信用等級(jí)變換風(fēng)險(xiǎn)管理的研究還比較少. 在利率互換過程中,雖然利率作為一種公共因子存在,但是在利率互換這一特定的參考實(shí)體中,利率的高低會(huì)影響到互換一方違約的可能性(如利率下跌會(huì)使得固定利率支付方違約可能性變大),和公司的信用掛鉤,因此定義利率信用等級(jí).利率越低,固定利率支付方公司違約可能性越大,利率信用等級(jí)越低.
國內(nèi)外學(xué)者對(duì)信用等級(jí)變換模型做了許多研究. Jarrow等[2]首次用Markov鏈模型描述信用等級(jí)遷移過程,并給出了在遷移強(qiáng)度為常數(shù)以及回收率為零的情況下公司債券價(jià)格的解析解. 梁進(jìn)等[3]研究了約化方法下信用等級(jí)遷移和違約風(fēng)險(xiǎn)的零息票債券定價(jià),模型中信用等級(jí)遷移強(qiáng)度與利率公共因子有關(guān),在假設(shè)參數(shù)為常數(shù)的情況下得出了每個(gè)信用等級(jí)債券價(jià)值的解析解. 以上都是基于約化模型框架下對(duì)信用等級(jí)變換過程進(jìn)行刻畫,但信用等級(jí)變換與公司資產(chǎn)價(jià)值密切相關(guān),所以采用結(jié)構(gòu)化模型刻畫信用等級(jí)變換比約化方法更加自然直接. 目前為止,通過結(jié)構(gòu)化模型刻畫信用等級(jí)變換的研究比較少. 曾楚琨[4]利用結(jié)構(gòu)化方法討論了具信用等級(jí)遷移的債券定價(jià),分別研究了利率為常數(shù)和隨機(jī)利率情況下的定價(jià). Hu等[5]研究了具信用等級(jí)遷移債券定價(jià)的自由邊界問題,通過結(jié)構(gòu)化方法對(duì)債券定價(jià)并得到了自由邊界問題的一些性質(zhì). Liang等[6]利用結(jié)構(gòu)化方法研究了具信用等級(jí)遷移風(fēng)險(xiǎn)公司債券的效用無差異定價(jià).
針對(duì)目前市場(chǎng)上存在的各種信用問題,投資者們自然想要采用某種手段來規(guī)避自己所面臨的信用風(fēng)險(xiǎn),于是信用違約互換(CDS)應(yīng)運(yùn)而生. 它是一份為特定公司的違約風(fēng)險(xiǎn)提供保護(hù)的合約,特定公司稱為參考公司. 當(dāng)投資者買入?yún)⒖脊景l(fā)行的參考債券時(shí),為減少或避免參考公司違約對(duì)投資者造成的損失,投資者(即CDS買方)會(huì)向交易對(duì)手(即CDS賣方)買入一份CDS合約. 合約規(guī)定,當(dāng)參考公司違約時(shí),交易對(duì)手須對(duì)投資者的損失進(jìn)行賠償,為此投資者須定期向交易對(duì)手支付保費(fèi),直至合約到期或信用事件的發(fā)生. 作為目前市場(chǎng)上最流行的信用衍生產(chǎn)品,CDS研究受到廣大學(xué)者的關(guān)注,研究主要集中在擔(dān)保違約風(fēng)險(xiǎn)的情況[7-9].
對(duì)于利率互換中的違約風(fēng)險(xiǎn)問題,梁進(jìn)等[10]利用約化方法討論了信用攸關(guān)的利率互換的定價(jià),并且對(duì)定價(jià)函數(shù)的性質(zhì)和參數(shù)的依賴關(guān)系進(jìn)行分析. Huang等[11]研究了無違約條款和違約條款的信用攸關(guān)的利率互換的定價(jià),利用歷史數(shù)據(jù)對(duì)參數(shù)進(jìn)行估計(jì)并得出了合約價(jià)值的數(shù)值解.
在結(jié)構(gòu)化方法框架下,本文給出在利率互換過程中擔(dān)保信用等級(jí)的首次遷移所帶來損失的合約定價(jià)模型. 采用結(jié)構(gòu)化方法刻畫利率信用等級(jí)的首次遷移,并且在對(duì)合約價(jià)值的自變量的處理方法中,將低等級(jí)下零息票利率互換的價(jià)值作為合約價(jià)值函數(shù)的自變量. 利用對(duì)沖技巧推導(dǎo)合約價(jià)值滿足的偏微分方程,并且利用計(jì)價(jià)單位轉(zhuǎn)換的方法得到合約價(jià)值的半解析解. 最后,通過對(duì)偏微分方程進(jìn)行數(shù)值模擬得到合約價(jià)值隨時(shí)間變化的關(guān)系圖,并且分析了各個(gè)參數(shù)對(duì)合約價(jià)值的影響.
1 模型的建立
在利率互換中,浮動(dòng)利率支付方支付浮動(dòng)利率,固定利率支付方支付固定利率. 隨機(jī)利率時(shí)時(shí)刻刻都在變化,隨機(jī)利率下跌使得固定利率支付方違約的可能性變大(相對(duì)應(yīng)的隨機(jī)利率上升導(dǎo)致浮動(dòng)利率支付方的違約可能性變大),一旦隨機(jī)利率低于某個(gè)特定值(信用等級(jí)邊界),隨機(jī)利率所遵循的隨機(jī)過程就會(huì)發(fā)生變化. 因此,對(duì)于浮動(dòng)利率支付方而言,采用零息票定價(jià)法計(jì)算得到的利率互換的價(jià)值就會(huì)不一樣,那么就有可能導(dǎo)致浮動(dòng)利率支付方產(chǎn)生損失.
考慮這樣一則合約,其目的是將利率互換過程中信用等級(jí)變換的風(fēng)險(xiǎn)轉(zhuǎn)移給愿意承擔(dān)這份風(fēng)險(xiǎn)的金融機(jī)構(gòu),在合約期限內(nèi),公司A(浮動(dòng)利率支付方)與公司B(固定利率支付方)進(jìn)行利率互換. 公司A面臨隨機(jī)利率發(fā)生信用等級(jí)變換的風(fēng)險(xiǎn),即若利率下跌,則公司B違約的可能性就會(huì)變大,公司B的信用等級(jí)下降. 于是,公司A與另外一家金融機(jī)構(gòu)C簽訂一張合約來規(guī)避利率信用等級(jí)變換帶來的損失,其中公司A為利率保護(hù)買方,金融機(jī)構(gòu)C為利率保護(hù)賣方. 公司A一次性向金融機(jī)構(gòu)C支付保費(fèi),在合約期間一旦隨機(jī)利率發(fā)生信用等級(jí)變換,則合約終止,并且公司A利率互換的損失由金融機(jī)構(gòu)C來支付.
本節(jié)主要從Vasicek利率模型出發(fā),假設(shè)信用等級(jí)只有高低2種等級(jí),并且只擔(dān)保首次發(fā)生信用等級(jí)變換所帶來的損失. 利用結(jié)構(gòu)化方法來定義利率信用等級(jí)遷移時(shí)刻,將低等級(jí)下利率互換的價(jià)值作為合約價(jià)值的自變量,以此來構(gòu)建利率互換過程中利率等級(jí)發(fā)生變換的合約定價(jià)模型.
1.1 基本假設(shè)
作如下基本假設(shè):
(1) 假設(shè)市場(chǎng)是完備的,不存在套利機(jī)會(huì).
(2) 利率產(chǎn)品由一張面值為1、到期日為T的零息票債券構(gòu)成.
(3) 擔(dān)保的是固定利率支付方的信用等級(jí),保費(fèi)由利率信用等級(jí)保護(hù)買方(浮動(dòng)利率支付方)在期初一次性支付給賣方(相應(yīng)的擔(dān)保浮動(dòng)利率支付方也可以做類似考慮).
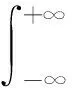
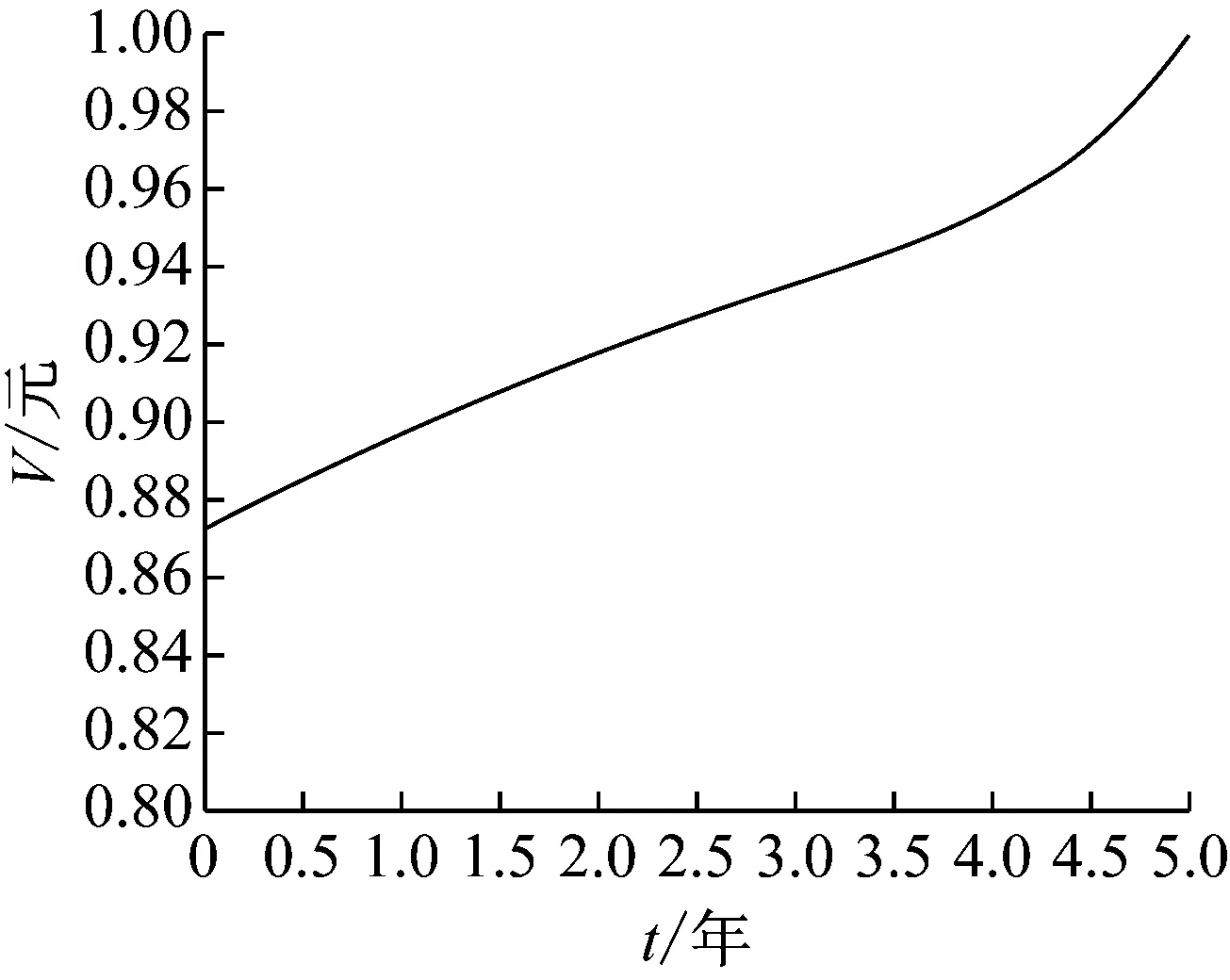
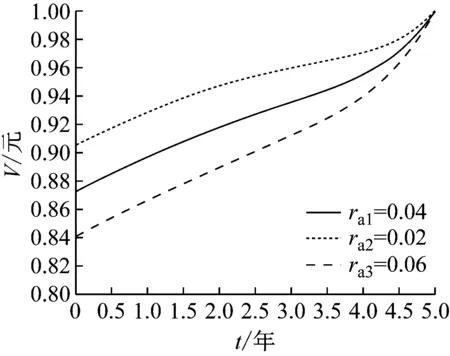
(4) 存在一個(gè)信用等級(jí)邊界ra.當(dāng)隨機(jī)利率r≥ra,利率處于高等級(jí);當(dāng)r (5) 市場(chǎng)利率模型為Vasicek模型,如下所示: drt=a(θ-rt)dt+(σ11{rt≥ra}+σ21{rt 式中:a、θ均為正常數(shù);1A為事件A的示性函數(shù);σ1和σ2為常數(shù),分別表示高、低等級(jí)下波動(dòng)率,有σ1<σ2;{Wt∶0≤t≤T}為由概率空間(Ω,F,Q)生成的標(biāo)準(zhǔn)Brown運(yùn)動(dòng). (6) 合約擔(dān)保的是固定利率支付方信用等級(jí)的下降,并且只考慮擔(dān)保信用等級(jí)的首次遷移. 隨機(jī)利率首次發(fā)生信用等級(jí)遷移的時(shí)刻定義為 τ=inf{t|r0>ra,rt≤ra} 1.2.1零息票定價(jià)公式[12] 若不考慮信用等級(jí)變換,市場(chǎng)利率模型為以下Vasicek模型: drt=a(θ-rt)dt+σdWt 由Feynman-Kac公式可知,在鞅測(cè)度下函數(shù)P(r,t;T)適合以下偏微分方程Cauchy問題: (1) 其中, 上述Cauchy問題有如下形式的仿射結(jié)構(gòu)解: P(r,t;T)=A(t)e-rB(t) (2) 其中, 1.2.2現(xiàn)金流損失分析 由于在信用等級(jí)變換之前并沒有產(chǎn)生損失,損失是由發(fā)生信用等級(jí)變換引起的,因此只需要分析信用等級(jí)變換以后直至到期日的時(shí)間段內(nèi)2個(gè)不同信用等級(jí)下零息票的價(jià)值差. 高、低等級(jí)下利率分別用r1t和r2t表示,相應(yīng)地零息票利率互換的價(jià)值分別為P1t和P2t. 對(duì)于高等級(jí)而言,將低等級(jí)下零息票P2t=P(r2t,t;T)看作一種風(fēng)險(xiǎn)資產(chǎn),由It公式可知[12] 由式(2)可知 同時(shí),由于P2t滿足式(1),立刻可得P2t滿足的隨機(jī)微分方程,如下所示: (3) 若固定利率支付方因隨機(jī)利率下降而在利率互換合約到期日T之前發(fā)生信用等級(jí)變換,變換時(shí)刻為τ,則利率保護(hù)買方(浮動(dòng)利率支付方)將由于固定利率支付方信用等級(jí)變換而產(chǎn)生利差. 若P1τ>P2τ,則利差為P1τ-P2τ;若P1τ≤P2τ,則利差為零. 因此,此時(shí)利率保護(hù)賣方應(yīng)該向保護(hù)買方賠付的金額為(P1τ-P2τ)+. 由于賠付金額的表達(dá)式含低等級(jí)下零息票的價(jià)值P2,因此本文從一個(gè)新的角度對(duì)合約價(jià)值的自變量進(jìn)行定義. 信用等級(jí)一旦發(fā)生變化(從高等級(jí)到低等級(jí)),那么此時(shí)低等級(jí)下零息票對(duì)于高等級(jí)下利率可以看作是一種風(fēng)險(xiǎn)資產(chǎn).式(3)為低等級(jí)零息票價(jià)值滿足的隨機(jī)微分方程.類似于債券和期權(quán)定價(jià)模型[13],將風(fēng)險(xiǎn)資產(chǎn)低等級(jí)下零息票價(jià)值P2作為合約價(jià)值的自變量,把合約的價(jià)值看作是時(shí)間t、高等級(jí)下利率r1和風(fēng)險(xiǎn)資產(chǎn)低等級(jí)下零息票價(jià)值P2的函數(shù). 因此,在t時(shí)刻合約的價(jià)值 下面利用對(duì)沖技巧[13]來推導(dǎo)合約的價(jià)值Vt=V(t,r1,P2)所滿足的偏微分方程. 構(gòu)造投資組合 Πt=Vt-Δ1tP1t-Δ2tP2t 式中:Δ1t和Δ2t分別表示無等級(jí)變換風(fēng)險(xiǎn)高等級(jí)下零息票債券和低等級(jí)下風(fēng)險(xiǎn)資產(chǎn)的份額. 通過選取適當(dāng)?shù)摩?t和Δ2t,使得投資組合在高等級(jí)隨機(jī)利率r1下是無風(fēng)險(xiǎn)的,如下所示: dΠt=dVt-Δ1tdP1t-Δ2tdP2t=r1tΠtdt (4) (5) 其中, (6) 將式(6)代入式(5),則在區(qū)域 有 (7) f(t)=(P1t,ra-P2t,ra)+ P1t,ra=A1(t)e-raB(t),P2t,ra=A2(t)e-raB(t) 式中:Ai(t)(i=1,2)分別為A(t)中σ取σi(i=1,2)的情形. 接下來對(duì)偏微分方程(7)進(jìn)行求解. 偏微分方程(7)是一個(gè)二維偏微分方程. 首先利用計(jì)價(jià)單位轉(zhuǎn)化方法[12]將方程轉(zhuǎn)化為一維問題,然后通過各種變量變換和函數(shù)變換將方程轉(zhuǎn)化為對(duì)拋物型偏微分方程的第一類初邊值問題的求解. (8) 其中, 為了將上述方程(8)轉(zhuǎn)化為一般的熱傳導(dǎo)方程的初邊值問題,作如下變換[13]: 在上述變換下, 方程變?yōu)槿缦滦问? (9) 其中, 方程(9)為拋物型方程第一初邊值問題,作如下變換[14]: z=x-x0,φ(s,z)=u(s,z)-h(s) 代入方程(9)可以求解得到如下形式的解: 其中, 結(jié)合上述變換,有合約的價(jià)值 (10) 其中, 相應(yīng)的定解條件和人工邊界條件為 利用上面的九點(diǎn)顯式差分格式,繼而代回原變量,即得到利率保護(hù)買方的保費(fèi)的預(yù)期支付額. 圖1顯示了保費(fèi)的預(yù)期支付額V與隨機(jī)利率r和時(shí)間t的關(guān)系曲面. 取參數(shù)a=0.5,θ=0.04,σ1=0.04,σ2=0.06,ra=0.04,T=5,時(shí)間步長(zhǎng)τ1=0.05, 空間步長(zhǎng)h=0.01. 圖1 保費(fèi)預(yù)期支付額與隨機(jī)利率和時(shí)間的關(guān)系 Fig.1Variationofexpectedpremiumswithrandominterestratesandtime 圖2顯示了隨機(jī)利率r取定后,保費(fèi)的預(yù)期支付額V和時(shí)間t的關(guān)系. 然而,由圖2并不能說明保費(fèi)隨時(shí)間的增長(zhǎng)而變大. 圖2 保費(fèi)預(yù)期支付額和時(shí)間的關(guān)系Fig.2 Variation of expected premiums with time 圖3顯示了利率回歸速度a對(duì)保費(fèi)的影響,a的大小反映了利率的變化速度.a越大,利率變化越快,保費(fèi)的預(yù)期支付額越小. 從圖3可以進(jìn)一步看出,當(dāng)a很小時(shí),保費(fèi)與時(shí)間的關(guān)系不再是單調(diào)的關(guān)系,這也就解釋了之前的結(jié)論. 圖3 回歸速度對(duì)保費(fèi)預(yù)期支付額的影響Fig.3 Effect of regression speed on expected premiums 圖4顯示了利率回歸均值θ對(duì)保費(fèi)的影響.θ影響了利率最終趨于的值的大小,θ越大,說明隨機(jī)利率最終趨于的值越大,也說明隨機(jī)利率支付者的損失越少,所需支付的保費(fèi)相應(yīng)越少. 圖5顯示了信用等級(jí)變換邊界ra對(duì)保費(fèi)的影響. 由圖5可以看出,ra越大,保費(fèi)的預(yù)期支付額越小. 這是因?yàn)樾庞玫燃?jí)變換邊界越大,在發(fā)生信用等級(jí)變換時(shí)對(duì)于浮動(dòng)利率支付方來說損失就越少,故而保費(fèi)的預(yù)期支付額就越小. 圖5 信用等級(jí)邊界對(duì)保費(fèi)預(yù)期支付額的影響Fig.5 Effect of credit rating border on expected premiums 在利率互換合約實(shí)施過程中,利率下跌造成固定利率支付方信用等級(jí)下降,因此浮動(dòng)利率支付方與第三方機(jī)構(gòu)簽訂一份擔(dān)保合約.通過分析利率信用等級(jí)變換的首達(dá)時(shí)刻以及由于利率互換過程信用等級(jí)下降所產(chǎn)生的利差,給出了合約現(xiàn)金流的表達(dá)式,并且將低等級(jí)下零息票的價(jià)值作為合約價(jià)值的自變量,利用結(jié)構(gòu)化方法推導(dǎo)出滿足合約價(jià)值的二維偏微分方程.通過坐標(biāo)變換和計(jì)價(jià)單位轉(zhuǎn)換將問題化為一般拋物型偏微分方程的初邊值問題,進(jìn)而得到解析解的表達(dá)式. 最后,利用有限差分方法的顯式格式得到問題的數(shù)值解,得出了合約價(jià)值隨時(shí)間變化的關(guān)系圖,并且分析了各個(gè)參數(shù)對(duì)合約價(jià)值的影響.結(jié)果表明,合約價(jià)值與時(shí)間的單調(diào)關(guān)系與參數(shù)a有關(guān),并且與參數(shù)a、θ、ra有著明顯的單調(diào)遞減關(guān)系.1.2 現(xiàn)金流分析

1.3 偏微分方程的推導(dǎo)

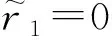
2 模型求解與數(shù)值分析
2.1 偏微分方程求解

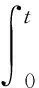

2.2 數(shù)值結(jié)果




3 結(jié)語

