理清概念，把握實質

翟愛國 沙國祥

有人說：學數學就是玩數學概念的．無論多難的題目，最終都會回歸到課本上的基本概念．概念，是我們思維、判斷的細胞！尤其在做錯有關概念的題目后，應及時翻開課本，進一步理解、鞏固基本概念．首先應注重“看”：把課本上與錯題相關的概念完整地看一遍，看清概念是怎樣嚴格而簡練地敘述的，其作用是什么；其次還應注重“想”：想清楚為何要引進這個概念，概念的本質是什么，關鍵詞有哪些；最后更應注重“練”：挑選部分有代表性的、含有這類概念的習題演練一遍，體會如何運用概念解決問題．例如，

下列說法中，正確的有幾個？

（1）周期函數必有最小正周期；

（2）因為cos（π＋1）≠cos1，所以π不是函數y＝cosx的周期；

（3）函數y＝sinx在（0，＋∞）上是周期函數；

（4）周期函數的圖象每隔周期區間長度重復出現．

同學們，你認為有幾個正確？正確答案為3個．（2）（4）的正確性容易判斷．（1）（3）哪個對呢？我們一起回歸課本．課本上函數周期性的概念是這樣表述的：

一般地，對于函數f（x），如果存在一個非零的常數T，使得定義域內的每一個x值，都滿足f（x＋T）＝f（x），那么函數f（x）就叫做周期函數，非零常數T叫做這個函數的周期．

根據函數周期性的定義可知，函數y＝sinx，存在一個非零的常數T＝2π，在定義域（0，＋∞）內的每一個x值，都滿足f（x＋2π）＝f（x），所以函數y＝sinx在（0，＋∞）上是周期函數，因此（3）正確．許多同學出錯的原因是，沒有從概念出發來判斷，而是武斷地認為，如果是周期函數，它的定義域（0，＋∞）的左端不應該是有界限的．其實有些教輔用書上也有關于函數周期性的錯誤結論．比如：周期函數的周期不止一個，若T是周期，則kT（k∈Z，k≠0）一定也是周期．這里忽略了這個結論的前提是函數的定義域必包含元素±T，±2T，±3T，±4T，……但像y＝sinx，x∈（0，＋∞）這樣的函數的定義域并不包含－2π．

（1）對嗎？課本上沒有說周期函數必有最小正周期，實際上并不是所有的周期函數都有最小正周期的．例如，任意的非零常數都是常數函數f（x）＝c（c常數，x∈R）的周期，但因為正數集合中沒有最小者，所以f（x）沒有最小正周期．

一些同學考試時，思維不嚴謹，也會出概念方面的差錯．又如這樣一道題：

函數y＝|tanx|的最小正周期是_________．

有的同學錯解為：

因為函數y＝tanx的最小正周期是π，所以函數y＝|tanx|的最小正周期是

由于受思維定式的影響，有的同學有一種不好的解題慣性：凡是題目相似的，都可以套用結論，不對題目認真分析、感悟題目的細微變化，從而看不清題目中包含的概念或原理的實質．

在學習正切函數的周期性之前，研究過函數y＝|sinx|的周期性，由其圖象可知它的最小正周期是函數y＝sinx最小正周期的一半，由此類比作出推理：y＝|tanx|的周期就是y＝tanx周期的一半．其實這是錯誤的，我們可以作出函數y＝|tanx|的圖象，發現其最小正周期為π，與y＝tanx的周期一樣．錯解引發我們注重思維過程，如本題中借助圖象來澄清周期的概念，而不輕易套用結論．在數學反思中，批判性思維對把握概念的本質有著不可低估的作用．

怎樣才算是透徹理解和靈活運用一個概念？主要是看我們能否將概念進行類比遷移．我們看一個例子：

已知定義域為（0，＋∞）的函數f（x）滿足：①對任意x∈ （0，＋ ∞），恒有f（2x）＝2f（x）成立；②當x∈ （1，2］時，f（x）＝2－x．給出如下結論：

① 對任意m∈Z，有f（2m）＝0；

② 函數f（x）的值域為［0，＋∞）；

③ 存在n∈Z，使得f（2n＋1）＝9；

④ “函數f（x）在區間（a，b）上單調遞減”的充要條件是“存在k∈Z，使得（a，b）?（2k，2k＋1）”．

其中所有正確結論的序號是________．

本題的函數f（x），只給出了一小段區間上的解析式，十分抽象．在不了解題目中數學對象的特點和規律時，如果盲目硬做，勢必如霧里看花，水中望月．因此，現在解題的大方向是：了解這個函數，找出其特點和規律．

仔細觀察，可以發現條件①f（2x）＝2f（x）很像周期函數的條件f（x＋2）＝f（x），因此，我們可以將周期函數的概念進行類比遷移．類似于周期函數，由一個周期中的函數值和函數性質可以推知其他周期中的函數值和函數性質．借助條件②，根據已知的一個小區間上的函數表達式，由近及遠，推而廣之，探尋規律．

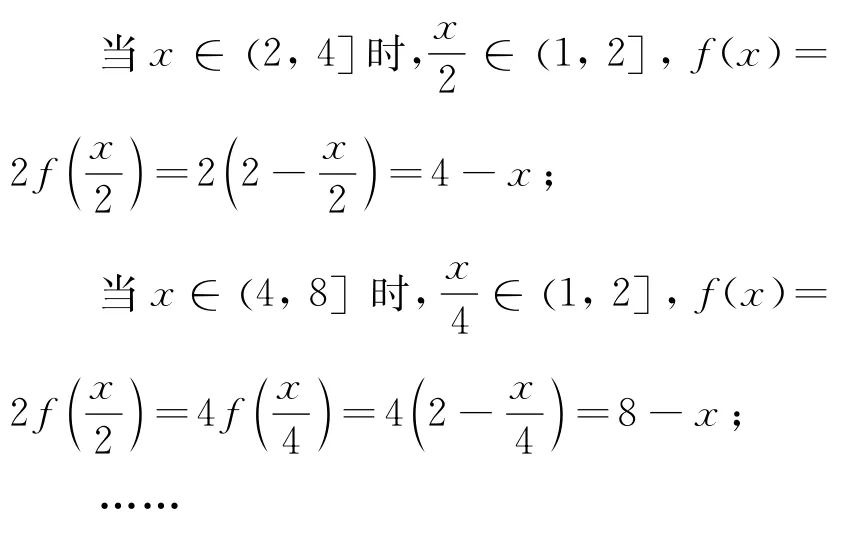
由此，我們找到規律（一般模式）：

當x∈（2m，2m＋1］時，f（x）＝2m＋1－x，其中，m＝0，1，2，…

如果我們作出f（x）的圖象的草圖（請你自己作），則更可以把f（x）的真面目看得真真切切、明明白白！由此不難判定正確答案是①②④．

在復習知識時，還要理清概念之間的聯系，把握哪些概念是基本的、核心的，哪些概念是派生的．例如，

（根據湖北省高考試題改編）定義在（－∞，0）∪ （0，＋∞）上的函數f（x），如果對于任意給定的等比數列｛an｝，｛f（an）｝仍是等比數列，則稱f（x）為“保等比數列函數”．現有定義在 （－∞，0）∪（0，＋∞）上的如下函數：

①f（x）＝x2；②f（x）＝2x；③④f（x）＝ln|x|．

則其中是“保等比數列函數”的f（x）的序號為________．

這道題把函數概念、等比數列概念融為一體，揭示了二者的聯系，同時引入了一類新的函數的概念：“保等比數列函數”．

初見此題，你會對其中的新概念覺得陌生，其實只要以第①個函數f（x）＝x2探路，它相當于問：已知等比數列｛an｝，則各項平方后所得數列是否為等比數列？呵呵，原來不過如此！這類題目你一定做得很多，關鍵是運用等比數列的概念去判斷；又如第③個函數也可保數列等比性不變；由第④個函數f（x）＝ln|x|生成的數列｛ln|an|｝則是等差數列，一般不是等比數列，由此可以真正理解為何等比數列與等差數列有很多類似的性質，它們通過對數概念和對數運算的性質密切聯系在一起；第②個函數也可根據新的概念推知不是“保等比數列函數”．這里，要充分理解函數概念的本質與作用：“對應”，更準確地說是“變換”，即給出一個等比數列，對所有項進行平方（或開方、取對數）等變換，得到一些新數列，其中有些新數列還是等比數列，有些則不是．本題要求考生對函數、數列、對數的概念、作用以及幾種基本初等函數的性質有深刻的理解，并具有綜合運用函數、數列知識解決問題的能力．

柏拉圖說：“優秀是一種習慣．”好的思維習慣使人終身受益．希望同學們能養成用概念思考的習慣！