熱管當量熱導率的實驗研究

項祖康，夏耀廣，陳慷華

（海軍工程大學動力工程學院，湖北武漢 430033）

0 前言

近年來，隨著微∕納電子技術的飛速發展，電子元件表現出朝著大功率，高集成，小體積的發展趨勢，這也導致電子元件功率密度的急劇增大，對散熱能力提出了更高的要求[1-2]。熱管作為一種高效的傳熱元件，它所呈現出來的優勢使其在電子元件散熱領域有著廣闊的應用前景，它對于提高系統的散熱能力、減小電子元件散熱系統的體積和重量、提高設備抗惡劣環境的能力等都有著積極的作用[3-7]。由于電子元件設備時常處于變工況狀態，傳統上認為普通熱管的當量導熱率不變的處理方法在實際的變熱負荷應用中可能會導致大的溫度偏差，影響設備的正常運行。

基于以上問題，本文探索一種變熱負荷的情況下熱管當量熱導率的測試方法，分析熱管熱導率隨功率增加的變化規律，并擬合它的當量熱導率函數表達式，為熱管冷卻系統熱設計及其在電子元件設備的實際應用奠定基礎。

1 實驗原理

本文將熱管熱阻獨立以建立數學模型來研究，視熱管為一維導熱體，采用經典的傅立葉導熱定律來解決問題。假設熱量完全由熱管以導熱的形式傳遞到熱沉，用熱管的有效長度Leff來代替導熱體厚度δ，用熱管蒸發段和冷凝段外表面溫度代替熱管的橫截面上的平均溫度[8]。根據實際電子元件的發熱功率對熱管賦予不同的熱負荷，得到相應熱負荷下的當量熱導率λi，將各熱負荷工況下得到的λi繪成曲線，就得到了它的變化規律，公式推導如下：

其中：

λi——當量熱導率，（W∕m·℃）；

A——熱管橫截面積，m2;

Qi——發熱功率，W；

Tei——熱管蒸發段溫度，℃；

Tci——熱管冷凝段溫度，℃。

本實驗采用的熱管為哈爾濱晨怡熱管廠DH32-004型熱管，如圖1所示。采用T型熱電偶和數據采集器作為測溫設備，在熱管熱源至熱沉沿途均勻分布；以發熱電阻絲模擬電子元器件作為熱源，通過滑動電阻控制發熱功率；熱沉處采用風扇強迫對流散熱。

圖1 熱管實物圖Figure1 Thephysical map of theheat pipe

2 實驗過程

將各實驗組件正確連接，固定發熱元件和熱管鋁板，并用導熱硅膠促進其導熱。在熱管的蒸發段和冷凝段分別布置3個T型熱電偶，用數字標簽對每個熱電偶進行標注。對ADAM溫度采集系統進行程序調試，正確設定各個參數，如冷端補償、采樣頻率等。安裝風道，使風道只對準熱沉，避免其對絕熱段和蒸發段產生影響。利用萬能表對直流電源電壓進行檢查，觀察是否為24 V。調節滑動變阻器，觀察電流的可控范圍，計算發熱功率的可調范圍，確定是否能控制在10～60 W的范圍。整個裝置如圖2。

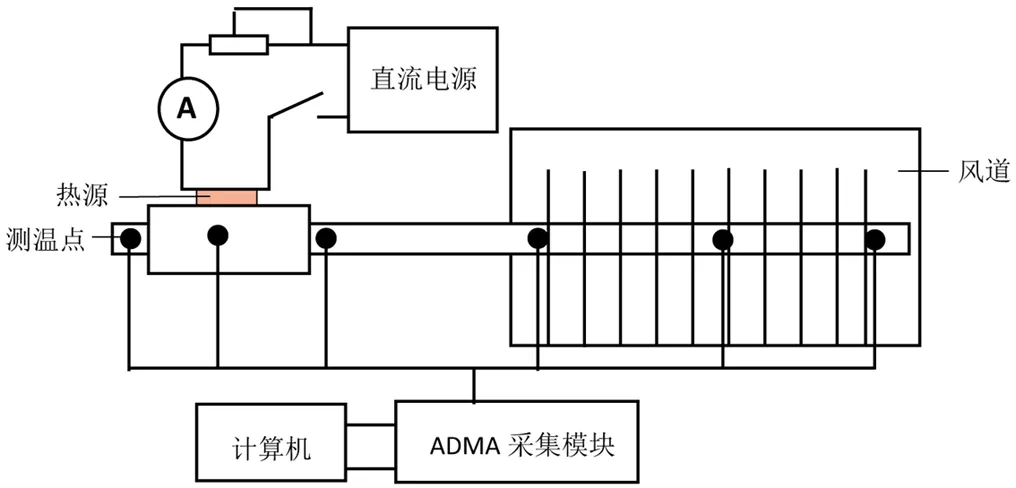
圖2 實驗裝置圖Figure2 Experimental setup

實驗平臺搭建完畢后，實驗將按照如下步驟進行：

（1）測量熱管直徑和長度，用于最后的熱導率的計算；

（2）測試在沒有風冷卻熱沉的情況下，不同發熱功率時熱管蒸發段和冷凝端溫度，并記錄；

（3）測試風速風量，確定建立高風速的冷卻熱沉環境；

（4）測試在高風速冷卻熱沉的情況下，不同發熱功率時熱管蒸發段和冷凝端溫度，記錄數據并繪制圖像。

3 實驗系統與數據處理

將不同發熱功率時熱管蒸發段和冷凝段在高風速冷卻熱沉、環境溫度為27.6℃的工況下測得的數據放在Origin中處理可得到圖3。圖3顯示隨著加熱功率的不斷增大，熱源、蒸發段、冷凝段溫度不斷增大，但蒸發段和冷凝段的溫度增長速率并不相同，以致兩者的差值不斷增大。根據傳熱學原理，在熱負荷不斷增大的條件下，普通熱管兩端的溫差會相應增大，以此來增大傳熱量。假設這是標準的平壁導熱體，那么熱阻是不變的，在熱負荷增大的情況下，導熱元件只能依靠增大溫差來增強傳熱。

圖3 熱源、蒸發段、冷凝段溫度隨功率的變化規律Figure3 The varying law of the temperature of heat source part，evaporating part and condensating part alongwith thepower

由圖4可見，溫差隨著功率的增大而不斷增大。但圖4同時顯示，溫差并沒有隨著功率的增加而呈線性的增加，而是隨著功率的變大，溫差增加變緩。這說明當量熱導率是變化的。在其他條件不變的情況下，由于溫差的增加變緩可以得出一個結論，即熱管的當量熱導率是隨著發熱元件發熱功率的增大而增大的。

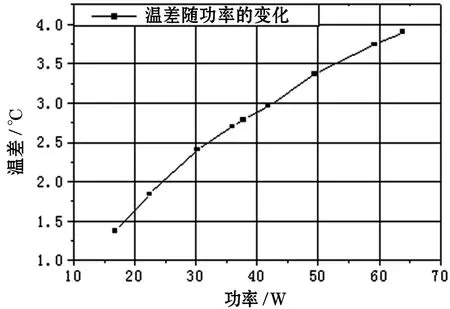
圖4 溫差隨功率的變化Figure4 Changesof the differencein temperaturealongwith thepower

由圖5可見，熱管在發熱元件低發熱功率工況下當量熱導率的變化較小，而當發熱功率加到35 W后當量熱導率增長加快，且在40 W之后基本呈線性增長。由圖6所示，將熱負荷的變化分作兩部分：在大于35 W且小于正常工作熱負荷下，當量熱導率變化加快，且近似呈線性增長。用Origin數圖處理軟件來進行線性擬合，如圖7所示。

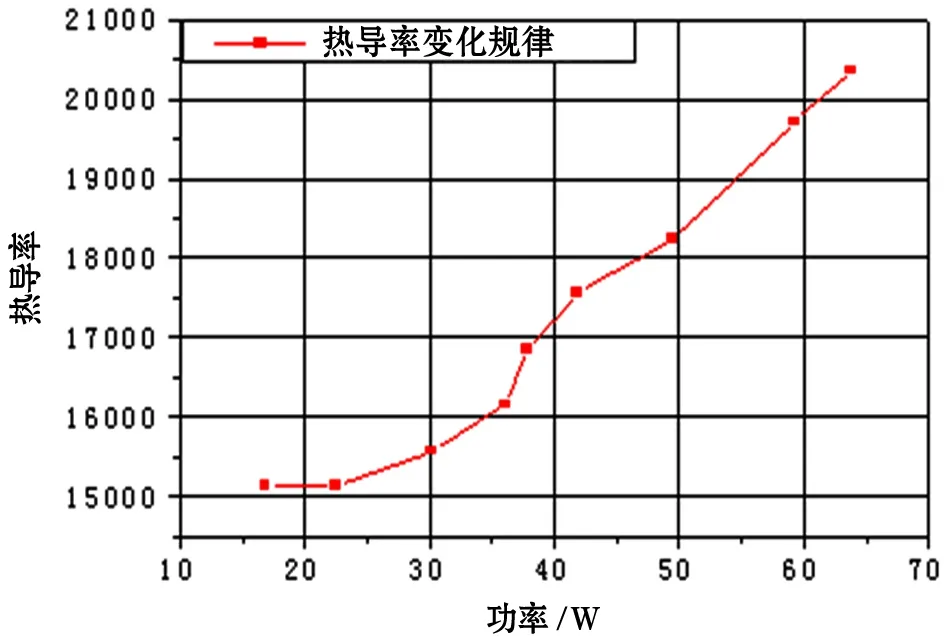
圖5 熱導率隨功率的變化規律Figure5 Thechangesof heat conductivity alongwith thepower

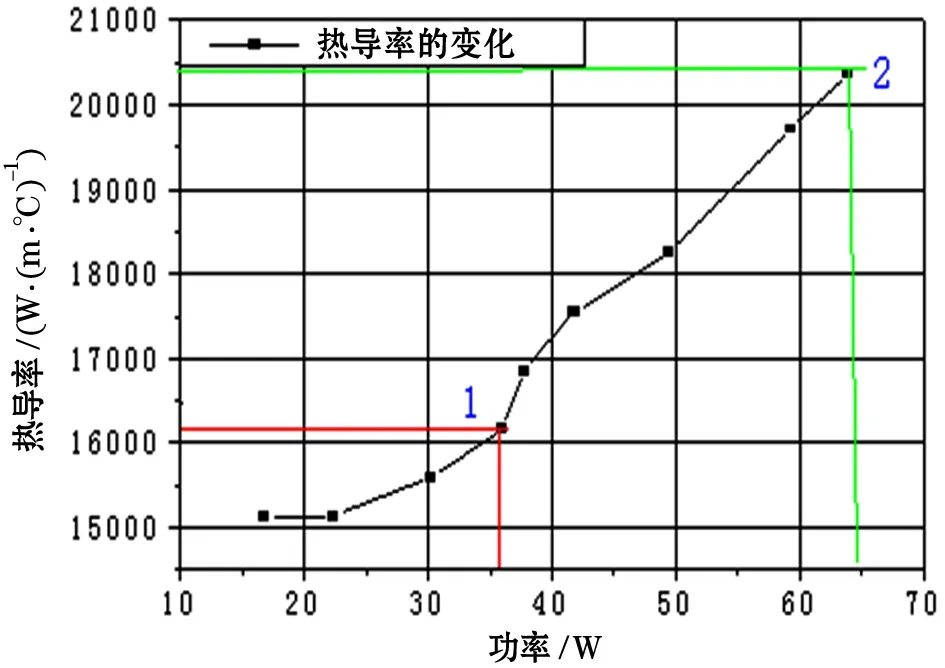
圖6 分段比較熱導率的變化Figure6 Sectional comparison of thechangeof thermal conductivity

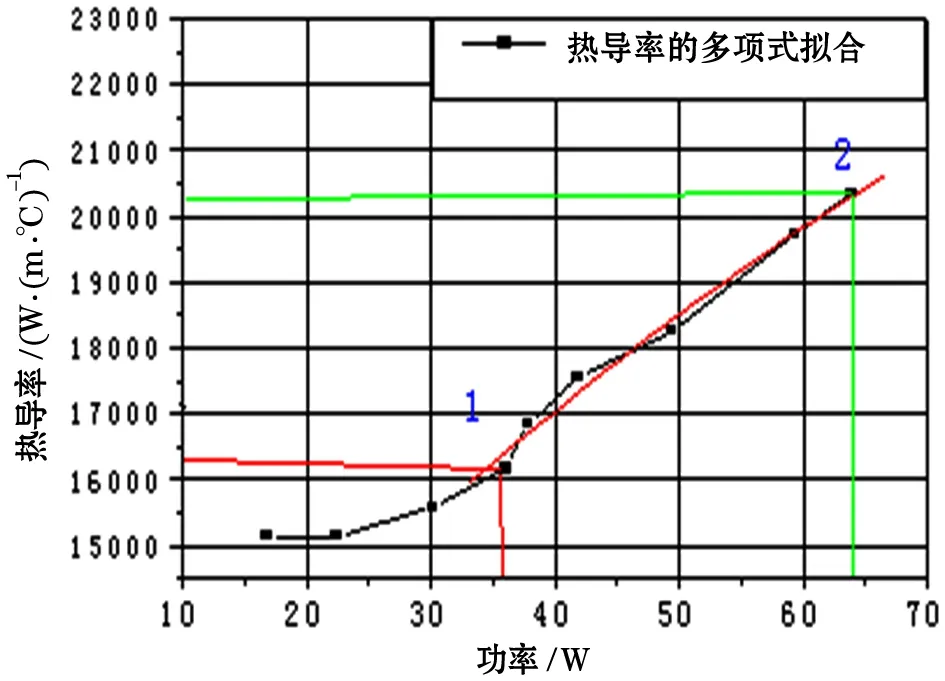
圖7 高熱負荷工況熱導率的線性擬合Figure7 Linear fitting of thermal conductivity under high heat load conditions

根據處理結果，可以得到在較高工況下的當量熱導率變化關系式：

它可以用于當量熱導率的近似估計，也可用于特定試驗的參考數值，如熱管仿真研究中當量熱導率的參數設置。

上述實驗結果分析表明：熱管的當量熱導率在變熱負荷的情況下是變化的，具體來說是隨著發熱元件發熱功率的增加而變大；同時與冷凝端的熱沉設計和冷卻方式有關，冷卻效果好則當量熱導率變化小。而傳統理論在一般研究和基本應用中認為熱管的當量熱導率不變，這對于散熱要求很高的電子元件的熱設計將會造成較大的溫度偏差。

4 總結

本文采用實驗的方法對熱管當量熱導率進行了研究，為熱管在電子元件散熱的實際應用提供了參考，具體結論如下：

（1）熱管的當量熱導率會隨著電子元件熱負荷的增大而增大，并且冷凝段的冷卻效果會顯著影響熱管當量導熱率，因此提高熱管的冷卻效果能改善熱管工作的穩定性；

（2）建立了熱管當量熱導率隨電子器件熱負荷的依變關系，方便將熱管的散熱能力作為單一參數用于系統仿真；

（3）將熱負荷、冷卻強度與熱管的當量熱導率建立雙參數的函數關系將是后續研究工作。