基于擴展卡爾曼濾波的車用鋰離子電池SOC估算

何忠霖，彭憶強，郭威,席林

(西華大學汽車與交通學院，四川成都 610039)

0 引言

隨著國家對環保的要求越來越嚴，督查力度愈來愈大，不少系統和設備開始采用鋰離子電池作為能量的主要來源。鋰離子電池具有能量密度大、功率密度大、自發放電率低、無記憶效應等優點。荷電狀態(State of Charge， SOC)作為電池管理系統(Battery Management System， BMS)中均衡各單體電池的重要參數，在動力電池的使用過程中，易受到內外各種不確定因素的干擾，發生復雜電化學反應的鋰離子電池又是典型的非線性系統。因此，如何利用電池可測參數數據，如電流、電壓、溫度、自放電率、循環充電次數等，通過適當算法來實現當前電池剩余電量準確估算，一直以來是BMS的核心問題和亟需解決的技術難點。為適應需求，許多估算方法應運而生。文獻[1]中提出了安時積分法，并分析了安時積分法估算SOC存在的誤差及解決方案；文獻[2]中提出了開路電壓法，并得到了開路電壓法不適于SOC在線實時估算的結論；文獻[3]中提出了有效質量法，通過測量電池電解液有效質量估算SOC值，但該法只適用于能直接測量電解液質量的鉛酸電池，對于純電動汽車主要使用的鋰離子電池，并不具備使用價值。基于現代控制理論而提出的SOC估計策略在近年來得到了長足發展，其中主要的方法有卡爾曼濾波法、神經網絡法、狀態觀測器法等[4]。其中，神經網絡估算和模糊控制法由于難度大，還停留在計算機仿真研究階段，距離實際運用還有不少路要走。

電池組電量一般是按照電池模組總電壓來進行估算和矯正的，如果電池組的不一致性很大，將會使SOC估算精度誤差增大。具有代表性的是韓國亞洲大學和先進工程研究院，研究人員在對鎳氫電池SOC估算過程中，提出了考慮自恢復效應、自放電效應及老化效應對電池容量的影響[5]，并提出SOC計算公式：

SOC(%)=100%×(實際容量+自恢復效應恢復電量-自放電效應放電量-老化效應損失電量+充電量-放電量)/額定容量

(1)

該公式考慮了伴隨電池使用導致的老化效應，存放過程中的自放電效應和充、放電結束時的自恢復效應對電池電量的影響，計算所得SOC精度相對較高。

對于電動汽車，SOC估算準確與否在很大程度上取決于電池本身壽命長短。同時，SOC也作為電池最基本信息之一提供給駕駛者。因此，SOC估算是BMS中的重點和難點。

為適應鋰電池復雜電反應機制，本文作者在卡爾曼濾波的基礎上，通過將擴展卡爾曼濾波(EKF，Extended Kalman Filter)和復合電池模型結合，搭建了基于EKF原理下SOC估算的仿真模型。文中的創新點在于考慮到復合電池模型的輸入參數為充、放電電流和電池溫度，添加了與電池溫度有關的容量校正模型和與庫侖效率有關的電流效率模型，實現對SOC估算的校正，增加模型估算精度。

1 擴展卡爾曼濾波

1960年卡爾曼在時域狀態空間理論基礎上提出了卡爾曼濾波，隨著計算機系統的發展，卡爾曼濾波逐漸應用到控制系統的各個領域。在卡爾曼濾波中，狀態方程表示相鄰時刻狀態變量的變化規律，輸出方程對部分或全部狀態變量進行觀測，從而實現系統狀態變量的最優估計，即由初始化、估測估計及最優估計三部分構成。

標準卡爾曼濾波常用于線性動態系統，其狀態空間模型如下：

狀態方程：

xk+1=Akxk+Bkuk+wk

(2)

輸出方程：

yk=Ckxk+Dkuk+vk

(3)

式中：uk為系統的輸入量，輸入量是電池溫度和電流；xk為狀態變量，代表SOC值；yk為輸出量，指電池負載電壓，也稱端電壓；vk為過程噪聲，描述狀態轉移過程中的加性噪聲及誤差的過程噪聲變量；wk為觀測噪聲，表示測量系統輸入量時產生的噪聲和誤差，由于vk、wk均為高斯隨機白噪聲，在計算的過程中無法知道實際值，故將其假設為零；Ak、Bk、Ck、Dk為方程匹配系數，用來體現系統動態特性。

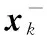
鋰離子電池性能受到溫度、電壓、電流等多種因素的影響，在使用過程中是典型的非線性系統，應采用擴展卡爾曼濾波對電池組SOC進行實時估算。擴展卡爾曼濾波是通過系統狀態空間模型將動力電池非線性系統進行線性化，然后再利用標準卡爾曼濾波算法的原理對狀態變量做最優估計。系統狀態空間模型如下：

狀態方程：

xk+1=f(xk,uk)+wk

(4)

輸出方程：

yk=g(xk,uk)+vk

(5)

式中：f(xk,uk)為非線性轉移函數；g(xk,uk)為非線性測量函數。相對于標準卡爾曼濾波，擴展卡爾曼濾波用f(xk,uk)替代了Akxk+Bkuk，用g(xk,uk)替代了Ckxk+Dkuk。為方便理解，給出如圖1所示的方框圖。

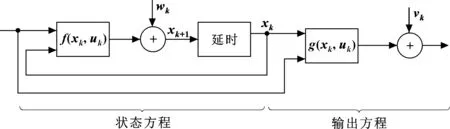
圖1 非線性離散時間狀態模型

具體計算過程如下：

(6)

(7)

狀態變量的真值無法直接測得，因此只能通過間接的方法通過計算得到，必然存在誤差。擴展卡爾曼濾波正是將存在的誤差利用最小均方差原理讓最優估計經過有限次后收斂于真實狀態值。因此，EKF計算后結果收斂的準確性與初值無關，初值僅決定收斂所需時間，而模型的精確性決定收斂結果精度。

(8)

(9)

式中：Dw是過程噪聲wk的方差,會讓均方估計值增加并且會增加狀態估計值的不穩定性。

(3)卡爾曼濾波增益Lk：

(10)

式中：Ck為匹配系數，用來體現系統動態特性；Dv是觀測噪聲vk的方差。卡爾曼濾波增益又叫信噪比平衡因子。當狀態變量處于比較穩定時，修整幅度較小，Lk值較小，反之Lk值較大，修正幅度較大。由公式(10)可以看出，當觀測噪聲增大，Lk值會減小，導致調整幅度減小。

(11)

(12)

當觀測變量yk測量結束后，采用標準卡爾曼濾波對狀態變量、均方估計誤差的預測估計值進行修正，從而得到狀態變量、均方估計誤差的最優估計值。

2 電池模型

文中以某磷酸鐵鋰單體電池模組作為研究對象，基本參數如表1所示。對于擴展卡爾曼濾波，從非線性轉移函數f(xk,uk)、非線性測量函數g(xk,uk)和狀態變量的角度出發，可以分為復合模型、簡化模型、帶滯后效應模型、極化效應修正模型。雖然復合模型精度不及帶滯后效應模型和極化效應修正模型，但計算較為簡單且易于微控制系統實現，所以文中選擇復合模型進行模型搭建。模型總體框架如圖2所示。

表1 某磷酸鐵鋰電池模組參數

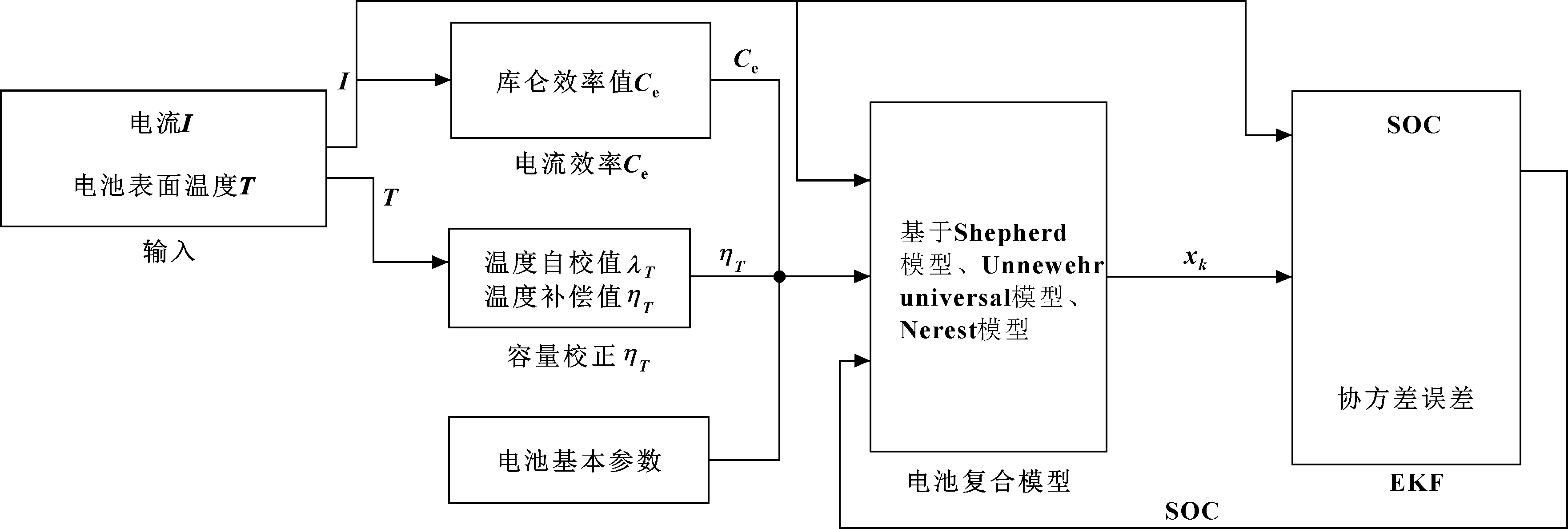
圖2 系統結構框圖

2.1 復合模型

復合模型是基于Shepherd模型、Unnewehr universal模型、Nerest模型組合得到[7]。

狀態方程：

(13)

輸出方程：

(14)

式中：ηT為溫度對電池容量的補償系數；ηI為庫侖效率對電池容量的補償系數；R為電池內阻，會隨溫度和充、放電狀態變化；Ki為電池極化電阻，K1、K2、K3、K4是利用最小方差原理得到，為電池相關匹配參數。

2.2 溫度對電池容量校正模型

電池內部溫度是影響電池容量的重要因素。溫度較高時，電池活性增加，能量得到更有效地發揮，但若電池在高溫環境下長時間工作，會讓電池中的電解質和某些活性物質發生不可逆轉的化學反應，從而導致電池內部晶格被破壞，壽命明顯地縮短。溫度較低時，電化學反應速率降低，電池活性明顯降低，溫度過低時電解液甚至可能凍結，極化效應明顯，電池內阻增加，電池很難充滿電，實際可用容量減少，電池能量利用效率下降。

電池內部溫度對SOC的影響主要有以下兩點：(1)非線性特性。溫度對SOC的影響是非線性的，無論大小，都不能用簡單的線性關系進行描述。(2)溫度對電池容量的影響是非固定的。因此，需要通過試驗得到不同溫度下的容量補償系數。以某單體磷酸鐵鋰電池為研究對象，在滿電(45 A·h)情況下，分別將電池置于-20、-10、0、 25、 40、60 ℃的溫度下，以標稱放電倍率C/30對電池進行放電到截止電壓，通過實驗可得到各溫度下電池的實際容量，通過與標稱容量比較，可得到不同溫度下的容量補償系數ηT：

(15)

式中：QTi為實際容量；QTI為標稱容量。

具體數據如表2所示。

表2 不同溫度下的補償系數

由于所測點溫度分別為-20、-10、0、 25、 40、60 ℃，其為離散點，不能為除所測點外的其他溫度提供容量校正值。因此，將所測實際容量與對應溫度進行曲線擬合，為其他溫度下的容量校正提供支撐，如圖3所示。

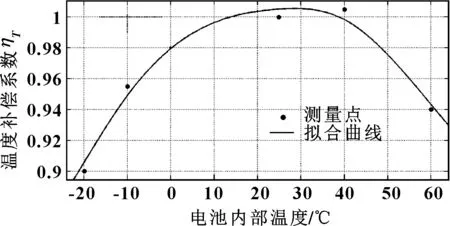
圖3 內部溫度對電池容量校正擬合曲線

一般電池測量溫度為電池極柱溫度，由于電池在生產過程中由于本身構造、使用材料以及裝配方式等不同，導致電池內部溫度和電池極柱溫度有差異，所以需對所測電池溫度進行自校。在滿電并以C/30倍率進行放電，直至截止電壓，如表3所示。

表3 不同溫度下的自校系數

為得到除測量點外其他溫度的自校系數εT，將表3所測數據進行曲線擬合，如圖4所示。

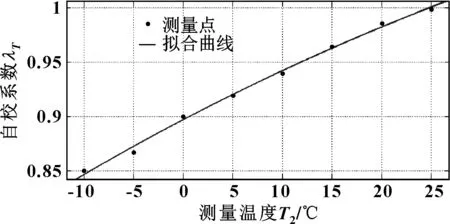
圖4 溫度自校系數擬合曲線

2.3 電流效率模型

電流效率模型主要與庫侖效率有關。庫侖效率又叫放電效率，是指在同一循環過程中放電容量和充電容量的比值。與磷酸鐵鋰電池不同的是，鎳氫、鎳鎘蓄電池具有一定的耐過充能力，因此均衡策略常被設計為正限制。隨著電量增加，磷酸鐵鋰電池的庫侖效率會逐漸降低，過充的電能大部分轉化為熱能消散了。而磷酸鐵鋰電池的庫侖效率一般能達到90%，應在建模過程中考慮該電池庫侖效率變化對電池容量的影響。磷酸鐵鋰在實際使用過程中，充電過程一般是先恒流充電，充到截止電壓后再恒壓充，最后進行涓流充電，充電模式較為固定。因此，庫侖效率主要考慮放電倍率的影響。設置充、放電條件：在25 ℃條件下，充電倍率為0.5C(22.5 A)，分別以0.1C(4.5 A)、0.5C(22.5 A)、1C(45 A)、1.5C(67.5 A)、2C(90 A)、3C(180 A)放電倍率進行放電至截止電壓，如表4所示，可得到不同放電倍率下的容量補償系數，即庫侖效率ηI：

(16)

式中：Qti為實際放電容量；QtI為實際充電容量。

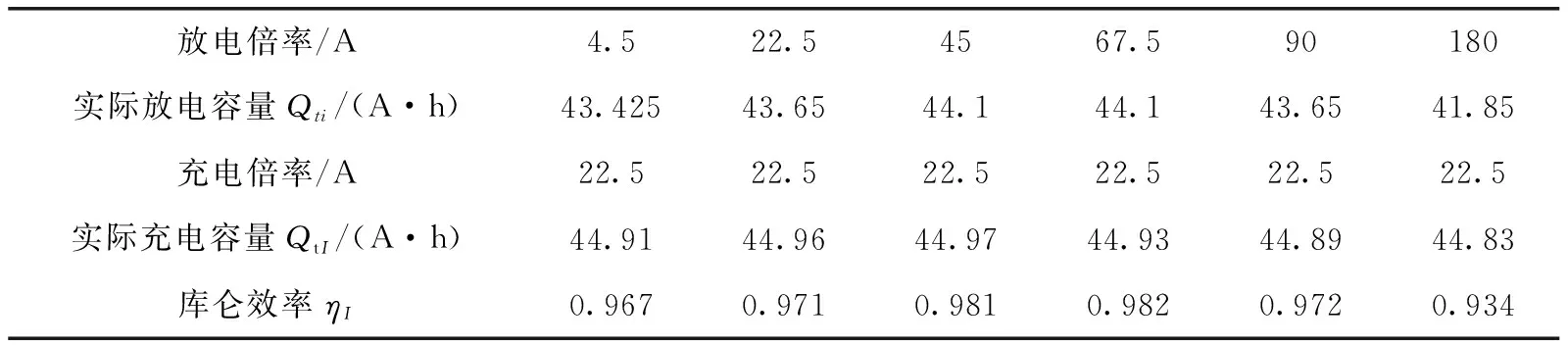
表4 不同放電倍率下的庫侖效率

同理，為得到不同放電倍率下的庫侖效率ηI，將表4中測量點擬合，得到如圖5所示曲線。

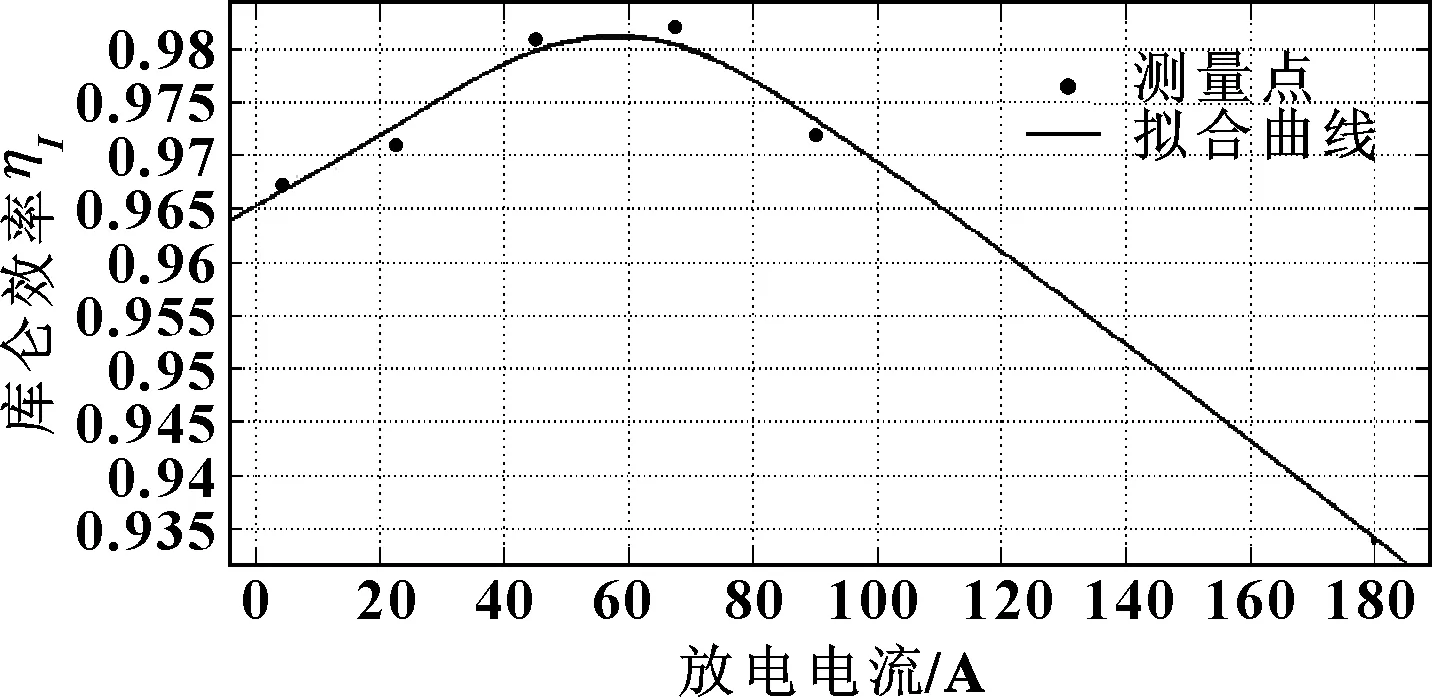
圖5 庫侖效率擬合曲線

3 仿真結果分析

模型搭建完成后，為考慮充、放電倍率對該算法SOC估算的影響，選擇在常溫(25 ℃)下，分別對該模型以1C、3.4C進行恒流放電，靜置一段時間后，再分別以1C、3.4C進行恒流充電、放電，如圖6—圖7所示。下面將截取一部分數據，來驗證文中所提算法的精確性。

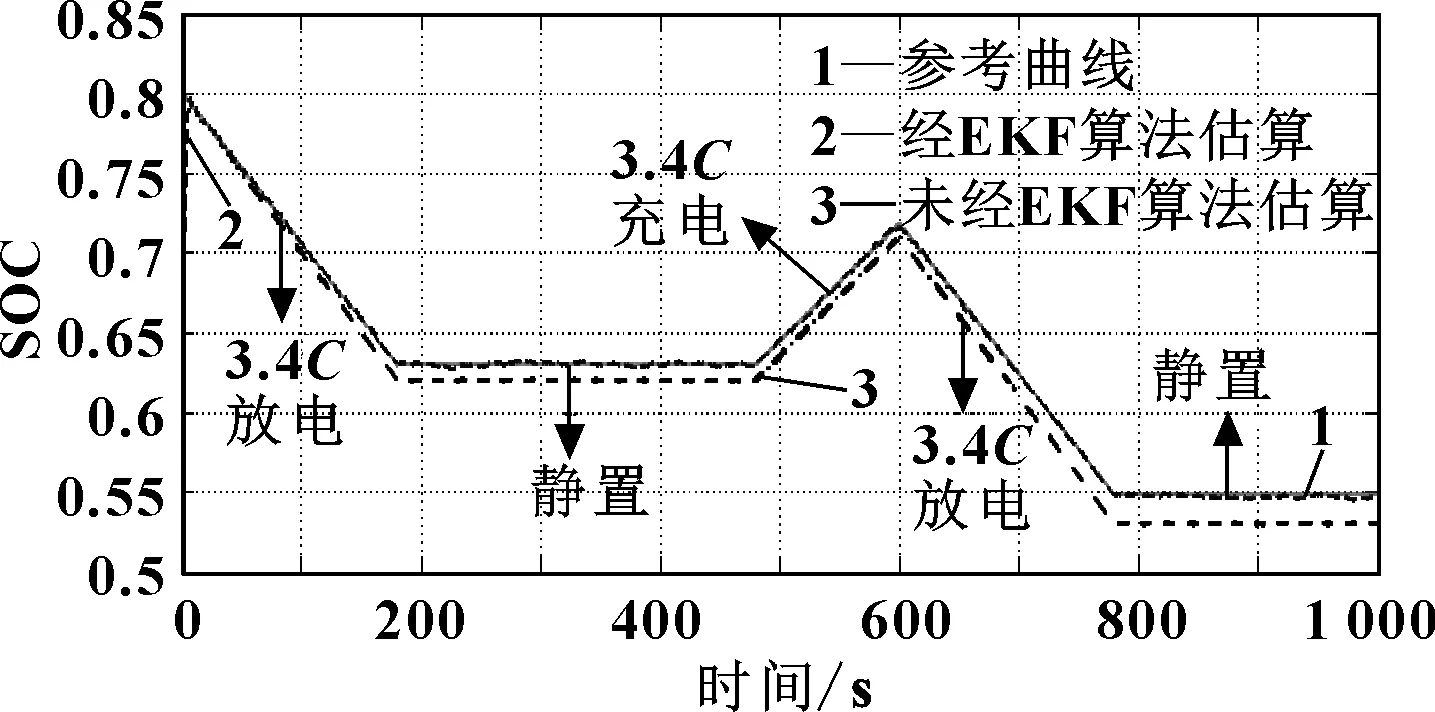
圖6 25 ℃，3.4C充、放電倍率下SOC值曲線圖

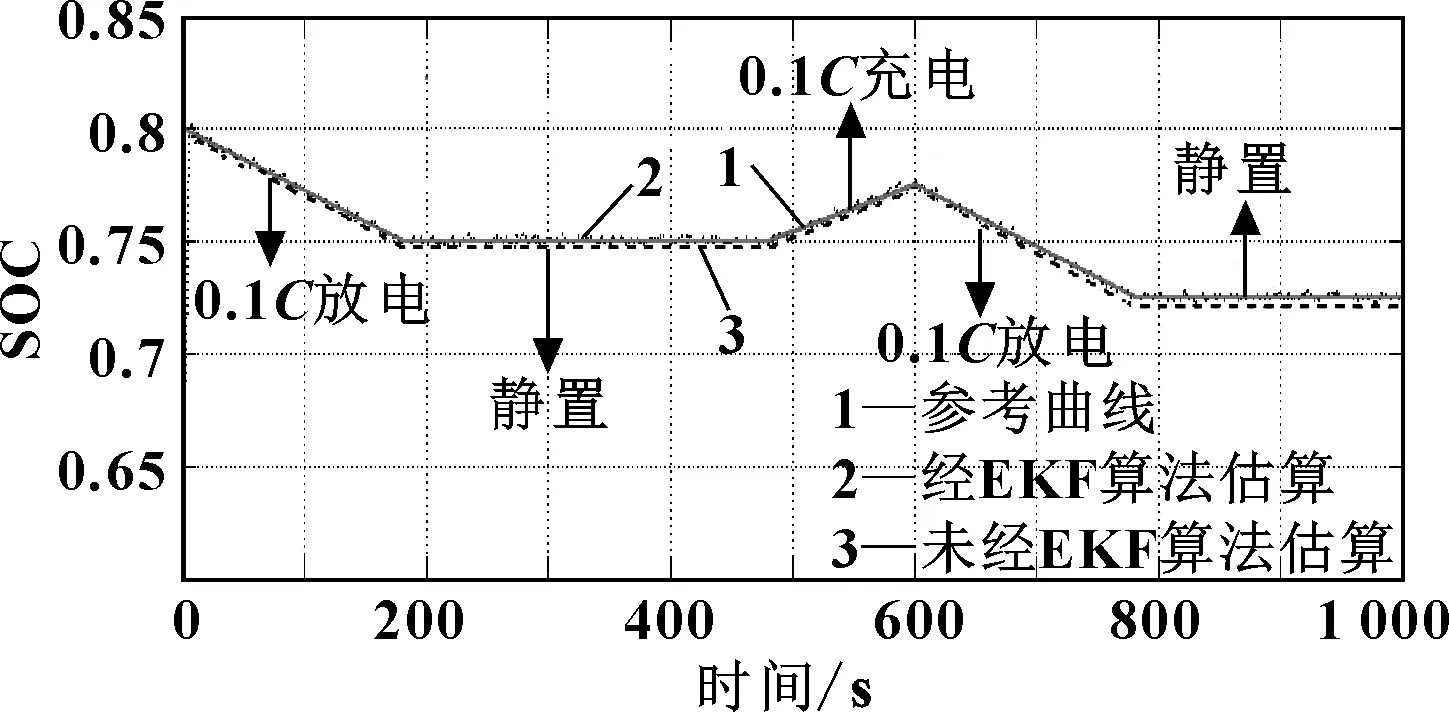
圖7 25 ℃，1C充、放電倍率下SOC值曲線圖

將1C充電倍率下的SOC曲線圖局部放大，如圖8所示。

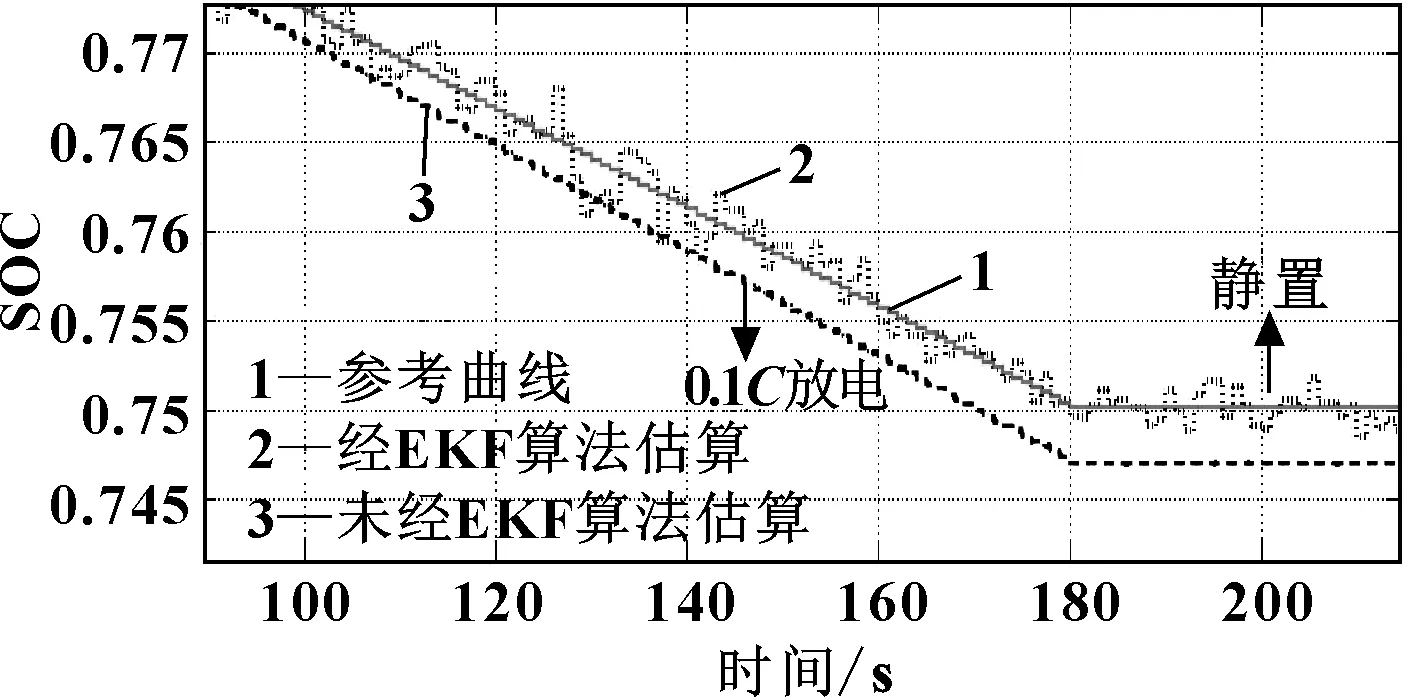
圖8 25 ℃，1C充、放電倍率下SOC值局部放大圖

曲線1為通過安時積分法得到的曲線。因為充、放電過程均為恒流充電、放電，因此，以這條曲線作為參考曲線，且賦予SOC初值SOC0為80%。曲線2是以EKF作為基礎，結合復合電池模型，并經過容量修正、溫度校正后得到的輸出曲線。曲線3是以電池模型作為基礎，以SOC值作為狀態變量，未經EKF直接輸出SOC估算曲線。

通過將不同充、放電倍率下的SOC輸出值比較，不難發現，隨著充、放電倍率增大，未經EKF的SOC估算輸出曲線距參考曲線距離逐漸增大，誤差逐漸增大。而無論是在1C倍率下，還是在3.4C倍率下，EKF輸出曲線始終圍繞參考曲線上下波動，隨著均方誤差逐漸減小，其值最終會收斂于參考曲線。且在這兩種充、放電倍率下，EKF算法估算得到的SOC值比未經EKF、由電池模型直接得到的SOC估算值精度要高。體現了EKF算法的精確度高，穩定性好。

為驗證溫度對模型算法的影響，選擇在3.4C充、放電倍率下，分別以-5、25 ℃進行充、放電，如圖9所示。

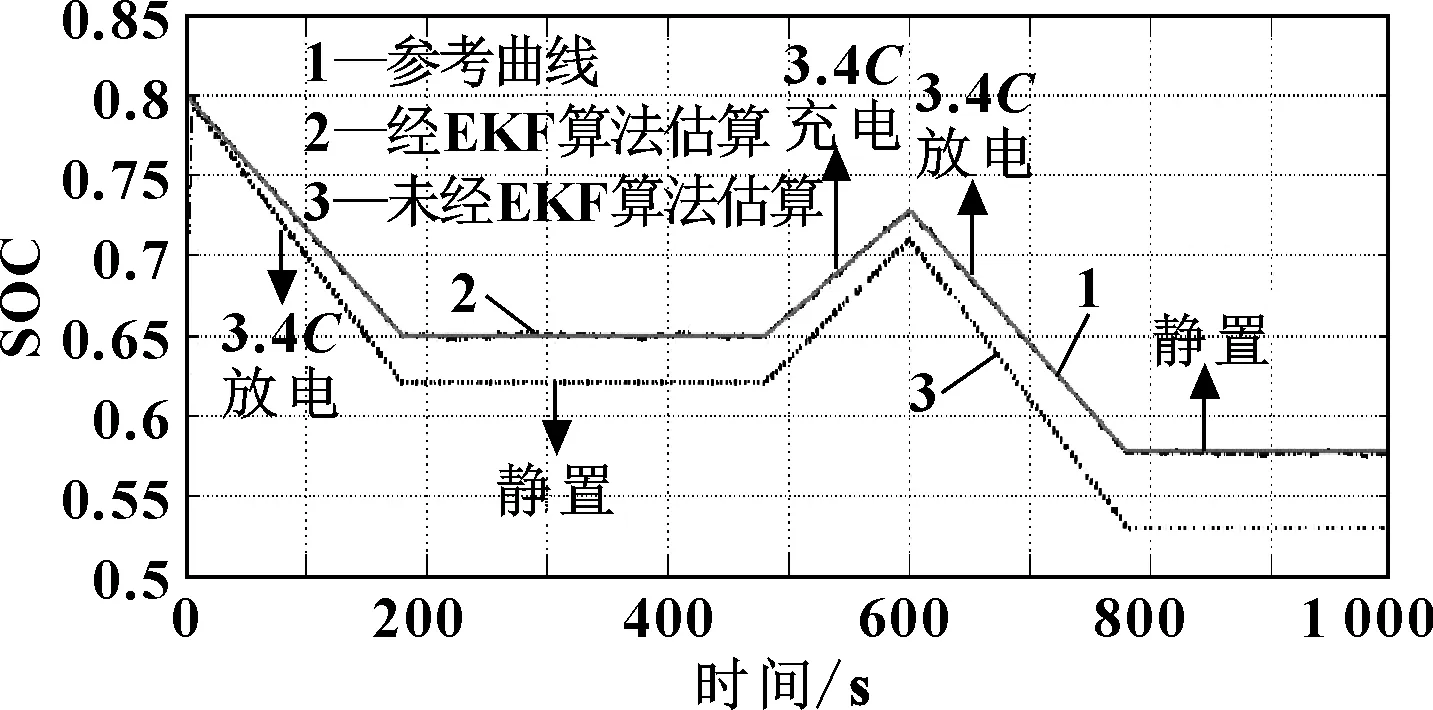
圖9 -5 ℃，3.4C充、放電倍率下SOC值曲線圖

通過圖6和圖9可以明顯看出，溫度對該算法影響很大，-5 ℃下未經EKF算法輸出曲線與參考曲線誤差較大，將近達到4%，而經EKF算法得到的SOC輸出曲線在該環境下誤差較小，經計算最大為0.5%，還存在圍繞參考曲線來回波動的調節過程。說明EKF算法在極端環境中精確度較高，魯棒性較好。

無論是以安時積分法為基礎輸出曲線，還是以電池模型為基礎輸出曲線，都需要賦予S0C初值SOC0，而EKF原理輸出曲線的收斂性與初值SOC0無關。在EKF中，初值的準確與否只關系到算法的收斂時間，所賦初值和實際值之差的絕對值越大，收斂時間越長，反之越短。輸出SOC曲線變化規律不會受到初值影響，屬于EKF算法的優越性。

電動汽車在行駛過程中存在加速超車情況，此時電池需大倍率放電，因此以25 ℃，3.4C倍率放電為主要研究對象。如圖6所示，所選擇的數據范圍為0.520 7～0.8。在開始放電階段，卡爾曼濾波設置的初始值x0為0.630 5，與初值SOC0相差較大，根據卡爾曼濾波原理，為使均方誤差最小，曲線迅速上升，在t=6 s時第一次與參考曲線相交，此時卡爾曼濾波算法預測結果幾乎接近于SOC真實值。隨后無論是在充、放電階段，SOC預測曲線都在參考曲線附近上下擺動，在預測范圍內多次穿越參考曲線并與之反復相交，說明模型精度高，反饋響應及時。但最終預測曲線并不會與參考曲線貼合，而是始終在其周圍小幅震蕩。原因如下：

(1)噪聲矩陣對算法精度的影響。由于無法測量過程噪聲和觀測噪聲真實值，將其假定為零，勢必造成系統噪聲在參數統計過程中存在誤差，導致噪聲參數設置不準確，反饋響應存在誤差[8]。

(2)在充、放電過程中，由于電池極化效應影響，電池參數如電阻等會不斷變化。在建模過程中，為保證算法的實用性和模型的難易度，舍棄了模型中極化效應修正部分，導致電池極化效應對模型響應產生影響。

而另外一條曲線雖能反映SOC變化趨勢，但始終位于參考曲線下方，因為復合模型和系統原模型還存在偏差，在對等效模型進行更新時，由于遲滯效應導致復合模型和真值產生偏差，系統噪聲為有色噪聲，并不為零[9]。

圖10為輸出結果SOC絕對誤差曲線圖，曲線1為經EKF的絕對誤差，計算開始后，真實初值SOC0和EKF中所賦初值存在偏差，根據卡爾曼濾波原理，均方誤差逐漸減小，算法中SOC值向真值逐漸靠攏。誤差曲線迅速向零靠近。SOC值在真值附近小幅震蕩，因此誤差值在零附近小幅震蕩，且最大誤差不超過0.5%，精度比較高。

曲線2是未經EKF濾波，經過復合模型后直接輸出的SOC值的誤差曲線，相對考慮容量校正、溫度校正等的EKF誤差曲線而言，誤差相對較大，當t=600 s后，誤差逐漸增大，整個過程都沒有來回震蕩的調節過程。EKF算法優越性展現無遺。

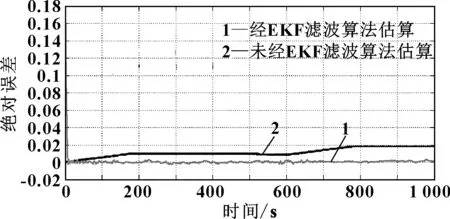
圖10 25 ℃，3.4C倍率下SOC絕對誤差曲線

4 結束語

本文作者以卡爾曼濾波為理論基礎，結合復合電池模型，提出了基于擴展卡曼濾波的鋰離子電池SOC估算方法，并添加了與電池表面溫度有關的容量校正模型以及和庫侖效率有關的電流效率模型，實現對SOC估算的校正。在MATLAB/Simulink中建立上述仿真模型，并對輸出曲線進行分析。通過將經過EKF算法估算和未經EKF算法估算得到的SOC輸出曲線進行比較，表明該算法估算精度較高，誤差較小，且具有來回震蕩的調節過程、抗干擾能力較強的優點。對于SOC估算的實際應用具有一定的參考價值。