基于并行卡爾曼濾波的車輛環境感知方法
涂巖愷,張東風,林明,曹輝標
(1.廈門雅迅網絡股份有限公司,福建廈門 361008;2.鄭州宇通客車股份有限公司,河南鄭州 450016)
0 引言
智能汽車是一個集環境感知、規劃決策、多等級輔助駕駛等功能于一體的綜合系統。它能使車輛在行駛過程中具有實時感知自身狀態及所處地理環境的能力,能夠為汽車的智能化動力性、安全性或經濟性控制決策提供有力的參考依據。載荷與地理坡度是汽車智能優化控制最為依賴的感知量,目前針對載荷進行車輛優化控制的方法有發動機多態控制[1]、路徑優化[2]等,針對地理坡度優化控制的方法有自適應巡航[3]、發動機功率控制[4]等,還有綜合載荷與地理坡度的自動駕駛技術[5]。
傳統的車輛環境感知都是基于傳感器[6-7]的測量,但是高精度傳感器面臨成本高、易損壞、不易維護的問題。目前國外開始研究運用軟件算法分析發動機和儀表往車輛總線上發出的實時數據推算出車輛當前載荷或所處地理坡度的方法。D KIM等[8]提出一種利用汽車縱向動力學關系和迭代最小二乘法的車身質量估算方法,但該方法易受坡度的影響。SEBSADJI等[9]提出利用擴展卡爾曼和龍伯格觀測器結合的坡度估算方法,但是該方法以車身質量已知為前提,在實際商用車使用條件下,車身載荷的變化是非常大的。綜合來看,目前缺少比較準確的能同時求解載荷與坡度的方法。
本文作者提出利用車輛CAN總線上的動力數據,采用分步驟方式先對狀態方程進行差分來抵消相鄰狀態的坡度因素,并采用多組卡爾曼濾波器并行迭代處理,根據收斂結果誤差最小的標準,來選擇一組濾波器求解車輛總質量,之后再根據所求解的車輛質量利用縱向汽車模型來實時估算汽車所處的地理坡度。
1 系統數學模型
汽車縱向動力學模型如圖1所示,汽車在行駛過程中同時受到外部力和內部力的作用。外部力包括空氣阻力Fair、滾動阻力Frolling和重力Fgravity;內部力包括發動機輸出的旋轉扭矩經過傳動系到達車輪上的前進驅動力Ftractive,以及傳動系統的內部損耗。
根據圖1所示的汽車縱向動力學模型,假設m表示汽車總質量,a為汽車加速度,則汽車的力學平衡關系:
Ftractive-Fair-Frolling-Fgravity=ma
(1)
汽車動力傳動系統模型如圖2所示。包括發動機、離合器、變速器、主減速器、車輪。發動機輸出扭矩為Te,傳動到離合器輸出軸的扭矩為Tt,變速箱輸出軸扭矩為Tf,輪軸扭矩為Tw。
發動機輸出到變速器的扭矩Tt:
(2)
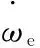
(3)
式中:It是傳動慣性;it是傳動擋位比;Tf是通過變速器后的輸出扭矩。Tf通過主減速器,最終轉化為輪軸上的驅動扭矩Tw:
(4)
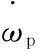
(5)
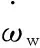
(6)
車輛的加速度可以表示成車輪的旋轉加速度乘以車輪的半徑:
(7)
綜合上述公式可以得到牽引力的表達式:
(8)
式中:ug=itf/rw。
汽車行駛時縱向空氣阻力:
(9)
式中:ρair是空氣密度;Cd是空氣阻力系數;A是車正面的面積。
汽車行駛時的縱向滾動阻力:
Frolling=frmgcosθ
(10)
式中:fr是滾動阻力系數;g是重力加速度常量;θ是道路坡度。
汽車行駛時由坡度帶來的阻力:
Fgravity=mgsinθ
(11)
將公式(8)—(11)代入到公式(1)中,并且令βr=cos[arctan(fr],整理可得到:
(12)
式(12)可視為一個描述發動機輸出扭矩、車速與質量、坡度關系的非線性方程。后續將該方程作為狀態方程,聯立觀測方程,采用卡爾曼濾波迭代的方法,利用連續采集的車輛CAN總線動力數據(包含扭矩Te和車速v)對汽車總質量和坡度求解。
2 狀態方程與求解
令Ts為車輛兩個狀態的時間間隔,v表示車輛速度,下標k表示狀態序號,基于式(12)建立基于車輛速度的狀態方程如下:
(13)
如果直接采用擴展卡爾曼濾波方法同時迭代求解式(13)狀態方程中的坡度和質量參數,容易陷入錯誤收斂。例如當車輛行駛在無坡度的平原地區時,因為無地形變化來糾正誤差,有可能迭代收斂得出質量偏重地形長下坡、或質量偏輕地形長上坡的錯誤結論。文中提出將狀態方程進一步差分、分步求解的方法,先利用多組卡爾曼濾波器進行并行計算,取收斂后預測噪聲最小的一組濾波器的質量作為車輛當前質量,再反推車輛所處的地理坡度。因為車輛總線上速度信號和扭矩信號的發送頻率非常快,前后兩個信號周期一般在100 ms以內,因此,前后兩個狀態的坡度和道路阻力系數近似相等,即:α2φ2,k≈α2φ2,k-1,因此將式(13)前后兩個狀態相減,令Xk=vk-vk-1,整理可得抵消掉坡度參數只含質量參數的狀態方程:
Xk=AXk-1+BUk+Wk
(14)
式中:A=1;B=Ts;
觀測量即為車輛當前的縱向加速度,因此觀測方程:
zk=HXk+Vk
(15)
式中:觀測矩陣H=1;Vk為觀測噪聲,方差為R。Pk表示信號協方差,即信號的預測誤差。建立卡爾曼迭代方程組如下,其中ε取一個常數初始值開始迭代:
(16)
上述迭代方程組是對車輛加速度的預測求解,且方程組中的質量參數未知,不能直接進行運算,需要有一個預設質量值。由于商用車輛的車型參數中具有空載的整備質量me與最大允許總質量mz兩個參數,因此實質的載重質量應該介于me與Mz之間。在me與mz之間每100 kg取一個質量值,作為式(16)迭代方程組中的質量參數,這樣一共有N=(mz-me)/100組卡爾曼迭代方程組進行并行計算。N組卡爾曼濾波器各自獨立進行迭代運算,如圖3所示。
取所有運算結果為收斂的濾波器,比較收斂后Pk的大小,Pk越小,表示使用當前質量對于加速度的預測誤差越小,說明該質量參數最符合車輛運行的動力模型,取該組卡爾曼濾波器對應的質量值為車輛當前總質量。求得車輛質量參數后,將質量代回公式(12)即可由車輛的扭矩信號Te及加速度a計算車輛當前所處坡度值。
3 實驗結果
采用ZK6876H5Z型號客車進行實驗,整備質量為4 300 kg,最大允許質量為6 100 kg。實驗時經過裝載負重,實際整車質量為5 543 kg。由于比較難去測繪準確的道路地理坡度,因此將車輛置于汽車轉鼓實驗臺上進行實驗,如圖4所示,所需地理坡度可直接在轉鼓實驗臺上設置,將文中的環境感知算法計算得到的坡度與轉鼓所設地理坡度比較,以驗證數據的準確性。
從整備質量4 300 kg開始,每100 kg取一個質量代入式(16)卡爾曼濾波器組,一共有19組濾波器并行進行迭代計算,每組濾波器ε取一個相同常數初始值,進行了200輪迭代后,共有4組濾波器收斂,15組濾波器不收斂。收斂的4組濾波器Pk值關系如圖5所示。
可以看到,5 500 kg對應的卡爾曼濾波器迭代收斂誤差最小,因此取5 500 kg為載重計算結果。得到質量之后,進一步反推車輛所處的坡度。將利用式(12)反推出的車輛所經過的地理坡度和轉鼓設置的坡度進行對比,結果如圖6所示,可以看出二者有比較高的重合度,說明此方法估算的地理坡度有比較高的準確性。
4 小結
文中通過車輛的縱向動力學關系,在建立基于速度的狀態方程基礎上,進一步進行差分處理,建立基于加速度的卡爾曼迭代計算方程,利用汽車總線信號頻率高間隔短的特點,先約去卡爾曼濾波器中的坡度參數,將質量參數分段代入濾波器組中,利用并行卡爾曼濾波器組迭代計算,選擇收斂后誤差最小的濾波器組對應的質量為估算的車輛質量,之后再反推坡度。實驗證明:該方法有比較高的準確性,可直接利用車輛總線信號估算車輛環境參數,減少了利用傳感器的成本,使車輛能夠實時感知當前所處內外部環境狀態,能有效提高車輛智能化水平。

