淺談“線性規(guī)劃問題”常見題型及其求法
■重慶市鐵路中學校 何成寶
線性規(guī)劃是運籌學的重要分支之一,也是高中數學教材中的重要內容之一,解題步驟是由已知條件寫出約束條件,并作出可行域,進而通過平移直線在可行域內求線性目標函數的最優(yōu)解。下面對線性規(guī)劃常見的幾類題型舉例說明,希望對同學們的學習有所幫助。
一、已知線性約束條件,求線性目標函數的最值問題
例1若x、y滿足約束條■件則z=x+2y的最小值是( )。
A.6 B.2 C.3 D.5
解:如圖1,作出可行域。將直線l:x+2y=0向右上方平移,當過點A(2,0)時,有最小值2,故選B。
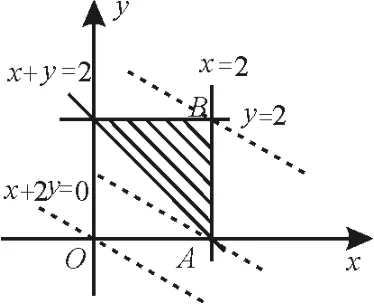
圖1
點評:解決線性目標函數的最值問題,常將目標函數z=a x+b y轉化為直線的斜截式:,通過求直線的截距的最值,間接求出z的最值。
變式訓練1:設變量x、y滿足約束條件的最大值為解:畫出可行域,如圖2所示。分析可得在直線2xy=2與直線x-y=-1的交點A(3,4)處,目標函數z取得最大值18。
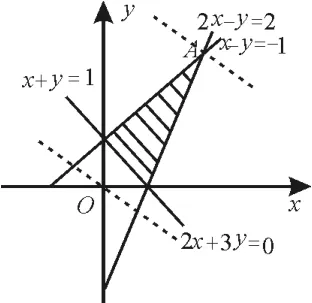
圖2
二、已知線性約束條件,求非線性目標函數的最值問題
例2已知x、y滿足以下約束條件則z=x2+y2的最大值和最小值分別是( )。
A.13,1 B.13,2
解:如圖3,作出可行域。x2+y2是可行域內的點(x,y)到原點的距離的平方,故最大值為點A(2,3)到原點的距離的平方,即|A O|2=13;最小值為原點到直線2x+y-2=0的距離的平方,解得值為。故選C。
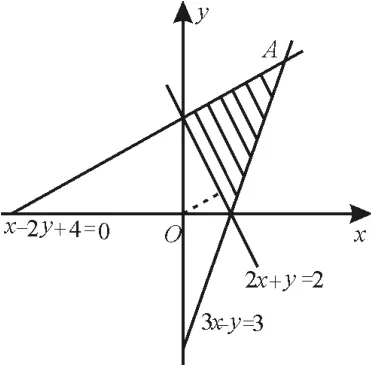
圖3
點評:解決非線性目標函數的最值問題,關鍵是先準確確定目標函數的幾何意義,如表示點(x,y)與定點(a,b)的距離,表示點(x,y)與定點(a,b)連線的斜率,然后根據圖形求最值。
變式訓練2:已知則的 取值范圍是( )。
C.(-∞,3]∪[6,+∞)
D.[3,6]
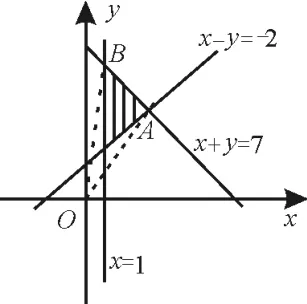
圖4
解:目標函數=表示點O(0,0)與可行域內的點P(x,y)連線的斜率。如圖4,畫出可行域。由得
A;由得B(1,6)。當直線O P過點A時,取得最小值為;當直線O P過點B(1,6)時,取得最大值為6。故選A。
三、已知線性約束條件為參數形式,求線性目標函數的最值問題
例3在約束條件下,當3≤s≤5時,目標函數z=3x+2y的最大值的變化范圍是( )。
A.[6,15] B.[7,15]
C.[6,8] D.[7,8]
解:根據約束條件可畫出可行域,如圖5所示。

圖5
目標函數z=3x+2y,即y=-,可知當斜率為的直線在y軸上截距最大時,z取得最大值。當s=3時,可知當函數經過C(1,2)時,z取到最大值7;而當s=5時,可知當函數經過B(0,4)時,z取到最大值8。所以z的最大值的變化范圍為[7,8]。故選D。
點評:本題考查利用可行域求目標函數的最值,解決此類問題的一般步驟是:(1)作出可行域;(2)找到目標函數取最優(yōu)解時的對應點;(3)將最優(yōu)解的坐標代入目標函數即可求出最值。
變式訓練3:若x、y滿足且z=y-x的最小值為-4,則k的值為( )。
解:z=y-x表示在y軸上截距為z且平行于y=x的直線,z取得最小值-4時,得到直線y=x-4。畫出直線x+y-2=0和y=x-4,由題意知,直線z=y-x經過原不等式所表示的平面區(qū)域的右端點(4,0),從而可知原不等式表示的平面區(qū)域如圖6陰影部分所示。所以直線k x-y+2=0表示在x軸上的截距為4,在y軸上的截距為2的直線,當y=0時,x==4,k=,故選D。
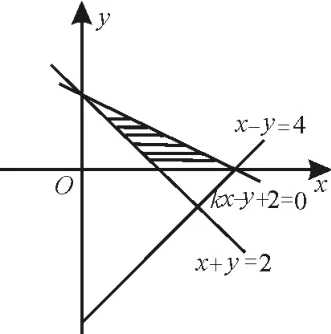
圖6
四、已知最優(yōu)解成立條件,求線性目標函數參數的范圍問題
例4已知變量x、y滿足約束條件若目標函數(z=a x+ya>0)僅在點(3,1)處取得最大值,則a的取值范圍為
解:如圖7,在坐標系中畫出可行域。四邊形A B C D,其中A(3,1),kA D=1,kA B=-1,目標函數z=a x+y(其中a>0)中的z表示斜率為-a的直線系中的截距的大小。若僅在點(3,1)處取得最大值,則斜率應小于kA B=-1,即-a<-1。
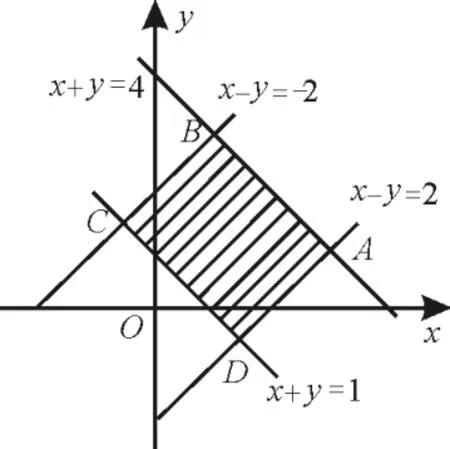
圖7
所以a的取值范圍為(1,+∞)。
點評:用圖解決線性規(guī)劃問題時,若目標函數z=a x+y只在點A處取得最優(yōu)解,則過點A的直線z=a x+y與可行域只有一個交點,由此不難給出直線斜率-a的范圍,進一步給出a的范圍,但在解題時要注意目標函數是取最大值還是最小值,這也是這種題型最容易出錯的地方。
變式訓練4:已知x、y滿足約束條件,使z=x+a y(a>0)取得最小值的最優(yōu)解有無數個,則a的值為( )。
A.-3 B.3 C.-1 D.1
解:如圖8,作出可行域。作直線l:x+a y=0,要使目標函數z=x+a y(a>0)取得最小值的最優(yōu)解有無數個,則將直線向右上方平移后與直線x+y=5重合,故a=1,選D。
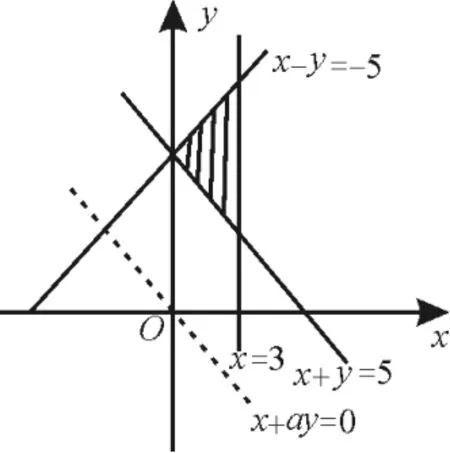
圖8
五、求整數最優(yōu)解問題
例5已知x、y滿足約束條件,求z=7x+5y的最大值。
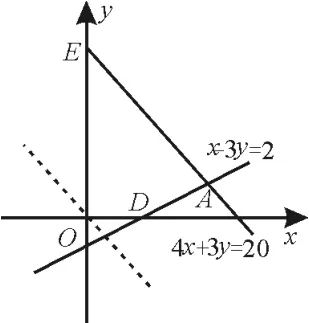
圖9
解:滿足線性約束條件的可行域如圖9中的四邊形A D O E內部的整點及部分邊界整點。通過畫圖發(fā)現(xiàn)直線4x+3y-20=0,x-3y-2=0的交點是理論最優(yōu)解,對應目標函數的理論最大值。但由于A不是整數點,故不是最優(yōu)解。在可行域內所有整點有:(1,1),(1,2),(1,3),(1,4),(1,5),(2,1)(2,3),(2,4),(3,1),(3,2),(4,1),其中可使目標函數值較大的有(1,5),(2,4),(3,2),(4,1)(這些點也是距直線l0:7x+5y=34較近的點),代入目標函數一一驗算,可知當x=2,y=4時,z有最大值34。
點評:如果可行域內整數點是有限的,我們可以寫出可行域內所有整數點,然后再一一代入目標函數,通過驗算,求出整數最優(yōu)解。當可行域內含有無數個整點或整點較多時,這種方法就難以進行了。但可以改進,將接近的整數點逐個代入目標函數,通過驗算,求出整數最優(yōu)解。
變式訓練5:給定區(qū)域令點集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的點},則T中的點共確定條不同的直線。
解:如圖10,陰影部分即為可行域。易得使z=x+y取得最小值的點僅有一個(0,1),使z=x+y取得最大值的點有(0,4),(1,3),(2,2),(3,1),(4,0)。點(0,1)與(0,4),(1,3),(2,2),(3,1),(4,0)中的任何一個點都可以構成一條直線,有5條。又(0,4),(1,3),(2,2),(3,1),(4,0)都在直線x+y=4上,故T中的點共確定6條不同的直線。
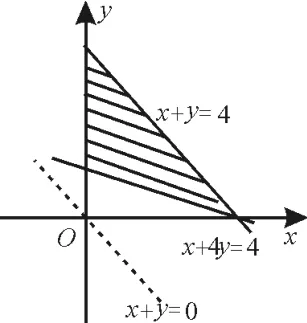
圖10
六、線性規(guī)劃的實際應用問題
例6A,B兩種規(guī)格的產品需要在甲、乙兩臺機器上各自加工一道工序才能成為成品。已知A產品需要在甲機器上加工3小時,在乙機器上加工1小時;B產品需要在甲機器上加工1小時,在乙機器上加工3小時。在一個工作日內,甲機器至多只能使用11小時,乙機器至多只能使用9小時。A產品每件利潤300元,B產品每件利潤400元,則這兩臺機器在一個工作日內創(chuàng)造的最大利潤是元。
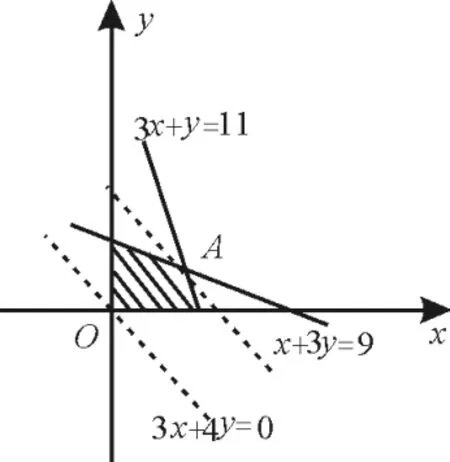
圖11
解:設生產A產品x件,B產品y件,則x、y滿足約束條件生產利潤為z=300x+400y。畫出可行域,如圖11中陰影部分(包含邊界)內的整點,顯然z=300x+400y在點A處取得最大值。由方程組解得=300×3+400×2=1700,故最大利潤是1700元。
點評:解決線性規(guī)劃實際問題的基本方法是:根據題意列出不等式組,畫出可行域,分析目標函數在可行域中取得的最優(yōu)解,最后還原到題目中。

