寬帶LFM信號的壓縮感知測向算法
王雅婧,羅 明
(西安電子科技大學電子工程學院,陜西 西安710071)
0 引 言
寬帶線性調頻(linear frequency modulation,LFM)信號是一種常用的非平穩信號,被廣泛應用于雷達系統中。因此寬帶LFM信號測向問題已成為波達方向(Direction of arrival,DOA)估計的一大熱點。針對多信源環境,經典的寬帶測向算法有非相干子空間處理法 (incoherent signal-subspace method,ISM)[1]和相干信號子空間算法 (coherent signal-subspace method,CSM)[2]。ISM算法原理是將寬帶分解成窄帶,求得各子帶信號的方向估計值,再對其加權得到寬帶信號的測向值;CSM算法將信號變換到頻域后劃分為多個不同頻點的信號,再將其聚焦到特定頻率,應用該頻率的協方差矩陣估計DOA。這兩類算法以及以這兩種算法為基礎的各改進算法[3-5]均是將寬帶轉化為窄帶模型,再利用多重信號分類(multiple signal classification,MUSIC)等方法進行DOA估計。
在窄帶信號DOA估計中,多采用相位法來進行測向,主要利用信號到達測向天線各陣元時產生的相位差估計到達角。陣列接收信號通過鑒相器后得到的相差為[-π,π],當實際的相位差超過這個范圍時,就會出現相位模糊。在接收陣列為均勻圓陣[6-8]時,為了防止出現模糊,限制了圓陣孔徑d<λ/2,在高頻信號環境下滿足無模糊測向的陣列孔徑很小,除了會導致測向精度的降低問題,在工程上也很難實現。
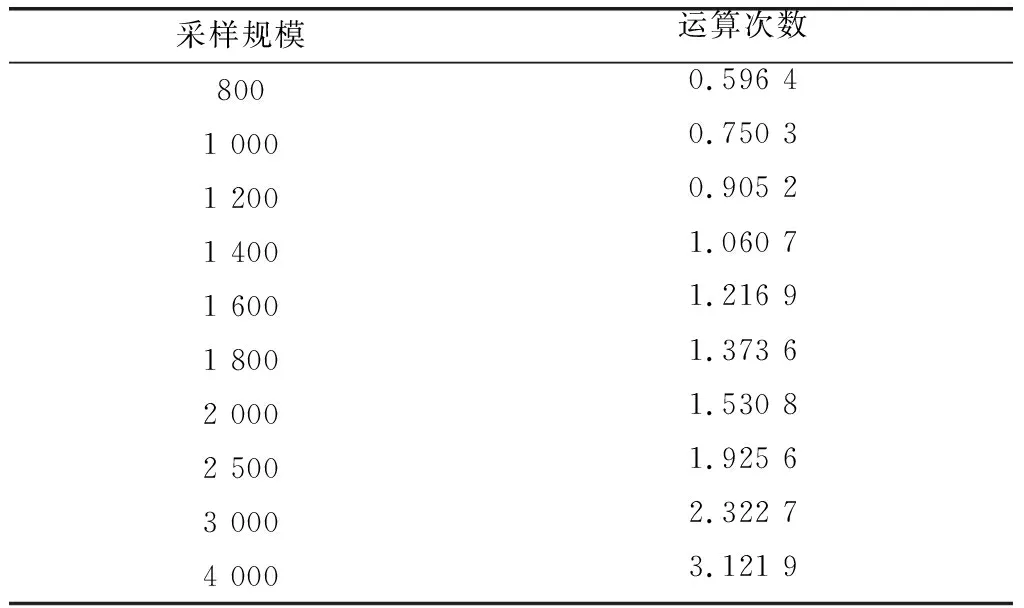
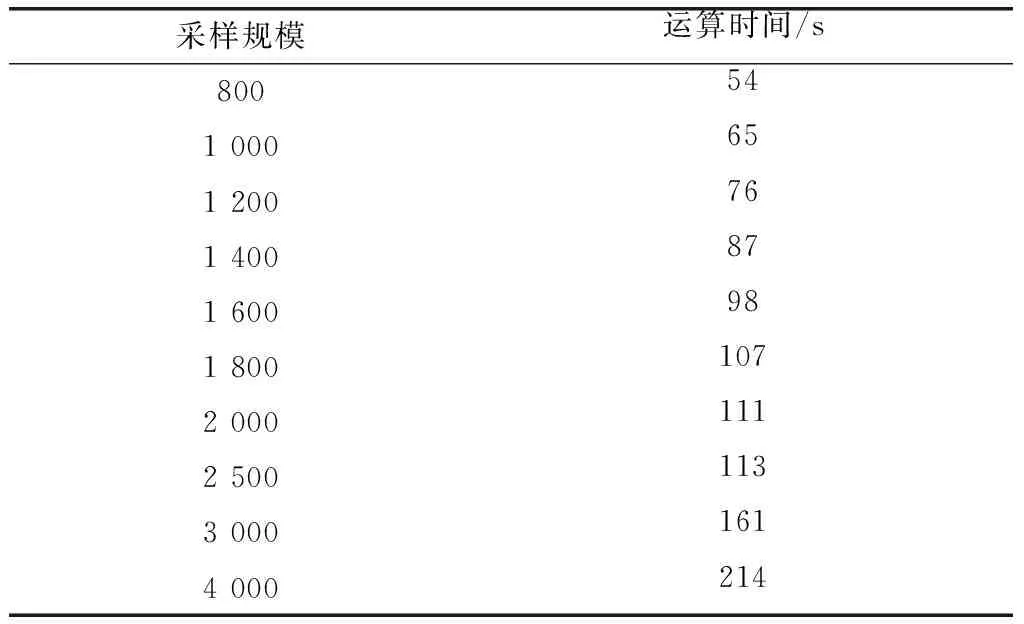
針對這些問題,本文對寬帶LFM信號進行時差法二維測向研究。應用分數時延估計時差法和一維拋物線擬合法的優勢對寬帶LFM信號進行測向,只要滿足時延τ 壓縮感知理論包括3個模塊。 (1)稀疏表示 一個信號矢量Χ∈RN×1,在某個稀疏基Ψ下進行展開為 (1) 其投影系數θi若滿足有K個非零值且K?N,則稱信號X在基Ψ上是稀疏的或者可壓縮的。 (2)降維采樣 采用觀測矩陣ΦM×N實現對信號X的M(K Y=ΦΧ=ΦΨΘ=AΘ (2) 式中,ΦM×N與基字典Ψ不相關;A被稱為測度矩陣、傳感矩陣、CS信息算子。 (3) 信號重構 信號的重構是指由M點采樣的Y測量值恢復長度為N的稀疏信號Θ的過程。為了保證進行有效并且唯一的信號重構,常通過式(3)最優化1范數[10]和貪婪算法求解。 (3) 在壓縮感知框架下,從壓縮信號Y中恢復出稀疏信號Θ,傳感矩陣A必須具有一些特性,即零空間特性、約束等距特性(restricted isometry property,RIP)。 Baraniuk提出了RIP的等價條件:構成傳感矩陣A的測量矩陣Φ和稀疏基Ψ不相關[11]。因此選擇合適的測量矩陣Φ和稀疏基Ψ是確保重構的關鍵。文獻[12]中給出證明,對于一個本身不稀疏,但是關于一個正交基稀疏的信號Χ=ΨΘ,應用測量矩陣Φ得到ΦΧ=ΦΨΘ,運用矩陣Ψ∈RN×N的酉性一旦Φ滿足RIP,則傳感矩陣A=ΦΨ也滿足。測量矩陣Φ常采用Gauss測量矩陣、Bernoulli測量矩陣、部分哈達瑪測量矩陣、部分傅里葉矩陣以及Toeplitz矩陣等,其中Gauss測量矩陣、Bernoulli測量矩陣能夠高概率重構信號,但在實際應用時Toeplitz矩陣物理實現簡單,且壓縮和重構性能同隨機矩陣一樣有效。 本文中采用測量矩陣壓縮信號,并將其觀測向量Y∈RM×1作為接收信號帶入算法進行時差測向。在仿真實驗時采用不同的測量矩陣,將壓縮后的信號帶入分數時延估計算法中,發現只有Toeplitz矩陣作為測量矩陣時,能夠進行準確測向,所以這里只論述Toeplitz矩陣是否滿足RIP特性。 常用的Toeplitz矩陣具有形式為 (4) 文獻[13]中闡明了取Toeplitz矩陣作為測量矩陣ΦM×N時,在滿足M≥C·K3ln(N/K)時矩陣以高概率滿足RIP條件,且跟Toeplitz矩陣相乘可以有效實現快速傅里葉變換,能夠更快實現采集信號和重構信號過程。 本文針對大時寬帶寬的LFM信號為了確保精度必須采用大量采樣數據的問題,主要應用壓縮感知中的降維采樣模塊以減少采樣點數,然后將壓縮后的信號代入時差算法進行測向。所以對于信號的稀疏表示和信號重構這兩大部分,文中只進行了簡要描述,并未進行具體算法研究和仿真驗證。 均勻圓陣具有孔徑小、測向精度均勻、無鏡像模糊、能同時進行方位和俯仰的二維測向等優點,因此文中采用選取五元均勻圓陣作為接收陣列。在圖1建立的xyz坐標系中,圓陣位于xoy平面內,坐標原點為圓心,陣元1位于x軸,其他陣元均勻地分布在圓上。 入射信號在xoy平面上的投影與x軸的夾角記為方位角α,入射信號與z軸夾角為俯角,圖1中所標為仰角β,與俯角互為余角。以原點為參考點,R為圓陣半徑,陣元m的坐標為(Rcos 2π(m-1)/5,Rsin 2π(m-1)/5,0),入射信號的單位向量為(cosβcosα,cosβsinα,sinβ),陣元i到參考點的接收信號時延差為 τi=[(cosβcosα·Rcos 2π(i-1))/5]+ [(cosβsinα·Rsin 2π(i-1)/5)]/v= Rcos(2π(i-1)/5-α)(cosβ)/v (5) 式中,v為電磁波傳播速度,v=3×108m/s。陣元i到陣元j的時延差為 τij=τj-τi=[Rcos(2π(j-1)/5-α)(cosβ)]/c- Rcos(2π(i-1)/5-α)(cosβ)/v= [2Rcosβsin π(j-i)/5sin(α-π(j+i-2)/5)]/v (6) 以一組長基線13、14為例,聯合兩條基線的時差進行測向得 τ13=[2Rcosβsin(2π/5)sin(α-2π/5)]/v (7) τ14=[2Rcosβsin(3π/5)sin(α-3π/5)]/v (8) 對兩條基線時延差分別求和求差 τ13+τ14=[-4Rsin(2π/5)cos(π/10)cosαcosβ]/v (9) τ13-τ14=[4Rsin(2π/5)sin(π/10)sinαcosβ]/v (10) 對式(10)兩邊除以-4Rsin(2π/5)cos(π/10)/v剩余項為cosβcosα,對式(11)兩邊除以4Rsin(2π/5)sin(π/10)/v剩余項為cosβsinα,構造復數 f=cosβcosα+icosβsinα=cosβ·ejα (11) 由式(12)可知cosβ為復數f的模值,方位角α為復數f的輻角,即 (12) 只要已知兩條基線時延差τ13、τ14,即可求得方位角α和仰角β,二維求角問題轉為求時延差問題。 假設接收信號為幅值為1的寬帶LFM信號,表示為 (13) 式中,f0為信號的中心頻率;μ為調頻系數;B為信號頻域帶寬;T為信號脈寬。參考點接收到的信號為 x(t)=s(t)+w(t) (14) 陣元m接收信號為 xm(t)=s(t-τm)+wm(t) (15) 式中,τm為陣元m接收到的信號與參考點接收信號的時間延遲;w(t)和wm(t)為零均值復高斯白噪聲,其方差為σ2,且噪聲間不相關。 為了防止發生頻譜混疊的現象,采樣過程要滿足奈奎斯特定理。針對寬帶LFM信號,傳統采樣得到的離散數據量巨大,加重了運算和存儲的負擔。本文提出應用壓縮感知技術對信號進行降維采樣,將壓縮后的低維信號作為陣元收到的信號進行后續的測向處理。 (16) (17) 文中構建的五元均勻圓陣陣列模型,在不考慮模糊的情況下,在測量精度方面長基線總是優于短基線[17],所以為了獲得高的測量精度,取圓陣中的兩條長基線,聯合進行時差測向。取兩條長基線13、14,對陣元接收信號進行FFT得 (18) 對X1(k)和X3(k)、X1(k)和X4(k)分別進行共軛相乘得 (19) 式中 (20) W1(k)W4(k) (21) 因為LFM信號頻譜抖動不大,所以Y1(k)和Y2(k)可以看作幅度為|S(k)|2,載頻分別為D13=D3-D1和D14=D4-D1的信號,其采樣間隔為1/M,信號的帶寬和原始信號相同,P1(k)和P2(k)為信號的噪聲部分。求解量化時差D13和D14即求解Y1(k)和Y2(k)的信號頻率。 對Y1(k)和Y2(k)進行快速傅里葉變換,對其頻譜圖求譜線峰值位置K1和K2,在[K1-0.5,K1+0.5]和[K2-0.5,K2+0.5]內分別對Y1(k)和Y2(k)進行離散傅里葉變換,得 (22) (23) 式中,c為插值率(c>1),取正整數。在進行求解時c應取合適值,若取太小,則導致估計精度不夠,若取太大,則增加了計算量和運算時間。 (24) (25) 則量化時差D13和D14的精確估計值為 (26) (27) 將兩個長基線時差τ13=D13·Δt和τ14=D14·Δt代入式(10)和式(11),構造復數f對其取模值和輻角即可求得方位角α和仰角β。 通過分數時延估計算法對壓縮后的陣列接收信號進行時差測向,其算法過程與陣列接收信號的時差測向方法相同。但是壓縮感知降低了信號維度,所以大大減少了算法的運算量并且節省了運行時間。壓縮感知測向算法的精度是否與時差測向算法有差異,還需要進一步的仿真研究。 應用壓縮感知之后的分數時延估計算法減少了大量采樣點數,為了評價壓縮感知時差測向算法的優劣,本文對算法各步驟的時間復雜度進行了分析。時間復雜度是算法執行的計算工作量,記作T(n)=O(f(n)),f(n)為算法規模n的函數。兩種區別在于時差估計模塊,所以只分析了時差估計算法的時間復雜度,并跟原分數時延估計算法進行了對比。如表1所示。表1中算法的時間復雜度判定本文中基于壓縮感知的分數時延估計法的優劣,是以N和M的規模來確定的。分數時延估計法在N=10 000(同下文仿真設置)時的運算次數為2.004×108,在M取不同值時的算法的運算次數如表2所示,運算次數的數量級為108。 表1 算法的時間復雜度Table 1 Time complexity of the algorithm 表2 不同規模下基于壓縮感知的分數時延估計算法運算量Table 2 Fractional delay estimation algorithm computation based on compressive sensing at different scales 表2中采樣規模M是在保證能夠正確估計方位角和仰角的前提取值的,由表2可看出當M≤2 500時,基于壓縮感知的分數時延估計測向算法計算量小于原算法,且當M取值越小,計算量越小。評價算法優劣的另一標準是時間效率,即執行算法需要的時間,將在仿真部分進行分析。 假設接收陣列為半徑為R=50 cm的五天線均勻圓陣,入射信號為帶寬B=150 MHz,載波中頻f0=2 GHz,脈寬T=20 μs的寬帶LFM信號,入射方位角α=35°和仰角β=55°。為了保證精度,取采樣快拍數N=10 000,采樣間隔為Δt=T/N=2 ns。取零均值且方差為1的高斯白噪聲為信號噪聲。 實驗1算法的時間效率 表1分析了分數時延估計法和基于壓縮感知的分數時延估計法的時間復雜度,為了直觀表示運算量,進行算法的時間效率即算法運行時間的仿真。仿真實驗的硬件環境為一臺CPU為Intel Core i5-3470(四核3.2 GHz)、安裝內存為4 GB聯想計算機,軟件仿真環境為Matlab R2013b。因為單次實驗的執行時間太短,因此累加500次蒙特卡羅實驗的時間。分數時延估計算法測向的執行時間為115 s,基于壓縮感知采樣的測向算法在M取不同值時的總執行時間如表3所示。 表3 不同規模下算法的運行時間Table 3 Algorithm run time comparison at different scales 表3中算法的運行時間跟表2中的運算次數得到的結論一致,在M≤2 500時,基于壓縮采樣的算法執行時間小于原算法,減少了運算量,節省了測向所用時間。 實驗2不同M下的測向精度 實驗1仿真得到了不同采樣規模M下的壓縮感知測向算法的運行時間,單純從時間效率的角度來看M值越小算法效率越高,但M的取值是否影響測向誤差還需要進一步研究。在信噪比SNR=15 dB環境下,采用分數時延估計時差測向算法和壓縮感知時差測向算法進行了500次蒙特卡羅實驗,以均方根誤差值判定方位角α和仰角β的誤差。仿真結果如圖2和圖3所示。 圖2 不同觀測點下方位角誤差Fig.2 Azimuth error at different observation points 圖3 不同觀測點下仰角誤差Fig.3 Pitch error at different observation points 圖2和圖3中的分數時延估計測向方法的方位角和仰角誤差分別為0.95和1.03,因為在用Matlab進行仿真時構造Toeplitz矩陣的維數過大容易內存溢出,所以仿真設置的采樣點數值不大,并且本文中選取的均勻圓陣為小孔徑,在采樣點數不大的情況下基線越短時差估計的誤差越大,故即使信噪比較大,但測向誤差依舊不會太小。本文旨在對比經過壓縮采樣后的時差測向法和原時差測向法的測向性能,不能單以測向誤差值大小為衡量標準。結合表3在M=1 000時基于壓縮感知的測向模型能夠獲得跟原測向方法相近的DOA估計值,且算法運行時間只需原算法的一半。在M≥1 000時,經過壓縮采樣后的測向算法得到的方位角跟仰角的誤差值跟原算法相近,且隨著采樣點數的增加,測向的誤差值不斷減小。所以應用基于壓縮感知的時差測向算法時,要在確保正確測向的基礎上盡可能選擇較小的觀測值來減少計算量,減輕設備負擔。 實驗3信噪比的影響 權衡算法精度和執行時間,設置壓縮感知的觀測維數為M=1 000。圓陣陣列接收信號的信噪比從11 dB到21 dB以2 dB為步進值增加,進行500次蒙特卡羅實驗,分析并對比了分數時延估計時差測向算法和本文中應用了壓縮采樣后的分數時延估計時差測向算法的測向性能。仿真圖如圖4和圖5所示。 圖4 不同信噪比下方位角誤差Fig.4 Azimuth error at different SNRs 圖5 不同信噪比下仰角誤差Fig.5 Pitch error at different SNRs 如圖4和圖5所示,在信噪比SNR≥15 dB時基于壓縮感知的分數時延估計測向算法得到的測向誤差近似于分數時延估計測向算法。仿真表明,在高信噪比環境下,用壓縮感知的測向模型進行測向,能在不增大測角誤差的前提下,減少大量的采樣點數,減輕軟硬件設備的負擔,減少測向系統所需的運行時間。 本文研究了基于均勻圓陣的寬帶LFM信號測向方法,提出了基于壓縮感知的分數時延估計時差測向方法,解決了采樣點數過大導致的數據冗余和資源浪費的問題,提高了分數時延估計時差測向算法的時間效率。通過仿真實驗得出結論:在高信噪比環境下,壓縮感知時差測向模型的測向性跟分數時延估計時差測向算法相仿,而且在壓縮采樣的觀測點數在滿足一定值(該值遠小于信號采樣點數)時,具有更少的數據計算量和更高的時間效率,大量減少了運算和存儲資源負擔,具有實際研究價值。1 壓縮感知理論
1.1 壓縮感知數學模型
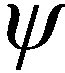
1.2 測量矩陣和稀疏基
2 五陣元均勻圓陣陣列模型
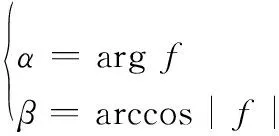
3 基于壓縮感知的寬帶信號時差法測向
3.1 陣列接收寬帶信號的壓縮感知測向模型
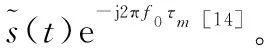
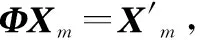
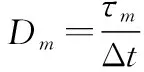
3.2 寬帶信號的分數時延估計法
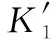
3.3 算法時間復雜度對比

4 仿真實現和分析
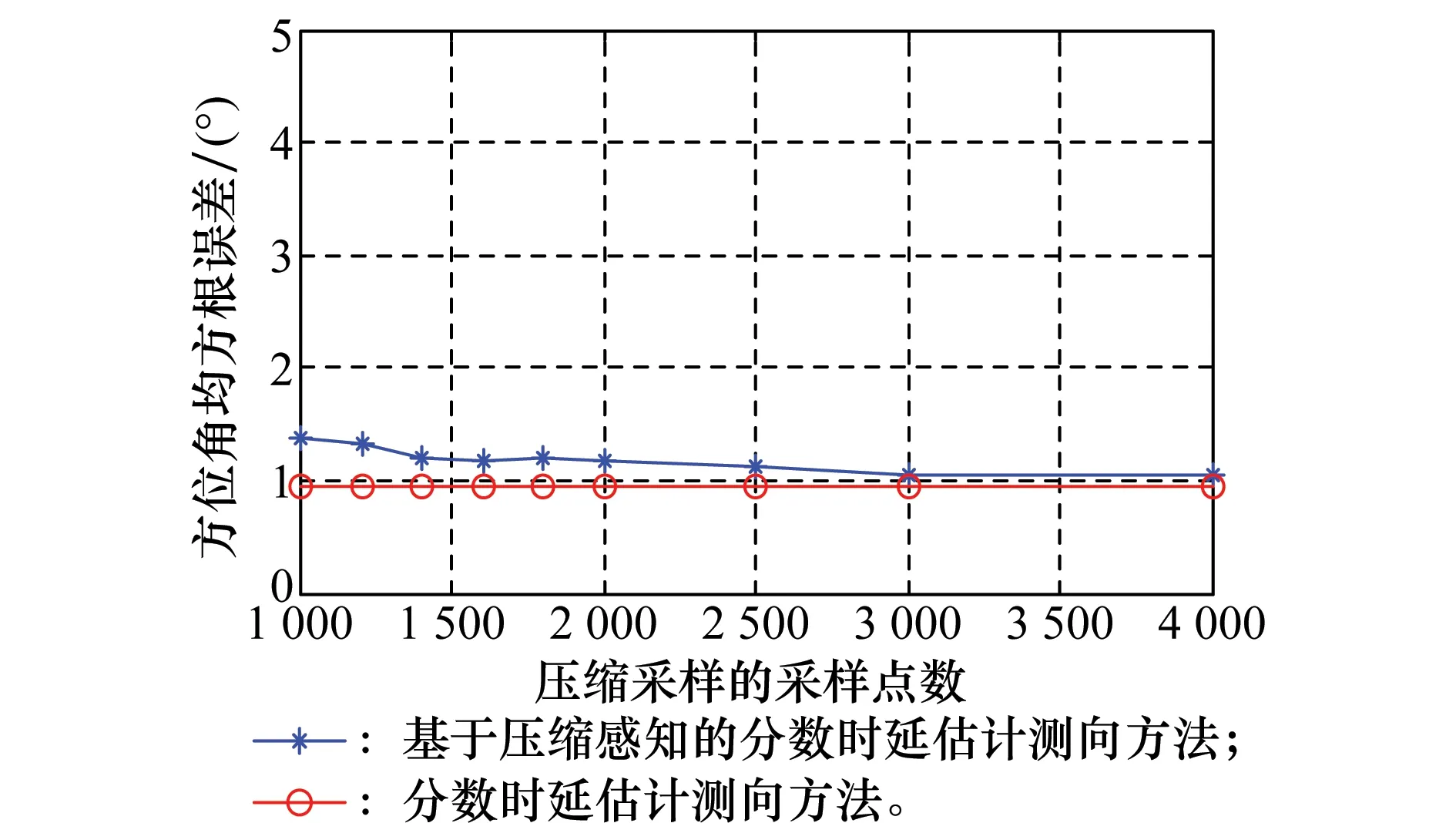
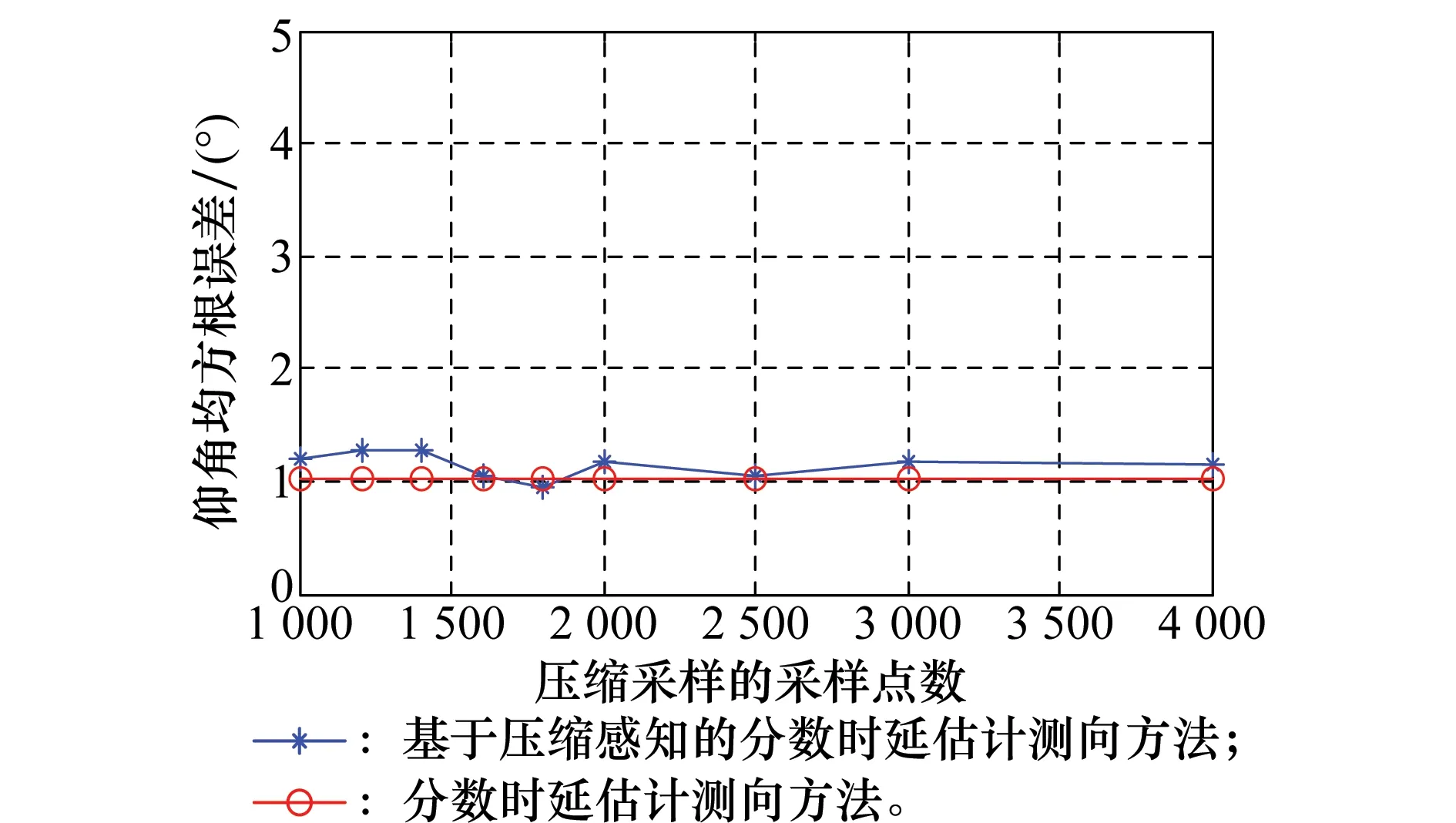
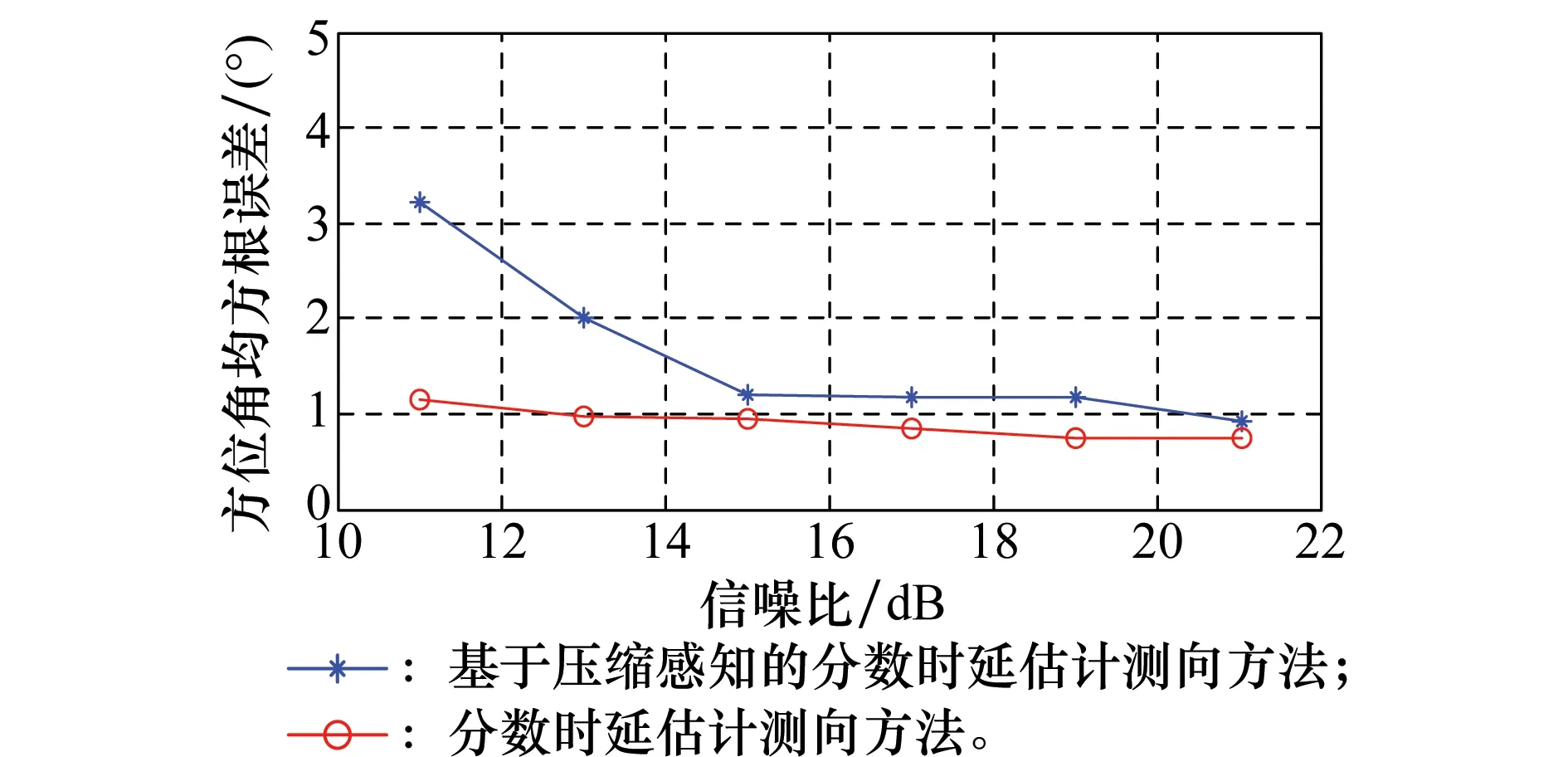

5 結 論

