雷達群目標跟蹤條件下的彈道預報方法
杜廣洋,鄭學合
(1.北京電子工程總體研究所,北京 100854;2.中國航天科工防御技術研究院科技委,北京100854)
0 引 言
在對彈道導彈目標進行跟蹤時,一般情況下,在幾公里的距離波門內聚集著彈頭、誘餌等目標特性不盡相同的分離目標。這些目標大部分有著相近的狀態向量(位置和速度),從而形成近距離物體(closely spaced objects,CSOs)[1-4]。如何對CSOs目標進行穩定、準確地跟蹤和彈道預報,對于目標識別、信息融合等都具有重要意義。
隨著雷達技術的發展,距離高分辨技術越來越多地被采用,對復雜場景下的多目標進行距離分辨和分離目標跟蹤成為可能,即群目標跟蹤[5-8]。在利用群目標跟蹤技術跟蹤CSOs情況下,雷達很難對群內所有目標保持穩定跟蹤。影響因素可能來自于不同的目標散射特性、不同的受干擾程度、航跡交叉等方面[9]。如果群內有子目標跟蹤丟失,則為了維持斷續航跡編號、關鍵事件狀態、多雷達交接等應用需求,需要對丟失目標進行航跡維持[10-12]。常用的方法是利用彈道導彈運動軌跡可預測的特點對丟失目標進行彈道預報。由于目標跟蹤丟失,彈道預報無法獲得觀測數據的修正,因此航跡維持的精度主要取決于目標丟失時刻的初值精度,并且隨著外推時間的增大而變差。
在進行群目標跟蹤時,雷達同時對CSOs中的多個子目標進行同步測量。各個子目標測量信息中的系統誤差、雜波和噪聲干擾、狀態估計的過程噪聲等都具有相同或者相似的性質,即群內多子目標探測信息具有相關性[13]。此時,多子目標之間相對誤差遠小于單個目標絕對誤差。因此,挖掘和利用這一特性,用雷達當前跟蹤的子目標對其他丟失子目標進行相對彈道外推,對于提高航跡維持的精度具有很強的現實意義。
本文提出了利用群內彈道目標的相對運動關系,用雷達正在跟蹤的子目標對其他丟失子目標進行彈道預報的方法。通過誤差分析,對比研究了單純彈道預報與該方法的遞推誤差特性。仿真表明,當雷達對群目標探測信息相關性較好時,該方法大幅提高了彈道預報精度。
1 常用的彈道預報方法及其誤差特性
1.1 單純彈道預報方法
當雷達跟蹤的某個子目標出現跟蹤丟失時,一種最常用的航跡維持方法就是利用以該子目標跟蹤丟失前某個穩定的跟蹤狀態為初值,利用彈道運動方程進行外推。
(1)
式中
μ=3.986 004 418×1014(m3/s2)為地球引力常數;ω=7.292 115 14×10-5(rad/s)為地球自轉角速度。
如果目標跟蹤丟失,并且需要利用彈道預報進行航跡維持,則用四階四級龍格-庫塔法對彈道微分方程式(1)進行數值計算,可以獲得足夠的遞推解算精度[16]。設目標在t時刻運動狀態為St,則在t+1時刻(時間間隔為Δt),運動狀態St+1可進行遞推解算為
(2)
1.2 單純彈道預報方法的誤差分析
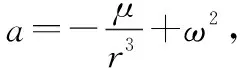
(3)
式中,
St+1≈BSt
(4)
設在k時刻前,雷達跟蹤正常,利用持續的觀測量Z1,Z2,…,Zk可得在k時刻Sk的最小均方誤差估計的協方差矩陣為Pk。若k+1時刻目標跟蹤丟失,則其利用式(1)進行外推的預報狀態協方差陣Pk+1可表示為(忽略過程噪聲)
Pk+1=BPkBT
(5)
若其以Sk為初值利用單純彈道預報方法進行彈道預報,則遞推n步以后狀態量為
Sn=BnSk
(6)
則遞推n步后的預報狀態協方差陣Pn可表示為
Pn=BnPk(BT)n
(7)
由式(7)可見,遞推誤差以跟蹤丟失前狀態估計誤差Pk為起始呈現逐步放大趨勢。
2 群目標跟蹤條件下的相對彈道預報方法
在雷達對CSOs中多個彈道目標進行群目標跟蹤時,由于具有相似的量測偏移量和過程噪聲,群內多子目標間的相對運動狀態估計誤差要明顯優于單個目標的運動狀態估計誤差。因此,當群內某一子目標跟蹤丟失時,若需要利用彈道預報進行航跡維持,可以考慮獲取丟失前群內多子目標間的高精度相對運動狀態,利用未丟失的其他子目標跟蹤航跡用相對彈道預報的方式來維持已丟失子目標的航跡。
2.1 兩個彈道目標相對運動模型
設群內兩個彈道目標的狀態量分別為S1、S2,定義相對運動狀態量為ΔS=S2-S1。則在t時刻,相對運動狀態ΔSt可表示為
(8)
在兩個子目標跟蹤存續期,各個子目標建立獨立的濾波器維護各自的狀態估計值。濾波器可以選取擴展卡爾曼濾波、不敏卡爾曼濾波、多模型等方法[17-20],本文不再贅述。利用式(8)維護一個開環的相對運動狀態估計,以備某一子目標跟蹤丟失后作為彈道預報的初始值。
2.2 目標跟蹤丟失后的航跡維持方法

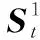
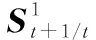

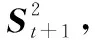
(9)
圖1為子目標2跟蹤丟失前的t時刻和子目標2跟蹤丟失的t+1時刻兩幀的跟蹤狀態估計過程流程圖。

圖1 目標跟蹤丟失前后的狀態估計過程Fig.1 State estimation process before and after target tracking loss
2.3 群目標跟蹤條件下的相對彈道預報方法誤差分析
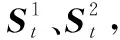
(10)
定義B′=B2-B1,則
(11)

(12)
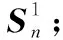

(13)
則遞推n步以后子目標2的預報狀態協方差陣可表示為
(14)
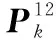
2.4 利用群內目標間的相對運動關系提高彈道預報精度的機理分析
為描述方便,將常用的單純彈道預報方法簡稱為BF-single方法,將本文提出的群目標跟蹤條件下的相對彈道預報方法簡稱為BF-relative方法。
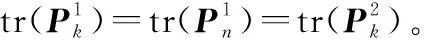
2.4.1 定性分析
假設目標2在k+1時刻以后跟蹤丟失,將式(7)與式(14)做差,可得
(15)
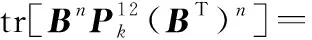
(16)
2.4.2 定量分析
以對高度為500 km的彈道導彈進行彈道預報為例,設雷達對單目標的絕對測量誤差為δS0=[200 200 200 20 20 20],相對測量誤差δΔS0分別為絕對測量誤差δS0的10%、30%、50%和80%幾種情況時(即κ分別為0.1、0.3、0.5、0.8),兩種預報方法的外推時長與位置預報誤差對比如圖2所示。
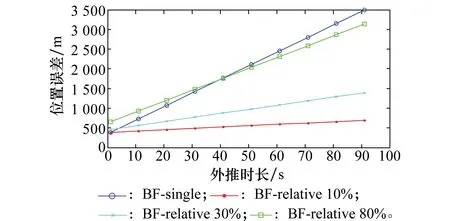
圖2 兩種預報方法的外推誤差對比Fig.2 Comparison of position error between two trajectory prediction methods
由圖2可見,兩種預報方法的誤差大小主要取決于初值時刻絕對誤差或相對誤差的大小,即相對誤差越小則外推誤差越小。這恰恰證明了本文討論問題出發點的正確性。
2.5 群內多個目標時的航跡維持方法
下面將BF-relative方法推廣至更一般的群內多個目標情形。
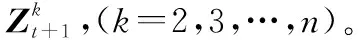
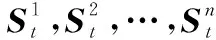
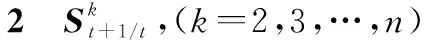
步驟3計算t+1時刻各跟蹤目標對丟失目標1的相對運動狀態預測值和誤差協方差,即
(17)
(18)
步驟4計算t+1時刻各跟蹤目標對子目標1的狀態估計(即預報值)和誤差協方差,即
(19)
(20)
步驟5合成各跟蹤目標對子目標1的狀態估計,計算t+1時刻子目標1的狀態估計和誤差協方差[21-22],即
(21)
(22)
對于群內多個子目標跟蹤丟失的情形,仍可用上述方法,利用剩余跟蹤的航跡維持所有丟失子目標航跡。只要群內還剩余不少于1個子目標跟蹤航跡,就能完成對群內所有丟失子目標的預報航跡更新。
3 仿真分析
3.1 仿真條件
(1)兩個彈道目標情形
利用典型600 km射程彈道導彈彈頭及其分離物的理論彈道,構成由兩個彈道目標組成的CSOs。雷達對這兩個目標進行群目標跟蹤,形成了子目標1和子目標2。前80 s,雷達同時跟蹤子目標1和子目標2;80~220 s,雷達丟失子目標2,只跟蹤子目標1,在下面3種情況下利用彈道預報生成了子目標2的預報航跡。這3種情況包括:①用BF-single方法,以子目標2在80 s丟失前的狀態量為初值進行彈道預報;②用BF-relative方法,用子目標1當前跟蹤航跡,通過相對彈道預報維持子目標2航跡,其中,雷達相對誤差設定為0.01°;③仍用BF-relative方法,雷達相對誤差放大到0.03°。通過仿真檢驗本文闡述的相對彈道預報方法的有效性。仿真參數如表1所示。

表1 仿真參數Table 1 Simulation parameters
(2)多個彈道目標情形
仍利用典型600 km射程彈道導彈彈頭及其分離物的理論彈道,構成由4個彈道目標組成的CSOs。雷達對這4個目標進行群目標跟蹤,形成了子目標1~子目標4。前80 s,雷達同時跟蹤子目標1~子目標4;80~220 s,雷達丟失子目標1,子目標2~子目標4仍能保持跟蹤,在下面兩種情況下利用BF-relative方法生成了子目標1的預報航跡。①只用子目標2當前跟蹤航跡,通過相對彈道預報維持子目標1航跡;②綜合利用子目標2~子目標4當前跟蹤航跡,通過相對彈道預報維持子目標1航跡。通過仿真比較檢驗多個子目標共同維持丟失子目標航跡的精度提升效果。仿真參數與表1一致(其中,雷達相對誤差均設定為0.03°)。
3.2 仿真結果分析
通過跟蹤航跡位置的均方根誤差(root mean square error,RMSE)表征航跡跟蹤或預報效果。假設蒙特卡羅試驗次數為M,則位置的RMSE可表示為
(1) 兩個彈道目標仿真結果分析
作為對比,同時給出以下4種情況位置誤差隨時間的變化曲線:
①子目標1在0~220 s跟蹤位置誤差;
②子目標2在0~80 s跟蹤位置誤差和80~220 s用BF-single方法預報外推的位置誤差;
③子目標2在0~80 s跟蹤位置誤差和80~220 s用BF-relative方法預報外推的位置誤差(01號參數:雷達相對角誤差0.01°);
④子目標2在0~80 s跟蹤位置誤差和80~220 s用BF-relative方法預報外推的位置誤差(02號參數:雷達相對角誤差0.03°)。
仿真結果如圖3所示。
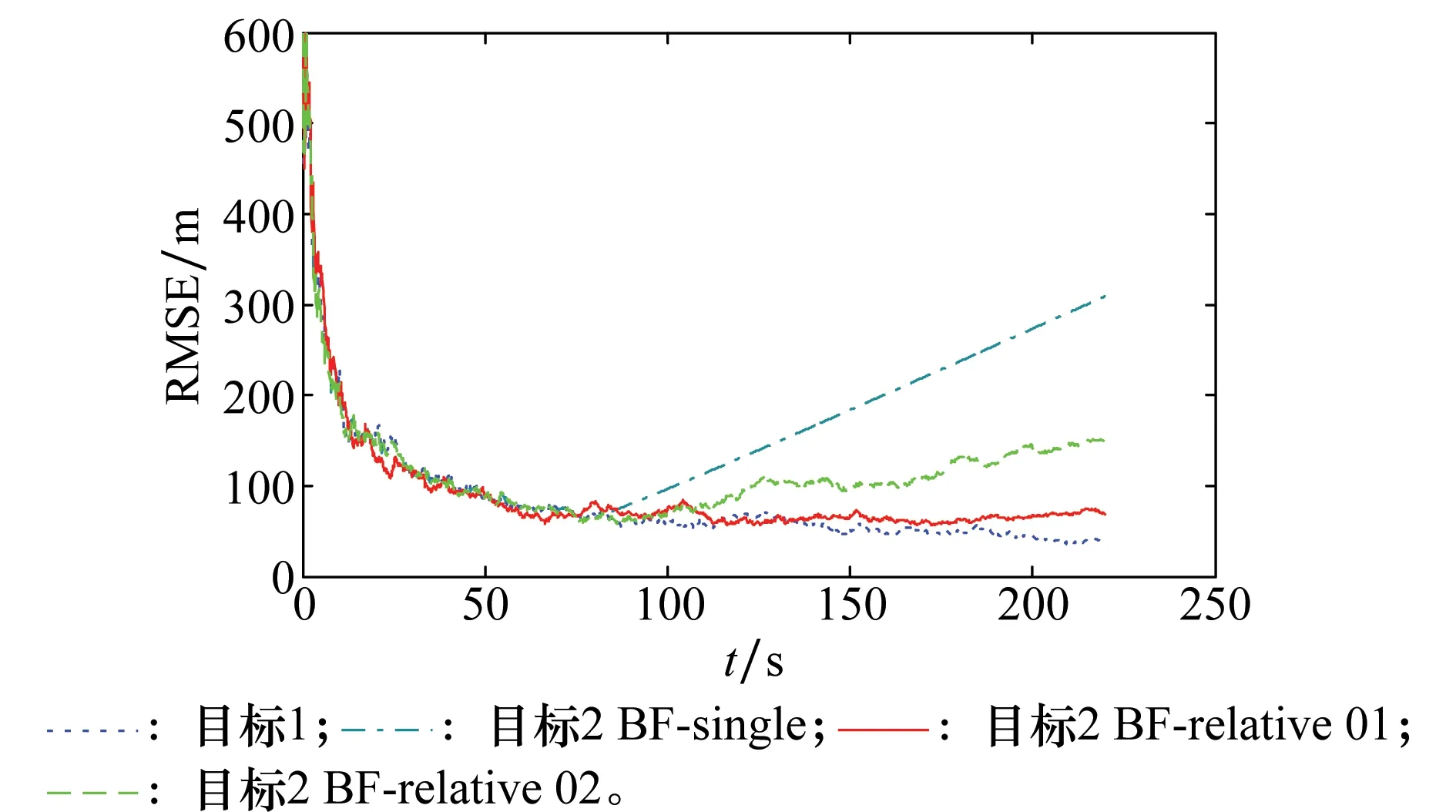
圖3 4種跟蹤位置誤差仿真對比結果Fig.3 Simulation results of tracking position error in four cases
仿真結果與誤差特性分析的結論是一致的,即當雷達對多目標探測信息相關性較好時,相比于BF-single方法,本文提出的BF-relative方法大幅提高了彈道預報精度。當雷達相對誤差較小時(在上述仿真場景下為0.01°,即相對測量誤差為絕對測量誤差的10%),BF-relative方法得到的目標2預報航跡與目標1的跟蹤航跡位置誤差基本相當。
(2) 多個彈道目標仿真結果分析
作為對比,同時給出以下兩種情況位置誤差隨時間的變化曲線:
①子目標1在0~80 s跟蹤位置誤差和80~220 s用2個彈道目標相對關系預報外推的位置誤差;
②子目標1在0~80 s跟蹤位置誤差和80~220 s用4個彈道目標相對關系綜合預報外推的位置誤差。
仿真結果如圖4所示。仿真結果表明,當群內有超過兩個子目標時,只要群內還剩余不少于1個子目標跟蹤航跡,就能完成對群內所有丟失子目標的預報航跡更新,但相比于利用兩個子目標間相對關系維持丟失子目標航跡,用多個子目標共同維持丟失子目標航跡的精度提升效果明顯。因此,在計算資源允許時,應盡量選用多個目標合成外推的方法。
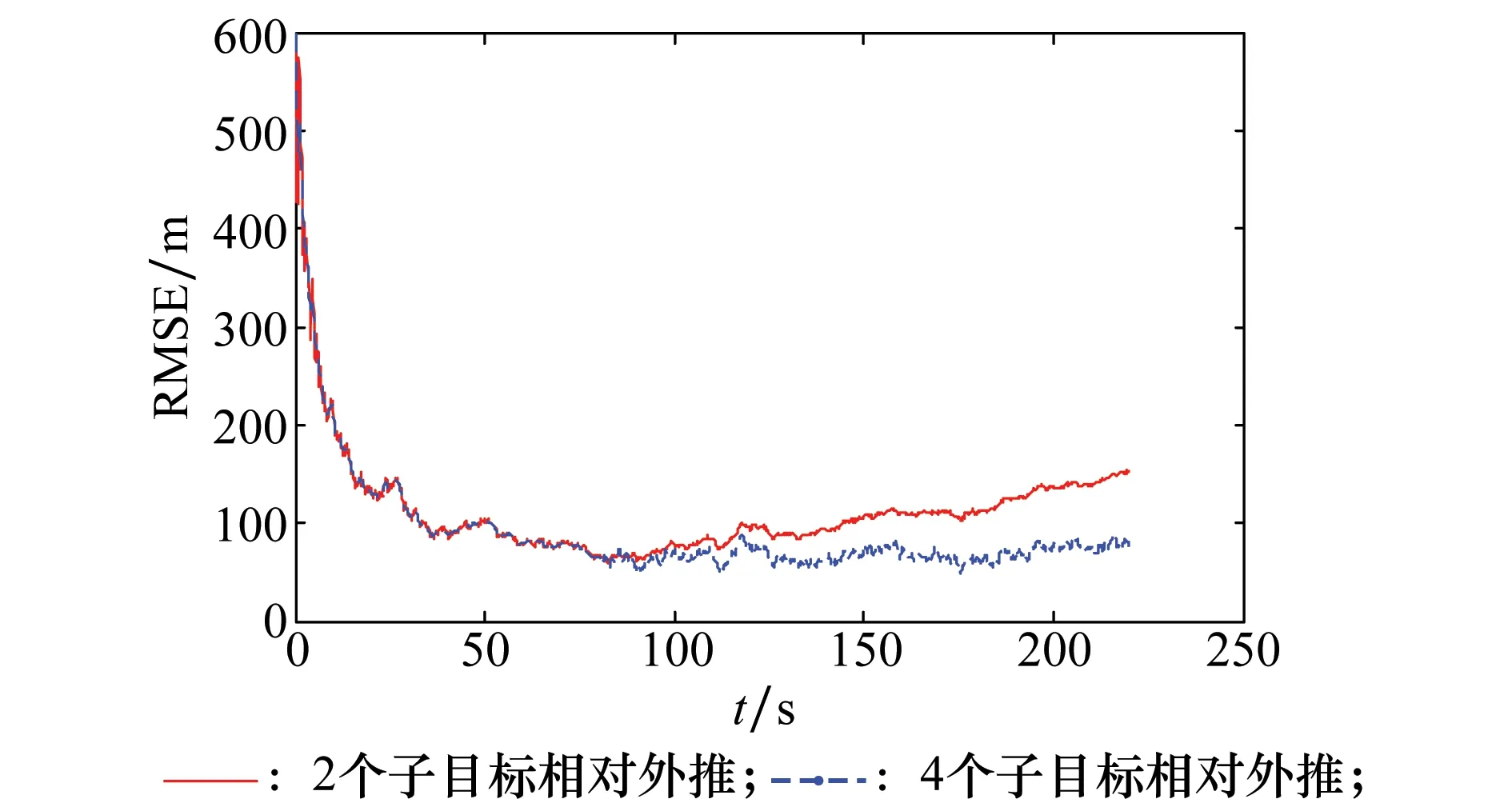
圖4 兩個和4個彈道目標預報位置誤差仿真對比結果Fig.4 Simulation results of tracking position error in two and four tracks
4 結 論
提出了空間群目標跟蹤條件下的BF-relative方法。本方法挖掘利用了雷達在探測群目標時相對誤差一般小于單個目標的絕對誤差的特性,通過仿真表明,本方法相比傳統單目標BF-relative方法精度大幅提高。
需要說明的是,該方法的基礎是該預測的相對誤差能較好地作為估計狀態相對誤差的估計,而這需要有一定前提的,即群目標間不能發生機動運動,一旦其中一個目標存在機動運動,這個相對誤差估計結果就是錯誤的。
通過誤差分析,探討了本方法誤差傳遞機理,同時,也明確了后續進一步提升彈道預報精度的方向。今后的工作是研究進一步提升跟蹤存續期群目標間相對精度的實時狀態估計方法。

