牛頓型黏性物料轉盤離心霧化成粒特性

王東祥崔政偉俞建峰楊新俊

WANG Dong-xiang1，2 CUI Zheng-wei1，2 YU Jian-feng1，2 YANG Xin-jun1，2

(1. 江南大學機械工程學院，江蘇 無錫 214122；2. 江蘇省食品先進制造裝備技術重點實驗室，江蘇 無錫 214122)

(1. College of Mechanical Engineering, Jiangnan University, Wuxi, Jiangsu 214122, China; 2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment & Technology, Wuxi, Jiangsu 214122, China)

離心霧化利用機械旋轉形成離心力將物料液流破碎為液滴，進入氣相冷卻凝固，可顯著改善氣—液或氣—固相間的接觸與混合，強化熱質傳遞，縮短操作時間，廣泛應用于食品和材料行業熱敏性物料的粉體制備[1]及快速干燥[2-3]等領域。相比其它離心粒化器，普通轉盤完全能達到相同霧化效果，且慣性力更低、節能、穩定性更高，應用相對廣泛[4-5]。當澆注至轉盤時，物料因離心作用向外延伸并在轉盤表面沿徑向形成連續分布的液膜，液膜運動至轉盤邊緣失穩破碎并最終形成液滴，其成粒特性是決定霧化顆粒尺寸、形態并進而作用于其冷卻速率與最終產物品質的關鍵因素[6-7]。

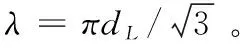
本試驗擬以轉盤離心霧化器為研究對象，松香-石蠟混合物為原料，結合試驗研究與數值分析，針對不同霧化工藝參數的成粒特性開展研究，分析纖維數量、直徑，界面波波長和顆粒粒徑的作用機理，實現纖維直徑、界面波波長和顆粒粒徑的準確預測，進一步揭示成粒特性的演變規律，為轉盤離心霧化系統設計與優化提供可借鑒的理論與應用基礎。

1 材料與方法

1.1 材料

為便于粒徑分析，所選物料在常溫下應可凝固，綜合考慮后，選擇松香—石蠟混合物作為試驗介質，控制松香和石蠟質量比為4∶1，表1為所選物料物性參數。

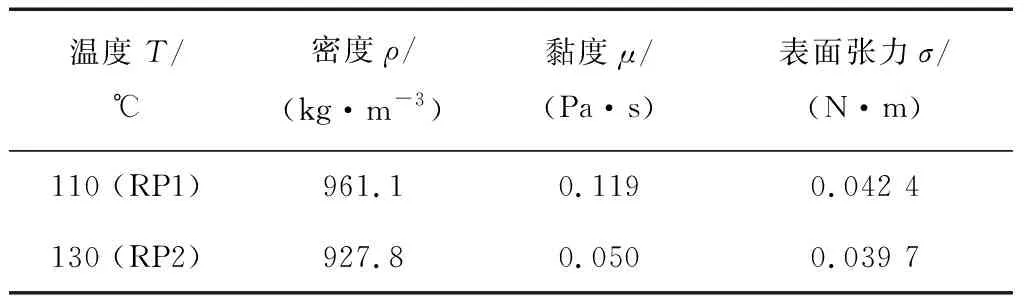
表1 松香—石蠟混合物物性參數

1.2 儀器與設備

超聲流量計：FLEXIM G601型，英國帕爾希森有限公司；

高速攝像儀：Phantom Miro R320S型，美國Vision Research公司；

電子天平：C-144型，上海友聲衡器有限公司。

1.3 方法

1.3.1 試驗方法 給定轉盤結構和物料，調整轉速ω與介質流量Q開展試驗，如圖1所示，試驗物料由澆注管流至轉盤軸心，管口距轉盤上表面10 mm。轉盤材料304不銹鋼，直徑D分別為50，100 mm，表面拋光，粗糙度Ra=1.60 μm。試驗物料流量0～25 mL/s，轉速62.8～188.5 rad/s。按質量比4∶1配置松香—石蠟混合物，以填滿坩堝為宜，試驗物料由電磁加熱熔化至指定溫度，經控制閥調節流量后澆注。單次試驗完畢，收集樣品，稱重，以標準篩網篩分，以顆粒平均直徑dm、顆粒尺寸分布作為衡量指標評價成粒效果，顆粒平均直徑可按式(1)計算：

(1)

式中：

dm——顆粒平均直徑，mm；

di——某規格篩網篩分所得顆粒的平均尺寸，mm；

ζi——某規格篩網篩分所得顆粒的質量分數，%。

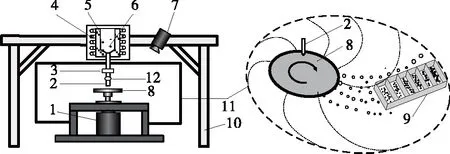
1. 電機 2. 澆注管 3. 閥門 4. 電磁加熱器 5. 坩堝 6. 松香—石蠟 7. 高速攝像儀 8. 轉盤 9. 樣品收集 10. 支座 11. 粒化室 12. 流量計

圖1 試驗裝置

Figure 1 Schematic diagram of experimental apparatus

1.3.2 顆粒粒徑預測模型 相比滴狀與膜狀，完全纖維狀成粒是最理想的霧化模式，本試驗均在該模式下進行。圖2所示為轉盤離心霧化纖維狀成粒原理，包含轉盤表面薄膜流形成、薄膜流纖維化以及纖維斷裂形成液滴3個過程。

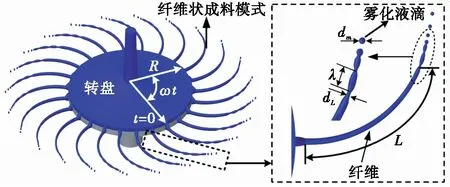
圖2 轉盤離心霧化成粒原理

隨著纖維向外延伸，纖維逐漸變細并因表面張力作用發生頸縮而斷裂。對于給定轉速，完全纖維狀成粒時，纖維數量不隨物料體積流量變化而為一定值，顆粒尺寸dm則可通過頸縮斷裂時的界面波波長λ與纖維直徑dL來估計[10]。若假設單個波長內的纖維直徑為常量，且忽略斷裂時形成的少量衛星液滴的影響，顆粒平均粒徑dm可以通過式(2)計算：

(2)

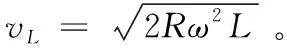
(3)

式中：

C——待定常數；

KL——纖維數量，可以通過We和St表征。

若定義無量綱體積流量QR=ρQ2/σR3，則式(3)可進一步簡化為：

(4)

式中：

We——韋伯數，We=ρω2R3/σ；

St——穩定數，St=μ2/ρRσ；

R——轉盤半徑，m；

Q——物料流量，mL/s；

ρ——物料密度，kg/m3；

μ——物料運動黏度，Pa·s；

σ——表面張力，N·m。

結合式(2)、(4)，顆粒平均粒徑dm的預測模型為：

(5)

纖維斷裂時的界面波波長λ與纖維直徑dL很難通過試驗測量，且理論上難以計算，本研究擬通過計算流體動力學分析求得，結合試驗獲得的纖維數量KL與統計分析獲得的顆粒平均粒徑dm，即可建立顆粒尺寸預測模型。

1.3.3 數值方法 VOF方法可以表征復雜相界面的結構與演變，相界面銳利程度較高。相比其它相界面追蹤方法，在描述復雜相界面和處理三維相界面的融合與破碎問題時具有潛在的優勢，本試驗將采用FLUENT.15.0平臺集成的VOF模型表征轉盤邊緣液膜的纖維化特性，獲得纖維斷裂時的界面波波長λ與纖維直徑dL等參數。做如下假設：① 物料相流量恒定，呈連續、均勻流動，轉盤附近的空氣相流動行為僅受轉盤以及物料影響；② 轉盤表面液膜的流動行為可假設為旋轉周期性流動；③ 計算區域僅包括轉盤邊緣以及附近空氣相區域；④ 物料在轉盤表面溫度變化非常小，忽略物料與轉盤之間的熱量傳遞。圖3、4為簡化的三維物理模型、邊界條件示意圖以及網格劃分圖。轉盤表面液膜的流動特性作為邊界條件加入計算模型，包括液膜厚度、徑向速度以及切向速度滑移，可根據筆者前期研究[7]計算。模型周向僅包括弧度為θ的區域，θ角的選取應保證計算區域內至少形成2根纖維，需通過大量計算嘗試以最終確定θ值范圍。

模型進口采用速度入口邊界(Velocity inlet)，物料體積分數為1，給定入口處物料徑向速度以及切向速度滑移量。出口區域流體充分發展，設定為自由出口(Pressure outlet)，2個周向界面為旋轉周期性邊界(Periodicity)，轉盤表面以及側面為無滑移邊界條件。

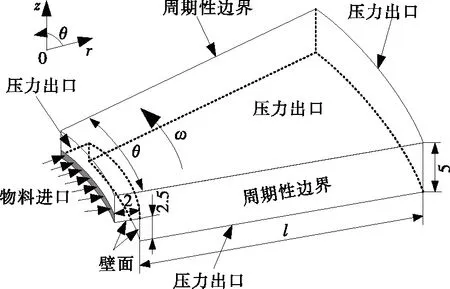
圖3 數值模型與邊界條件示意圖

圖4 模型網格局部放大圖

2 結果與分析

2.1 成粒模式

由圖5(a)可知，當Q=1.28 mL/s時，液膜在轉盤邊緣直接破碎形成液滴并凝固，呈滴狀成粒模式，顆粒形態和尺寸相對均勻。當Q增至7.68 mL/s時，滴狀過渡至完全纖維狀成粒模式，液滴均因纖維緊縮斷裂而成[圖5(b)]，纖維數量達到最多且不隨流量改變，成粒過程趨于準穩定，顆粒較為均勻且粒徑分布窄。當Q增至21.84 mL/s時，纖維融合，呈膜狀成粒模式，顆粒主要有2種生成模式，一是由液膜直接破碎而成；二是液膜可一次破碎形成纖維，纖維二次破碎形成顆粒[圖5(c)]。相比滴狀與纖維狀，膜狀成粒時，顆粒形態和尺寸均較為不均勻。對于給定操作條件，應嚴格控制物料流量，確保成粒模式集中于完全纖維狀模式。圖6為纖維狀成粒模式數值模擬與試驗對比圖。雖然數值模擬與試驗轉速方向相反，但在相同操作條件下，數值計算結果與試驗吻合較好，纖維運行軌跡一致，纖維數量分別為46與45，基本一致，根據數值計算結果可以獲得界面波波長、纖維直徑等有效信息。

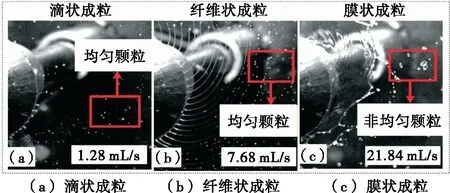
D=50 mm, ω=94.3 rad/s

2.2 纖維數量

圖7為轉盤直徑分別為0.05，0.10 m時，纖維數量與轉盤轉速的關系曲線。對于D=0.05 m的轉盤，隨著轉速由62.8 rad/s 增加至188.5 rad/s，RP1物料的液柱數量由31增加至78，RP2的液柱數量則由37增加至84。對于D=0.10 m的轉盤，RP1物料的液柱數量由82增加至188，RP2的液柱數量則由94增加至206。相同轉盤和轉速條件下，2種物料的纖維數量差別并不是太大，以0.05 m的轉盤以及轉速188.5 rad/s為例，RP2的纖維數量較RP1僅高出7.1%。雖然2種工質的黏度相差很大，但表面張力非常接近(表1)，可以推知，在黏度范圍內(0.050～0.119 Pa·s)，纖維數量主要受表面張力影響，而黏性力的影響則要小得多。因此，在相同轉盤結構與轉速條件時，較低黏度物料轉盤離心霧化的纖維數量可以只考慮表面張力的影響，而黏度的影響可以忽略。如圖8所示，經線性回歸，液柱數量與We以及St的關系可以表示為式(6)，回歸系數R2=0.96，各參數適用范圍分別為We=1.40×103～1.04×105，St=1.38×10-3～1.39×10-2。

KL=0.971We0.438St-0.059。

(6)

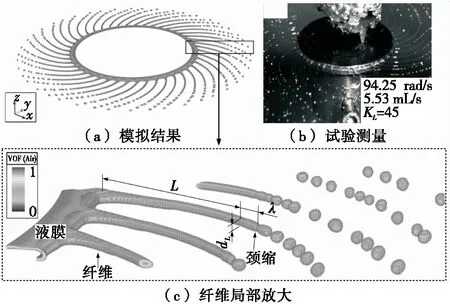
圖6 纖維狀成粒數值模擬與試驗對比

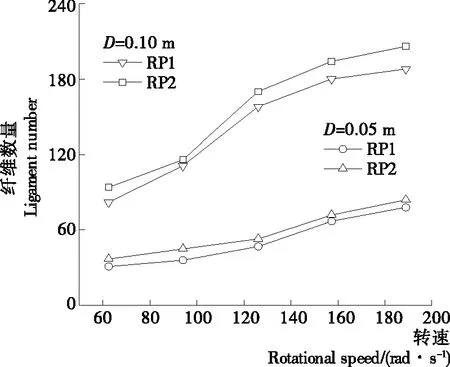
圖7 液柱數量與轉速的關系曲線

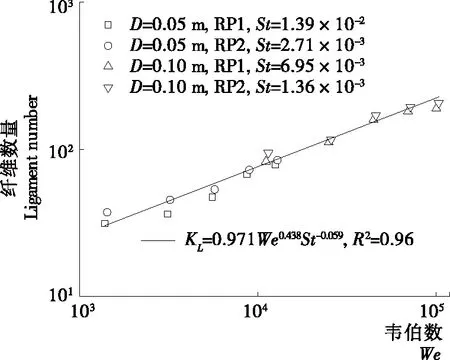
圖8 纖維數量與We的關系曲線

2.3 纖維直徑

由圖9可以看出，轉速的升高顯著降低了纖維直徑，相同轉速條件下，物料黏度較高時，纖維直徑也較大。對于D=0.05 m 的轉盤，當轉速由62.8 rad/s 增加至188.5 rad/s，RP1的纖維直徑由0.619縮小至0.352 mm，RP2則由0.563縮小至0.328 mm，而對于D=0.10 m的轉盤，2種物料的尖端直徑則分別由0.385縮小至0.272 mm以及0.293縮至0.230 mm。在較大轉盤直徑或較高轉速條件下時，轉盤邊緣形成更多纖維，纖維直徑也相應減小。

圖10為轉速125.7 rad/s時液纖維直徑與物料體積流量的關系曲線。纖維直徑隨著物料流量的增加而呈緩慢上升趨勢，并沒有引起纖維直徑顯著增大。對于D=0.05 m的轉盤，隨著流量由4 mL/s增大至7 mL/s，RP1纖維直徑由0.389 mm 升至0.392 mm，RP2也僅由0.352 mm上升至0.354 mm，對于D=0.10 m的轉盤也有同樣結論。完全纖維狀成粒模式時，由于纖維數量維持不變，因此物料流量的增加主要通過纖維長度的延伸來體現，而不會引起纖維直徑顯著改變，但物料物性對于纖維直徑有較大影響。結合式(4)，經線性回歸，纖維直徑dL可通過式(7)預測，回歸系數R2=0.93，各參數適用范圍分別為We=1.40×103～1.04×105，St=1.38×10-3～1.39×10-2。

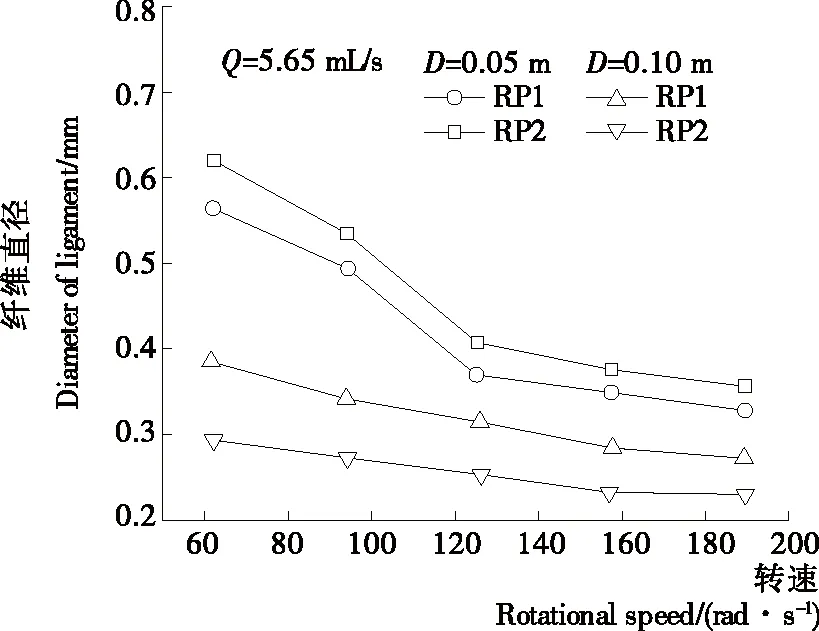
圖9 纖維直徑與轉速的關系曲線

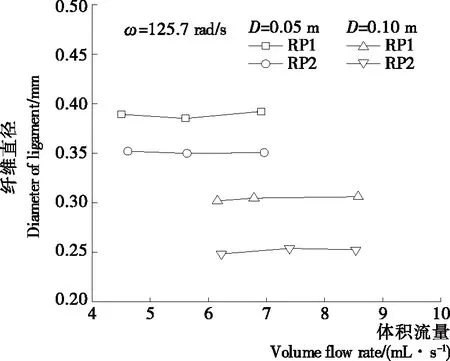
圖10 纖維直徑與流量的關系曲線

(7)

2.4 界面波波長

Weber[16]針對圓管射流的研究表明，纖維的斷裂呈長波模式，界面波波長與纖維直徑間有λ/dL=4.50的關系。而Shinjo等[15]針對微重力條件下的圓管受限射流研究表明λ/dL=1.81，呈短波斷裂模式，如圖11所示，在本研究的操作條件下，界面波波長主要分布在長波與短波之間，呈λ/dL≈3.56的關系。纖維直徑<0.5 mm時，界面波波長向短波模式靠攏，而當纖維直徑>0.8 mm時，趨向于長波斷裂模式。需要指出的是，長波斷裂時，界面波必須通過具體物理實體的反射，由于多普勒頻移的作用而導致界面波波長增大，而在轉盤離心霧化成粒過程中，纖維來源于轉盤邊緣液膜的失穩纖維化而自由形成，無具體物理邊界限制；另外，Shinjo等[15]的研究針對的是微重力條件下的圓管受限射流，而在離心霧化工程中，纖維的斷裂處于離心力場中，纖維在離心作用下將會被拉伸，由此導致其斷裂的界面波波長增大，從這點來考慮的話，纖維的斷裂應該仍是以短波模式為主。

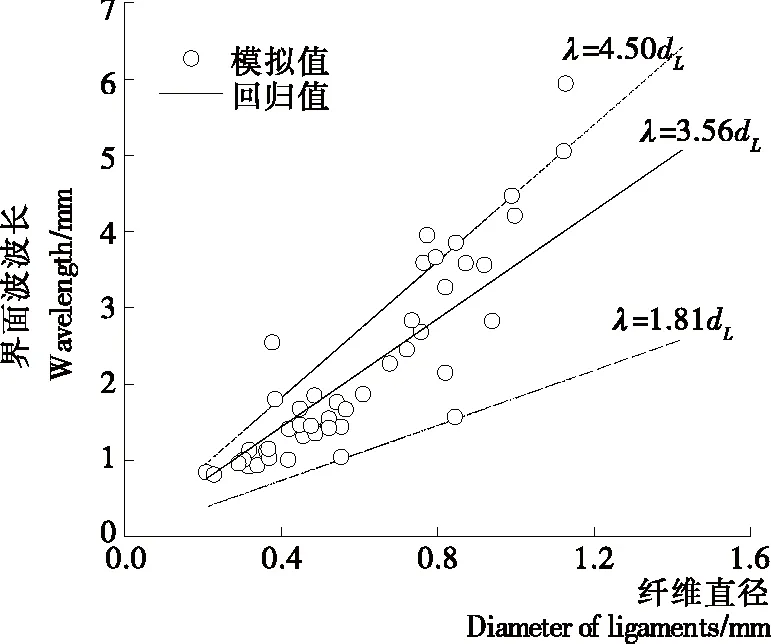
圖11 液柱尖端直徑與界面波波長

2.5 顆粒粒徑

結合纖維直徑dL、界面波波長λ以及式(5)，顆粒平均直徑dm可以通過式(8)進行預測，式中各參數適用范圍分別為We=1.40×103～1.04×105，St=1.38×10-3～1.39×10-2，QR=5.79×103～7.27×104。

(8)

圖12為不同轉速條件下的顆粒粒徑測量值與式(8)預測值對比以及給定操作條件下的顆粒樣品圖。由圖12可知，試驗測量值與預測結果吻合較好。對于相同的轉盤結構和物料體積流量，提高轉速可以縮小顆粒粒徑。隨著轉速從62.8 rad/s增加至188.5 rad/s，對于D=0.05 m的轉盤，RP1獲得的顆粒平均直徑由0.64 mm降至0.51 mm，RP2則由0.45 mm 降至0.39 mm。提高轉速使得轉盤表面的液膜厚度降低，液膜在轉盤邊緣纖維化后形成更多纖維，纖維直徑相對減小，粒徑也因此降低。另外，高轉速條件下因液膜與轉盤間速度滑移顯著增大，顆粒粒徑變化已不明顯，因此不建議無限制增加轉速來控制顆粒粒徑，可以考慮如增大轉盤直徑或者改善轉盤表面拓撲結構等途徑。

如圖13所示，顆粒的平均粒徑隨著物料流量的增加而顯著增大。對于D=0.05 m的轉盤，當流量由4.53 mL/s增加至6.92 mL/s，RP1的顆粒平均粒徑處于0.41～0.74 mm；RP2處于0.39～0.59 mm，對于D=0.10 m的轉盤也可得到類似結論。完全纖維狀成粒模式時，纖維數量已維持不變，物料流量的增加主要通過纖維直徑的加大以及纖維長度的延伸來體現，顆粒粒徑與纖維直徑以及界面波波長直接相關，因此顆粒粒徑隨流量提高而增大。

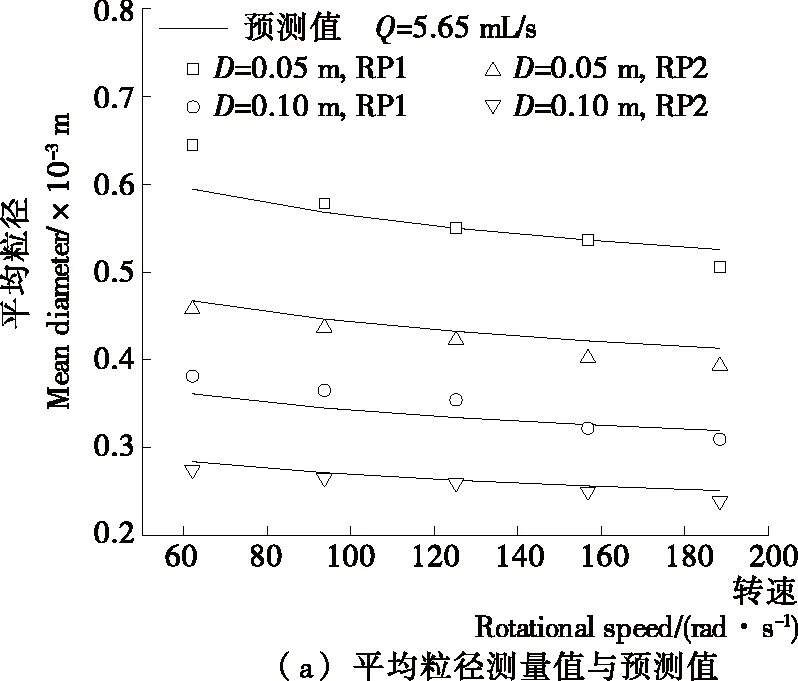
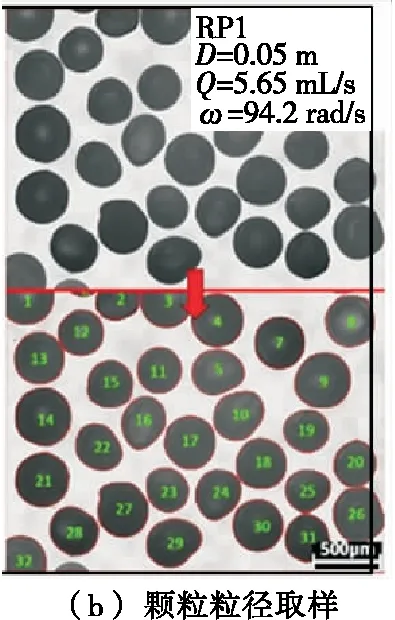
圖12 不同轉速條件下的顆粒平均尺寸測量值與預測值對比

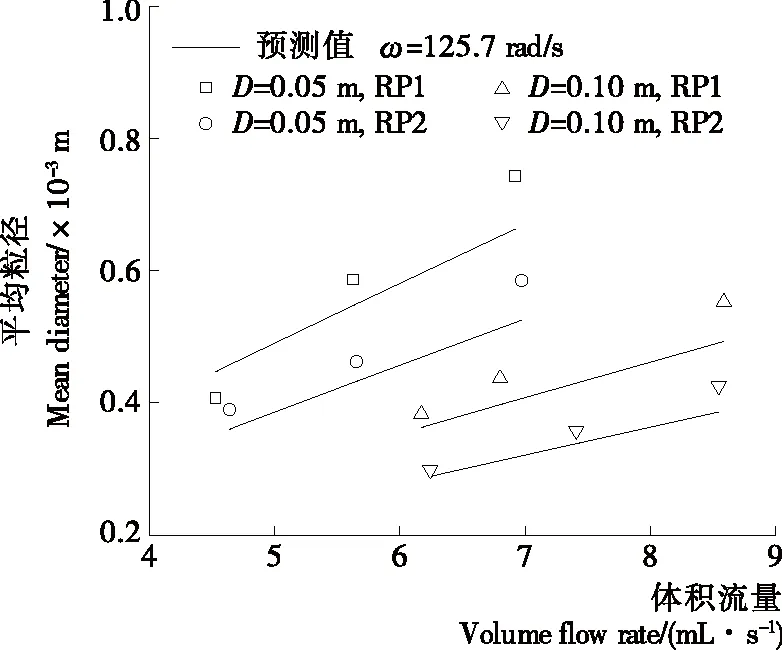
圖13 不同流量條件下的顆粒平均尺寸測量值與預測值對比

3 結論

本研究針對轉盤離心霧化器，采用試驗研究結合數值分析方法，通過理論研究結合量綱分析，研究了松香—石蠟混合物的成粒特性，結論如下：

(1) 黏性液膜在轉盤邊緣破碎形成的纖維數量主要取決于無量綱韋伯數與穩定數，低黏度物料的纖維數量主要受表面張力影響，可忽略黏性力作用。

(2) 針對完全纖維狀成粒模式，獲得了纖維數量、纖維直徑以及顆粒粒徑的無量綱經驗模型，為轉盤離心霧化工藝調控與系統設計提供了支撐。

(3) 纖維緊縮斷裂的界面波波長為纖維直徑的3.56倍，處于Rayleigh長波模式與Shinjo短波模式之間，考慮到纖維所受離心拉伸作用，其斷裂仍然為Shinjo短波模式。

(4) 顆粒粒徑不建議僅通過轉速進行調控，高轉速時的液膜與轉盤間速度滑移增大引起顆粒粒徑已不再明顯減小，可以采用如增大轉盤直徑或者改善轉盤表面拓撲結構等途徑實現。