基于多鏈MCMC方法的光伏出力序列預測研究

樊安潔， 高 山， 方濟城 ， 韓海騰， 吳 晨

(1. 東南大學電氣工程學院,江蘇 南京 210096；2. 上海電力學院電子與信息工程學院， 上海 200090；3. 國網江蘇省電力有限公司經濟技術研究院，江蘇 南京 210008)

0 引言

隨著光伏發電滲透率的提高，光伏出力功率的隨機性對電力系統的規劃和運行提出了更高的要求。研究光伏出力時間序列的生成方法，更好地研究其出力的特性，對于進一步研究滿足電力系統規劃和運行具有重要的意義。電力系統的規劃需要未來長時間的光伏預測出力數據作為分析基礎，因此光伏出力功率預測模型應當能夠從有限的實測數據中充分學習光伏出力的特性，保留歷史出力的基本統計規律，涵蓋影響光伏出力不確定性的各種因素。目前光伏序列的隨機生成算法主要包括神經網絡算法、支持向量機算法、卡爾曼濾波算法、馬爾可夫鏈算法等[1-2]。其中傳統一階馬爾科夫鏈模型在現有的風光發電功率的預測中取得了較好的效果，能夠生成在概率特征及波動特性上與原始序列較為精確的預測序列[4-8]。

目前對光伏出力功率的研究主要集中在對單個光伏電源出力序列的模擬上。未來的電力系統規劃中，為充分計及影響可再生能源出力不確定性的各項因素，在模擬可再生能源出力的時間序列時要考慮它們之間的相關特性[9-10]。文獻[11]采用典型日方法描述無云狀態下的太陽輻照情況，并引入向量自回歸模型，較好模擬了歷史出力中各分解成分的統計特征和各時間尺度下的波動特性，保留了光伏電站之間的相關性。但由于向量自回歸模型的限制，該模型適合于短時期的光伏出力時序模擬，難以滿足電力系統靈活性規劃的要求。文獻[12]采用交叉譜法對可再生能源和負荷之間的相關特性進行分析，提出了一種雙鏈馬爾模型對負荷和可再生能源出力序列進行預測。但該模型建立在已有精度較高的未來負荷序列的基礎上，未能同時生成可再生能源和負荷的時間序列。

文中提出一種多鏈馬爾科夫-蒙特卡洛(Markov Chain Monte Carlo，MCMC)方法，采用統一的離散狀態定義將光伏出力序列轉化為反映大氣特征的離散狀態序列，簡化了仿真復雜度，建立了多條相互服從完全條件分布的馬爾科夫鏈來模擬光伏電站上空的隨機變化的大氣狀態，充分保留了光伏電站之間的相關特性。對3組不同相關程度的光伏電站仿真其出力序列，相較于傳統單鏈方法，該方法在生成任意相關程度的光伏電站出力序列時均能較好地模擬光伏電站間的相關特性，其生成序列的基本統計參數和歷史序列吻合度更高，驗證了該方法在考慮相關性的多光伏電站出力時間序列預測中的有效性。

1 考慮相關性的多光伏電站出力組合預測方法

光伏發電受到地球公轉和自轉的影響，日地距離和太陽高度角呈現周期性變化，因此光伏出力也呈現出明顯的規律性。和其他可再生能源相比，光伏出力主要呈現出季節特性與日特性、大氣特性和隨機波動特性這三大固有規律。在模擬光伏出力的固有規律的同時，考慮多個可再生能源對彼此出力不確定性的影響，基于MCMC法提出了考慮多光伏電站相關性的光伏出力序列的模擬方法。

1.1 數據處理

為了提高數據的準確性，需要對光伏電站的歷史出力數據進行預處理，剔除錯誤的測量數據，補全空缺數據。對于連續日的數據空缺，采用線性插值法對空缺數據進行差值；對于內部個別數據空缺，采用非鄰均值生成法進行填補。

1.2 多光伏電站相關性分析

利用相關系數分析多個光伏電站出力序列的相關程度，其計算方式為：

(1)

式中：X1，X2為任意2個電站出力序列；Cov(X1，X2)為序列X1與X2之間的協方差；Var(X1)為X1的方差；Var(X2)為X2方差。2個時間序列間的相關系數越大，其相關性越強。地理位置上越接近的光伏電站，太陽輻照情況相似度越大，則其光伏出力序列之間的相關性越強。相反，距離較遠的光伏電站出力序列之間的相關性較弱。一般認為，2個時間序列間的相關系數大于0.7，則其具有強相關性。

1.3 建立考慮多光伏電站相關性的光伏出力預測模型

根據各個光伏電站出力序列的相關程度，建立多鏈馬爾科夫模型，并對多個光伏電站的光伏出力序列進行預測，比較不同相關性程度下模型的預測效果。如果一個離散的時序過程在當前時刻的狀態僅由上一時刻的狀態所決定，該時序過程即是一個馬爾科夫過程。無云狀態下光伏出力序列的不確定性主要由大氣狀態所決定，而當前的大氣狀態和前一時刻的大氣狀態相關程度較高，因此可以采用馬爾科夫鏈表征大氣狀態序列。

由于鄰近地區光照情形類似，地區上空的大氣層狀況主要影響該區域內的光伏電站出力，因而光伏電站出力的不確定性受到周圍區域光伏電站出力的影響。為了將光伏電站出力之間的相互影響因素考慮在內，在多個馬爾科夫鏈之間引入相關性條件概率得到多鏈馬爾科夫模型，將某變量下一時刻的狀態看作該變量前一時刻的狀態及其他變量當前時刻狀態已知時的條件分布，對于多個光伏電站的出力進行模擬。

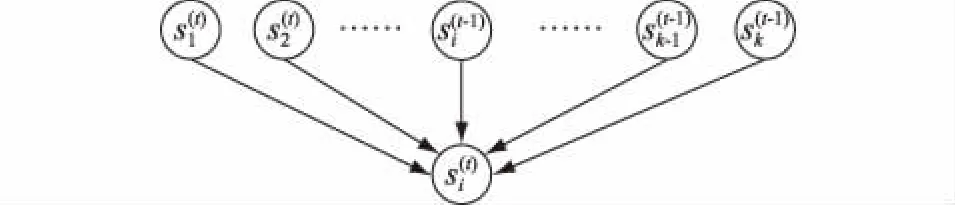
圖1 多鏈馬爾科夫過程Fig.1 Diagram of multi Markov Chain process

2 多鏈MCMC洛光伏出力預測模型

光伏出力預測模型包括離散狀態劃分、狀態轉移規律學習、蒙特卡洛狀態抽樣、光伏序列生成和修正四個部分。其具體流程如圖2所示。

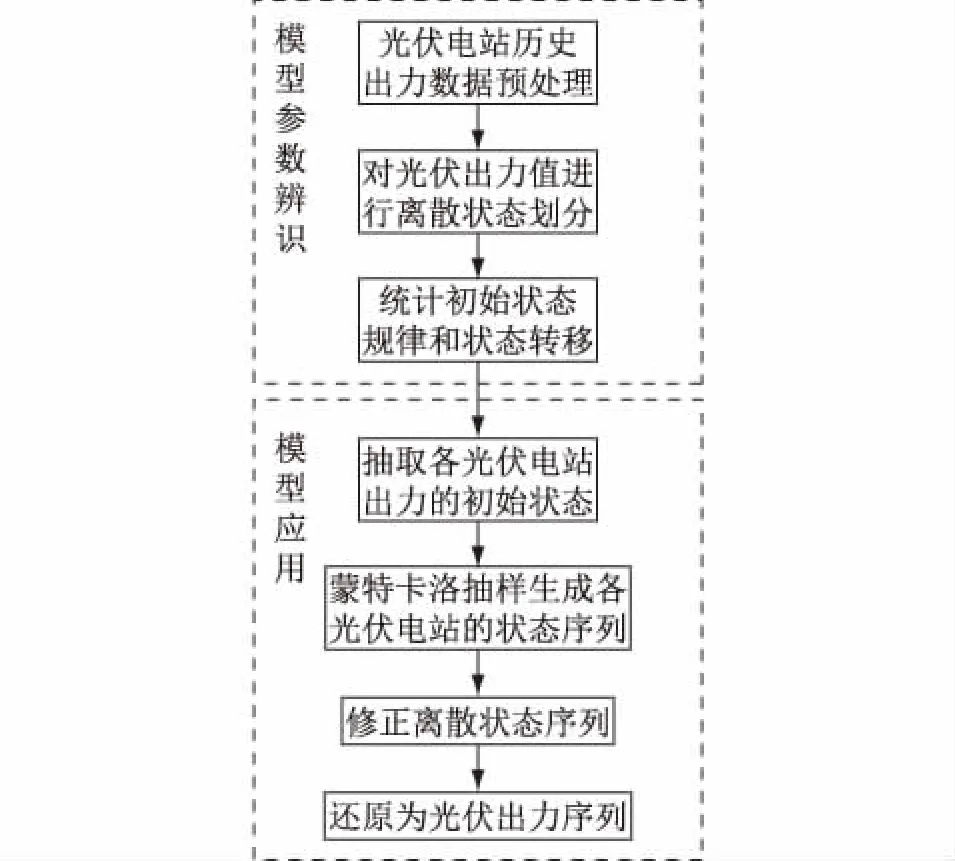
圖2 多鏈MCMC方法組合預測模型流程Fig.2 Flow chart of PV power time series forecasting process using multi MCMC method

2.1 離散狀態劃分

馬爾科夫鏈對應于一系列離散化的狀態，因而對各個光伏電站的歷史出力數據進行預處理后，將每一個發電功率值對應于特定的狀態。文中采用一種統一離散狀態定義的方法，避免傳統馬爾科夫模型對每個出力時段采用差異化的離散狀態劃分方法，降低了模型復雜度。離散狀態的定義包含兩個要素：出力范圍和離散狀態數。

離散狀態的選取要能反應光伏出力的季節特性和日特性，假定一定時段內大氣上空的太陽輻照度變化不大，可以將一年劃分為M個時期，將一天內光伏的有效出力時間劃分為T個時段，統計光伏電源在第m時期的每天第i個時段內的出力范圍為(Pm,i,min,Pm,i,max)，將該出力范圍劃分為N個離散狀態，每一狀態覆蓋的功率區間大小hm,i為：

(2)

該區間內某時刻的光伏出力P(t)對應的離散狀態s(t)(s(t)∈{1,2,…,N})為：

s(t)=[P(t)/hm,i]

(3)

由于光伏電池板接收到的能夠產生光伏出力的太陽輻照度主要受到大氣狀態的影響，因此N個不同的離散狀態對應于N種大氣狀態。從而12個月份的光伏出力功率可以采用統一的離散狀態定義，均轉化為1,2,…,N表示的離散狀態量，建立起一個歷史狀態序列。這種方法對于整個時間尺度上的歷史數據建立統一的離散狀態定義，進一步建立的狀態轉移矩陣無需區分季節和上下午時段，能夠大大減少模擬的規模。

2.2 狀態轉移規律學習

2.2.1 初始狀態規律

光伏出力的初始狀態包括出力開始時間和起始離散狀態。由于不同地區太陽輻照情況不同，為了使預測更加真實有效，模型在學習光伏出力歷史數據規律的過程中，需要對各個光伏電站的出力開始時間和起始離散狀態規律進行統計學習，便于后期抽樣生成各光伏電站每日出力的初始狀態。

2.2.2 狀態轉移過程

按照馬爾科夫模型的參數學習的統計估算方法，根據大數定律，在樣本數量足夠的情況下以頻率代替概率，計算各個狀態之間的概率轉移規律。

設某個區域內k個光伏電站的出力之間具有相關性，各光伏電站的離散出力狀態用k維變量s表示，s=(s1,…,si,…,sk),si∈(1,…N)，第i個光伏電站在t+1時刻的出力服從以下分布。

(4)

由上式構成的狀態轉移矩陣Pi，其維數為Nk×N。以k=2,N=3為例，s1服從分布。

(5)

s1對應的狀態轉移矩陣P1可以表示為：

(6)

其中：

(7)

2.3 蒙特卡洛狀態抽樣

抽樣生成服從完全條件分布的多條馬爾科夫狀態鏈的過程中，將狀態轉移矩陣作為抽樣中的完全條件分布，依次對各個變量進行輪流抽樣。抽樣的具體過程如下：

(1) 設定狀態轉移次數閾值n1，需要的樣本個數n2；

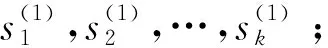
(3) Fort=1 ton1+n2

……

2.4 光伏出力序列的生成和修正

在多鏈馬爾科夫模型學習了歷史數據的狀態轉移規律的基礎之上，進一步采用蒙特卡羅抽樣方法生成離散狀態序列，需要將其還原為光伏出力值。大氣中云層的隨機移動、聚集和消散給大氣狀態帶來了瞬時擾動，為考慮這種隨機波動特性，需要在狀態序列中疊加白噪聲序列ψ進行修正。若某光伏電站某一時刻所處的離散狀態為s(t)，其所屬的時段為第m個時期的第i個時段，那么該時刻的光伏發電功率為：

P(t)=Xm,i,min+(s(t)-ψ(t))hm,i

(8)

3 算例分析

為了驗證多鏈馬爾科夫模型對于考慮相關性光伏電站出力建模的有效性，文中采用了美國俄勒岡地區6個光伏電站及我國寧夏地區光伏電站出力的數據進行仿真測試。美國俄勒岡地區的光伏電站的分布于4個區域，如圖3所示。

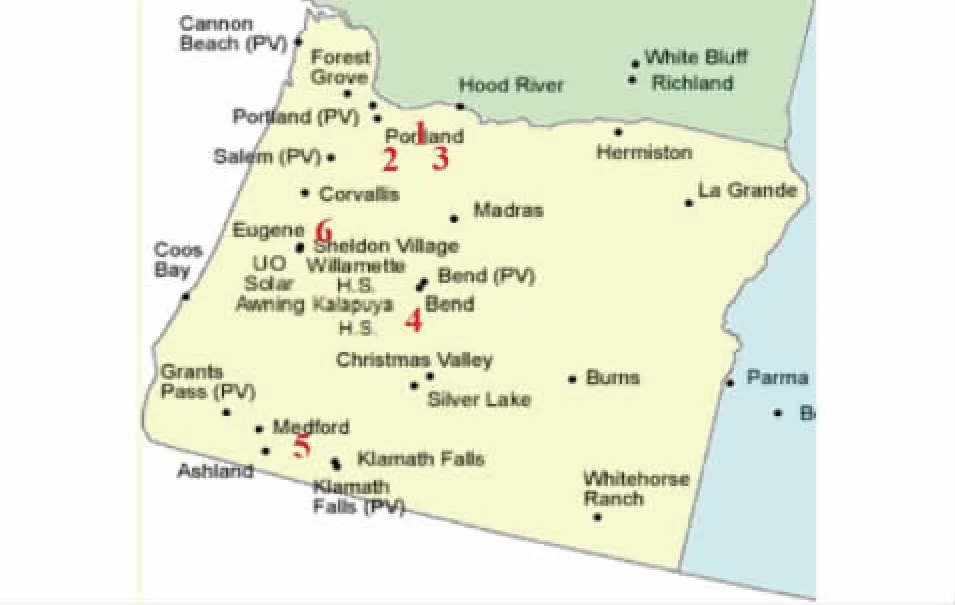
圖3 美國俄勒岡地區光伏電站地區分布Fig.3 Diagram of regional distribution of photovoltaic power plants in Oregon, USA

3.1 光伏電站的相關性分析

對本文選取的7個光伏出力觀測數據序列進行相關性分析，其出力序列的互相關程度如表1所示。

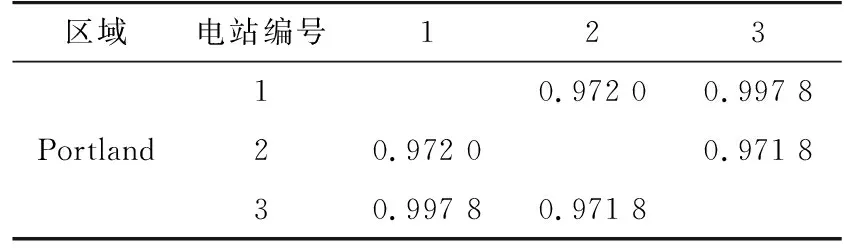
表1 光伏電站相關程度Tab.1 Correlation coefficients between PV power plants

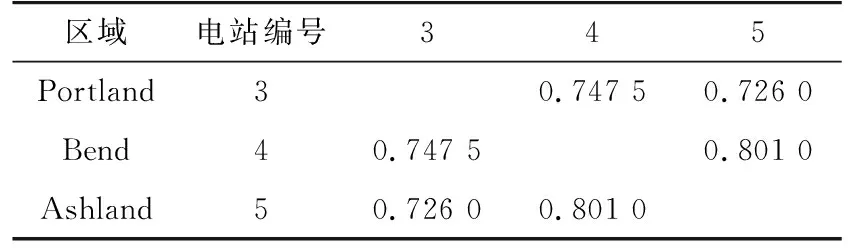
(b) 算例2

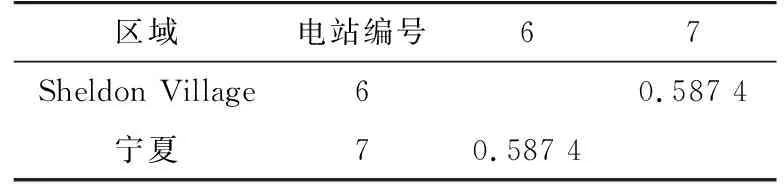
(c) 算例3

從表1中可以看出，Portland地區的3個光伏電站出力序列的相關程度超過0.9，呈現高度相關關系；分布于Portland、Ashland和Bend 3個地區的光伏電站的出力序列的相關程度均大于0.7，其相關程度小于集中位于Portland的3個電站；Sheldon Village地區和我國寧夏地區光伏出力相關系數較小，由于兩地區緯度相近，兩地光伏電站的出力仍具有一定的相關性。顯然，地理位置上越接近的光伏電站，地區上空的大氣層狀態之間的相互影響越大，其光伏出力序列的相關程度越強。

3.2 單鏈MCMC方法

采用單鏈MCMC方法對7個光伏電站的出力進行仿真模擬，離散狀態數選取為20，仿真時間長度為10 a。光伏出力的極限轉移矩陣約在1500～2000次達到收斂，設置狀態轉移次數的閾值為2000。

光伏出力序列的一般統計參數包括均值、標準差、概率密度函數和累積概率密度數。其中，概率密度函數和累計概率密度函數描述了光伏電站發電功率的長期概率分布。圖4中給出了各個光伏電站預測序列的一般統計參數對比，可以看出，單鏈MCMC方法預測的光伏出力序列能夠較好地繼承歷史序列的基本統計特性。

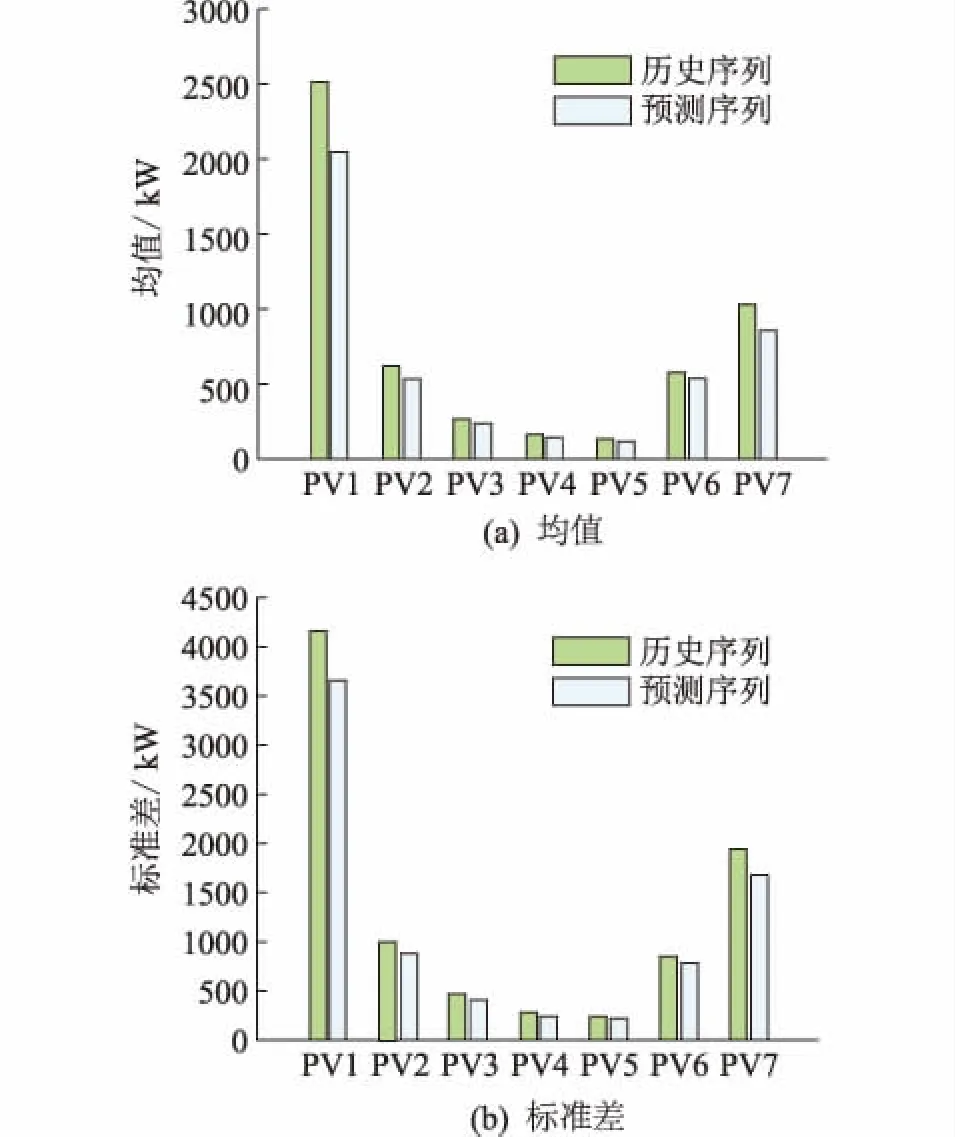
圖4 單鏈方法下7個光伏電站原始/預測基本統計特性對比Fig.4 Comparison of basic statistical characteristics of historical and predicted time series of 7 PV plants outputs using single MCMC method

從圖5中可以看出生成序列的概率密度分布和累計概率分布均和歷史序列十分接近，說明單鏈MCMC方法能夠較好地模擬歷史序列的分布效果。

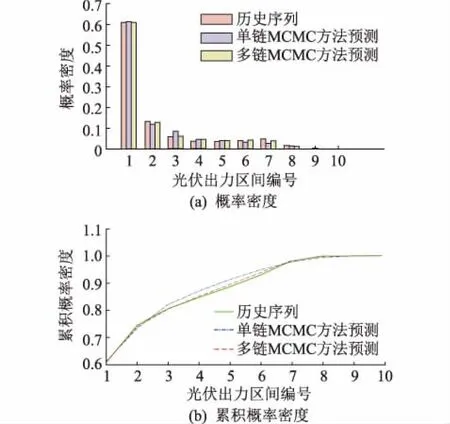
圖5 生成光伏序列概率密度和累積概率密度對比Fig.5 Comparison of probability density and cumulative probability density between single and multi MCMC method

3.3 多鏈MCMC方法

3.3.1 一般統計參數對比

采用多鏈MCMC方法對3組光伏電站出力序列進行仿真，其生成序列的一般統計參數和單鏈方法的對比如圖5和圖6所示，將光伏出力范圍等分為10個區間按從小到大的順序編號為1-10。從圖5可以看出，多鏈方法生成序列的概率密度和累積概率密度與歷史序列更為接近，更能體現歷史序列的統計特征。圖6描述了兩種方法所預測的序列相比于歷史序列的平均絕對百分誤差(MAPE)，從圖6中可以看出，光伏電站之間的相關程度越高時，采用多鏈方法生成的預測序列的均值和標準差相較于歷史序列的誤差越小，能更好地維持歷史序列的基本統計特性。但隨著組間光伏電站出力的相關程度的降低，多鏈方法的預測精確度有所降低，可能是因為相關程度較低的光伏電站在地理位置上相距較遠，大氣和云層之間的影響也較小。總體上，考慮相關性的多鏈MCMC方法在描述光伏電站的出力特性上仍然優于原始的單鏈方法。

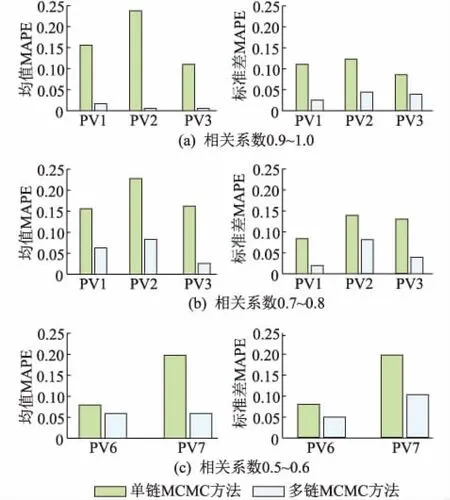
圖6 單鏈/多鏈方法下不同相關水平的 光伏電站預測序列和歷史序列的 基本統計參數對比Fig.6 Comparison of basic statistical characteristics of historical and predicted time series of PV plants outputs of different relevant levels between single and multi MCMC method

3.3.2 相關性參數對比

采用兩種方法預測3組光伏電站的出力序列的相關系數對比如表 2所示。

表2 單鏈/多鏈方法下不同相關水平的光伏電站 預測序列和歷史序列的相關系數對比Tab.2 Comparison of correlation coefficients of predicted time series of PV plants outputs of different relevant levels between single and multi MCMC method

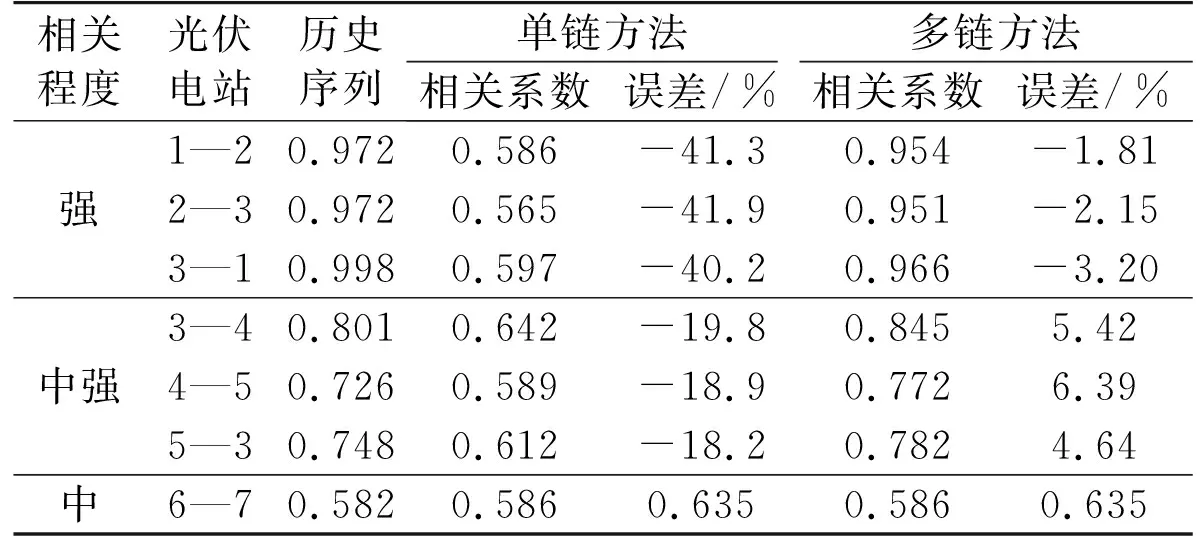
相關程度光伏電站歷史序列單鏈方法多鏈方法相關系數誤差/%相關系數誤差/%1—20.9720.586-41.30.954-1.81強2—30.9720.565-41.90.951-2.153—10.9980.597-40.20.966-3.203—40.8010.642-19.80.8455.42中強4—50.7260.589-18.90.7726.395—30.7480.612-18.20.7824.64中6—70.5820.5860.6350.5860.635

從表2中可以明顯看出，光伏電站之間的相關程度越高，多鏈方法所生成的預測序列保留原始序列之間相關性的效果越好。當光伏電站之間的相關系數較小時，單鏈方法和多鏈方法均能較好地繼承歷史序列之間的相關特性。這是因為光伏電站出力序列之間的相關程度由它們之間的地理距離決定，地理上相距越遠的電站，其上空的大氣狀態之間的影響也越小，此時單鏈馬爾科夫模型可以較好地刻畫各地區大氣狀態的隨機變化特性。而光伏電站之間的地理位置越接近時，它們的出力序列的相互影響越大，各光伏電站出力所對應的大氣狀態服從彼此之間的完全條件分布，因而此時考慮相關性的多鏈方法能夠更好地分析各個光伏電站之間的相互影響因素。

統計方法中，自相關系數常用來表示時間序列的前后相關程度，其計算方法如式9所示：

(9)

式中：Xi為時間序列；μ和σ分別為該時間序列的均值和方差；k表示時延階數。

單鏈方法和多鏈方法生成的預測序列的自相關系數對比如圖7所示，可以看出，多鏈方法預測序列的自相關曲線與歷史序列更加接近，能夠較好地保留原序列的時間相關性。

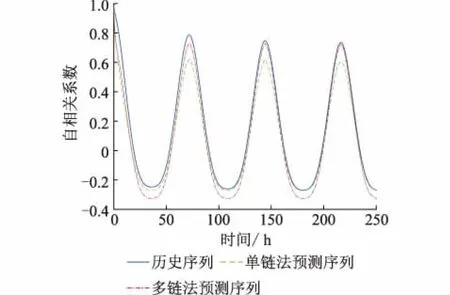
圖7 兩種方法光伏電站預測/ 歷史序列的自相關系數對比Fig.7 Comparison of autocorrelation coefficients of predicted time series of PV plants outputs between single and multi MCMC method

4 結語

文中提出一種考慮多光伏電站出力相關性的光伏出力序列預測方法。將多個光伏電站的出力序列轉化為反應大氣特征的離散狀態序列，辨識多條歷史序列的狀態轉移規律，建立多條相互服從完全條件分布的馬爾科夫鏈，對離散狀態的隨機波動特性進行修正后還原生成光伏出力序列。該多鏈MCMC方法應用于國內外7個具有不同相關程度的光伏電站功率序列生成，通過與歷史數據和單鏈方法進行對比分析，得到以下結論：

(1) 基本統計特性上，當一組光伏電站之間的相關程度較高時，多鏈方法較單鏈方法所生成的光伏功率序列，在均值和標準差上與原始光伏功率序列更為接近，在概率分布上更接近于原始分布，且對于相關性越強的光伏電站模擬準確度越高。

(2) 相關特性上，多鏈方法在預測不同相關程度的光伏電站的出力序列時，均能較好地維持光伏電站之間的相關特性，而單鏈方法不適用于相關程度較高的多個光伏電站出力序列的組合預測。

(3) 文中的多鏈MCMC方法適用于不同相關水平的光伏電站出力序列的組合預測，能夠繼承原始序列的基本統計特性，有效地體現多個光伏電站出力水平之間相互影響的特點。