把習題開發成課題 創造更多的“悟化成果”

/李相林

在習題教學中，能否以任務的方式進一步引導學生深入研究，帶領他們創造出一片未知的天地呢？下面，我們以舊版蘇教版教材五下中“”這道習題的教學實踐為例來進行探討。

一、重“點”，變習題為例題

這是一道比較單純的數學習題，完美地詮釋了幾何直觀的價值。學生初見驚嘆，但到后來，只要遇見“”就直接用1減去最后那個分數，其中不乏生搬硬套，其承載的幾何直觀能力培養的價值并沒有真正得以實現。由此，我們準備用任務的方式驅動學生“小題大做”一番。

我們首先變這道習題為例題，進行重“點”宣傳：一是讓學生在表示單位“1”的正方形中嘗試表示算式；二是讓學生把算式和圖形聯系起來想一想，原來的算式應該怎樣轉化？重點突出了幾何直觀的兩個關鍵——描述和分析（問題）。這樣一變，就變出了“直觀感知”的學習力，全班學生都能借助直觀圖來求解問題。在新版教材中，這道習題成了例題，與我們的嘗試不謀而合。

二、延“線”，變習題為專題任務

以任務驅動提升學生的數學研發力，需要突破淺表的“直觀感知”層面，向教學更深處——“直觀理解”延伸，將圖示與算式建立對應關系，理解圖示本身各部分間的關系，從而借助直觀圖分析、解決問題。

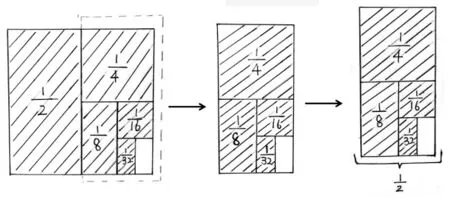
（圖1）

我們繼續據“點”延“線”，將這道習題設計成專題任務，以期獲得更多的“悟化成果”：（1）增加尾數：（2）變加為減：；（3）變增為減：。在題組任務探究中，學生受益于題（2），在用圖形描述難度系數較高的題（3）時，為了建立直觀圖和算式的對應關系，他們在原始圖上進行框注，分解出了新的圖示（如上頁圖1），進而用“”求出結果。

三、拓“面”，變習題為課題

“直觀推理”是“直觀理解”更高層面的發展，對學生特別是一些學有余力和學有潛力的學生的學習動力、毅力和能力的提升有著巨大的價值。認知心理學研究表明：當個體在某一方面有著豐富的知識經驗時，他就有可能進行更高級的思維。我們由“線”拓“面”，變習題為課題研究任務：怎樣運用直觀圖形分析、解決“”？按照這樣的思路，你還能求出哪些算式的結果？能寫出其中蘊含的規律并做出解釋嗎？讓學生以小組合作的方式在獨立思考的基礎上合力攻關。

1.研究課題，發展直觀洞察能力。

（圖2）

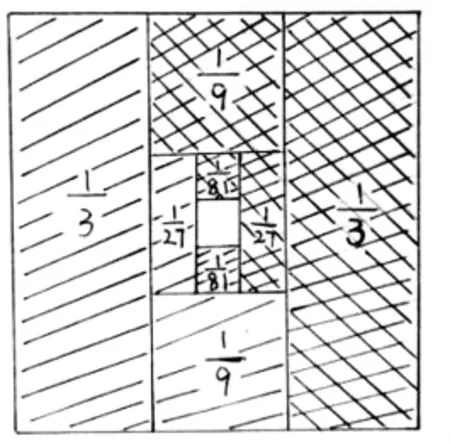
（圖3）

這個直觀圖的核心是“用簡單的空白部分間接求出復雜的陰影部分”，而讓空白部分變得簡單得可以直接表示是描述問題的關鍵所在，要想不出現新的空白，就得不斷給分數照鏡子，這樣每次剩下的空白部分就是正在表示的這個分數。學生給“”的直觀圖起了個形象的名字——“照鏡子圖”。

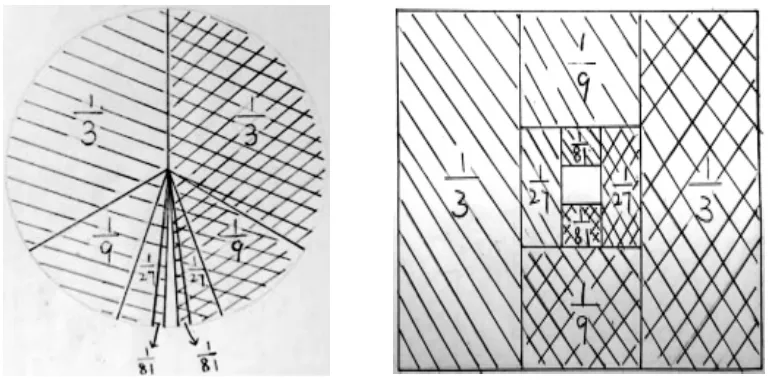
（圖4）

還有學生產生了新的“悟化成果”，提出用圓形和長方形也可以描述算式（如圖4），由此，學生認為，“”問題也可以用其他圖形或其他分法來描述。

為了完成這個高思維含量的任務，學生經歷了長時間的反復琢磨與嘗試，聚焦“空白點”，透過“”圖示中每次對應分數的自然形成，實現“”圖示中每次對應分數的人工促成，在圖形直觀上思考得更清晰、更深入、更合理，他們的數學研發力得到了實質性的提升。

2.研究課題，生長直觀推理能力。

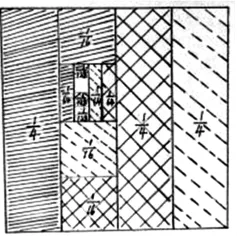
（圖5）

任務深入到這種程度，學生的幾何直觀能力達到了新的高度，他們沉浸其中，欲罷不能。對于后面的任務，學生自己如法炮制，由“”研創出“”的情形（如圖5）：；從而得出：；最終研創出這樣一個結論性的悟化成果：為≥2的自然數），這不就是關于幾分之一等比數列的求和公式嗎？

這種推理是建立在對直觀圖本質洞察基礎上的直觀推理，是借助直觀圖順利解決“”問題之后，在充分積累經驗的基礎上提出的。這個直觀圖可以是任何一個幾分之一的圖示，并通過由圖到算式的直觀推理直接提出關于“”的求和算式的算法。學生眼中的結論并非一道抽象的代數式，其背后隱藏著一幅直觀圖，用學生自己的話說，就是“整個圖形是幾（n－1）個自己（加法算式）與小空白的和，因此，求自己只要用‘1’減去小空白再除以份數即可”。這種直觀推理實質上是科學歸納推理，其核心是真正揭示了對象及其屬性間的因果關系，并以此為依據由點及面推出結論，雖未給出嚴格的演繹證明，但其中的分析成分又相當于演繹推理，學生對結論能給出令人信服的說明。

在變習題為課題的任務驅動式學習中，學生由特殊到一般趁勢融通，將豐富、深刻的認識提升到理性層面，其悟化成果達到了知識的高點，這在小學教學中無疑是難能可貴的，學生特別是一些學有余力和學有潛力的學生需要更多這樣的課題。