數學思維導圖應在何處“導”
/曹英芳
學生的學習過程具有形象思維與抽象思維、直覺與靈感、想象與創造互相結合的特點,這決定了他們在數學學習過程中需要一定的媒介來支撐思維的發展。美國圖論學者哈里說:“千言萬語不及一張圖。”學科思維導圖的出現順應了兒童思維發展的需要,它將思維的動態通過圖像、文字等符號形式表現出來,對提升學生的數學思維品質具有獨特價值。因此,數學思維導圖應關注知識本身的特點、學生的思維動態和課堂的互動情境,讓學生的思維向縱深處發展。
1.知識觀:導在知識繁難處。
從知識與技能的學習來看,思維導圖是一種掌握數學知識與技能的學習方法。思維導圖的繪制需要學生迅速找準關鍵主題,促使學生深入思考,依靠直覺理清知識的主干和分支,用圖形清晰而系統地展示出來。學生在“思—理—畫”的過程中,將數學思維的層次可視化,將繁難的知識變得有序、系統。例如:學生在解題過程中有時會出現解題步驟缺失、憑借主觀判斷增補或改變條件的現象。出現這種情況的原因可能是學生知識結構混亂、解題思路不清,而借助思維導圖則有利于幫助學生理清知識結構和解題思路,將所學的知識融會貫通,形成有序的思維邏輯。
2.學習觀:導在思維困頓時。
從學生學習的本質來看,數學思維導圖有助于引導學生進行思維建構,讓學生經過分析、類比、想象、判斷、反思等一系列的深度思維活動,尋找到數學問題的本質和解決問題的方法;可以讓學生在思維困頓時利用思維導圖,突破思維閥域,讓思維向縱深處發展。
例如:學習完蘇教版五下《圓的周長》一課后,教師可以設計習題完善知識結構:操場兩邊的圍墻相距157米,同學們用直徑1米的鐵環從操場的一端滾向另一端,鐵環能滾動50圈嗎?
大部分學生的解題思路是先求鐵環的周長:3.14×1=3.14(米),再求鐵環滾動 50 圈的長度 3.14×50=157(米),所以鐵環能滾動 50圈。產生這種錯誤的原因是學生混淆了周長的概念。鐵環前進的米數應該是圓心向前移動的米數,鐵環的出發點、停止點(即圓心)都是在距離圍墻0.5米(即半徑)處,也就是鐵環前進了(157-0.5-0.5=156)米。
在解題分析時,教師可以引導學生用圖畫出鐵環滾動一圈的情景(如圖1),再讓學生畫出鐵環滾動兩圈、三圈的思維導圖,最后學生由圖總結規律,推導出結論:兩端相距長度-半徑-半徑=鐵環滾過的米數(如圖2),以此理清了思維。
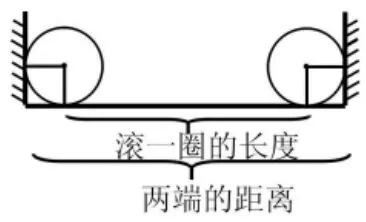
(圖1)
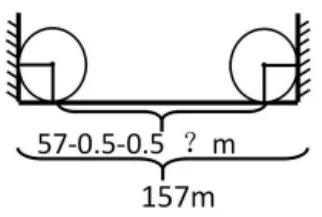
(圖2)
3.教學觀:導在互動關鍵點。
蘇霍姆林斯基說:“在人的心靈深處,有一種根深蒂固的需要,這就是希望感到自己是一個發現者、研究者、探索者,而在兒童的精神世界中,這種需要特別強烈。”數學思維導圖有著直觀、形象的特點,它能把復雜的關系條理化、清晰化。在課堂互動的關鍵節點利用思維導圖,有利于克服語言交流的抽象和空洞,促使師生、生生之間的交流更加生動有效,提升溝通和互動的深度。
例如:在教學“小數的加法”這一知識點時,筆者先讓學生結合整數的加法、估算等計算法則進行討論和交流,猜測和推算小數的加法運算法則。交流過后,有學生認為,小數加法的計算與整數加法一樣,計算時需要將末位數對齊;另一部分學生則認為,計算小數加法時要將小數點對齊,再進行計算。在爭論的關鍵時刻,可以引導學生利用思維導圖輔助猜測,將互動氛圍推向高潮:
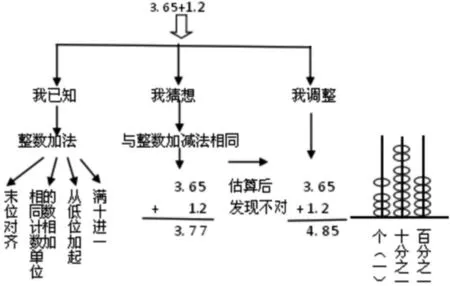
生1:請看我的預習思維導圖(如圖3)。
生2:我是這樣猜測——假設3.65元就是3元6角5分,1.2元是1元2角,加起來就是4元8角5分,就是4.85元。兩個數相加時,要把相同計數單位上的數相加,這和整數加法是一樣的。
(圖3)
生3:如果把相同計數單位對齊,那么就是小數點對齊了。
課堂互動時,學生圍繞思維導圖中的思路,運用類比、推理、估算等方法大膽猜測、嚴謹論證、表達觀點,在正誤的不斷碰撞中修正、調整自己的思維導圖,使學生對知識脈絡的認識逐漸清晰,對數學知識的理解也愈加深刻。
數學思維導圖是促進學生深度學習的有效方法,有助于發展學生的深度思考力,讓學生學會獨立學習和自覺學習。它更是一座橋梁,連接著知識、師生和思維,讓數學課堂教學成為“思維共振,情感共鳴”的交響樂!

