特征函數的性質在實變函數中的應用

石秀文

（邢臺學院，河北邢臺 054001）

在實變函數中討論集合的基數與對等、可測函數及函數的積分等問題時，常常用到特征函數，如果熟悉特征函數常用性質，并能熟練掌握應用特征函數的性質解決問題的一般思想，有助于提高學生分析問題和解決問題的能力。下面將探討利用特征函數的性質解決實變函數中某些問題中一般思想方法。

1 特征函數及常用的一些性質

1.1 特征函數的定義

顯然，若A是可測集S的可測子集，φA（x）則是S上非負可測函數，也是可積函數且

1.2 常用的幾個特征函數的性質

性質 1：設 A，B?S，則 A?B?φA（x） ≤φB（x），x∈S（單調性），φA（x）＝φB（x），x∈S?A=B（一對一性質）。

性質2：（特征函數與簡單函數的關系） 若f（x）=ci，x∈Ei，i=1，2…n，是 E 上的簡單函數，則 f（x）互不相交。

性質4：（積分等式）若f（x）在可測集E的可測子集E0及收斂，可測子集列En上可積，則有等式

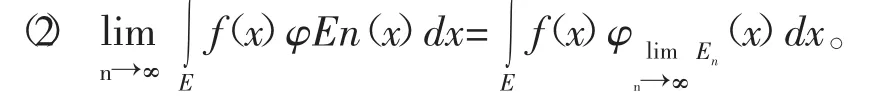
2 特征函數性質的應用

2.1 “一對一性質”在集合對等問題中的應用

集合的基數是集合的重要屬性，研究集合的基數是通過集合對等的關系來確定，建立集合間的——對應關系是確定對等的基本方法，如果難于建立集合間的一一對應關系，常用Bernstein定理來判斷對等并確定其基數。特征函數與集合間的一對一性質，對討論某些集合間對等有著重要的作用。

例1：設S是可數集，S的所有子集構成的集合為2S，求2S的基數。

解：由集合對等與基數的定義可知：對等集合的所有子集構成的集合族仍對等。不妨設為非負有理數集合為 S＝ ｛r1，r2，…rn，…… ｝，?A∈2S，令

設 φA（rn）=an，n＝1，2，3，……；令 x＝0.a1，a2，a3……，則 0≤x＝0.a1，a2，a3……＜1，即 x∈[0，1]。

由一對一性質，2S與 [0，1]的一個子集對等，所以（c為[0，1]的基數）。

反之，對?x∈[0，1]，可表示為唯一的無限小數0.b1，b2，b3……，可設對應的非負有理數構成的集

顯然，此映射是一對一的，故 [0，1]與2S的一個子集對等，所以綜上。

由此可見，通常討論某集的所有子集構成的集合2S的基數問題或集合族與其他集合對等問題時，可考慮應用定義在S上關于其子集的特征函數，通過特征函數“一對一”性質，建立2S與相關集合或其子集的一一對應關系來解決問題。

2.2 可測函數與特征函數的關系的應用

可測函數與簡單函數的關系：f（x）是可測集E?Rn上可測函數的充要條件是存在一列簡單函數ψm（x），使得

而由性質2可知簡單函數ψm（x）是一組特征函數的線性和。因此，討論可測函數問題，就可以歸結為最簡單的特征函數問題，“由特征函數到簡單函數，再向一般可測函數過度，這在許多場合都是行之有效的辦法。”

例 2：設 f1（x）、f2（y）分別是 E1?Rp、E2?RqS上可測函數，證明：f1（x）×f2（y）是 E1×E2?Rp×Rq上可測函數。

解析：證明有具體表達式函數的可測性，用定義直接證明較為簡便；證明抽象函數可測性，可考慮用“可測函數與特征函數的關系”進行推理論證。

設f（x，y）=f1（x）×f2（y）

（1）若fi（x）是可測子集Ei上特征函數，則f（x，y）是E1×E2上特征函數，可測集上特征函數是可測函數，故結論成立。

（2）若fi（x）是Ei簡單函數，則f（x，y）是E1×E2上簡單函數（易證），故是可測函數。

（3）fi（x）是一般可測函數，由可測函數與簡單函數的關系，存在簡單函數列 gm（x），hm（y），使得：f1

令 ψm（x，y）=gm（x）×hm（y），也是 E1×E2上簡單函列，且

故結論成立。

此例證明思路是由簡單到復雜，即由特征函數成立——簡單函數成立——一般可測函數成立，這種由特征函數逐漸遞進到一般可測函數的證明，是實變函數中常用的方法。

2.3 特征函數積分性質的應用

設f在E及其可測子集E0上可積，常用的兩個等式：若存在，由控制收斂定理及極限性質：

證明：對任意可測子集A?E，φA（x） 在E有界可積，故由A的任意性可知：

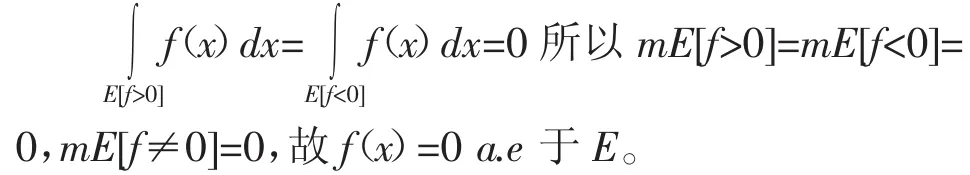
可見利用等式（1）通過特征函數巧妙的將E上的積分轉化為其任何子集上的積分使其為零，體現了特征函數在積分問題中的作用。一般的，當涉及到某集合上的積分與之子集上的積分關系時，可考慮應用這一性質進行轉化。

例4：設函數f在E上可積，可測集列En?存在，則

（2） 由可積性知，f在En上可測，而[a，b]，故 f在 [a，b]上可測.構造函數列：fn（x）＝φEn則fn（x）在E上可測，由En?En+1，由特征函數單調性，可知 fn（x）≤fn+1（x），所以 fn（x）→f（x）于E。

例6：若設f，g在可測集E上非負可測，則對?a∈R1，mE（f≥a）＝mE（g≥a），則

解析：E＝E[x；f（x）≥0]＝E[x，g（x）≥0]，

（2） 否則f，g在E上幾乎處處有限（不妨設處處有限），由已知條件可知：mE（a≤f≤b）＝mE（a≤f）-mE（b≤f）＝mE（a≤g≤b），?a，b∈R1。于是?n，令 En＝E[0≤f≤n]＝E[0≤g≤n]，Fn＝E[n≤f]＝E[n≤g]，E＝En∪Fn

?n，將En作互不相交分解：其中，令 Fn＝En，n2*，由集En，k的特征函數來構造E上單調遞增簡單函數列：（x），則?x∈E，?n，使得f（x）∈[0，n]

此例中，利用特征函數構造如上的簡單函數列，該函數列在E上收斂于可測函數f（x），這是實變函數中特征函數應用的一個典型的方法，對討論某些可測函數與積分問題有著重要作用。