小學數學中的合情推理
耿云芬
(云南省昆明市呈貢區第二小學 云南昆明 650500)
數學是講求邏輯的,是思維性的科學。但從各種事實證明,數學的許多新發現、新發明是在猜想、證明之后產生的。而合情推理是猜想、證明的先導。我要與大家一起探討的就是基于直覺思維基礎上的合情推理。
一、合情推理及其相關內容
合情推理按字面理解就是合乎人的情理的推理,是直覺的反映。其主要特點是:推理依據的條件和結論之間的關系不一定具有邏輯性而僅僅依靠直覺。
數學中的合情推理是多種多樣的,其中不完全歸納推理和類比推理是兩種用途最廣的特殊合情推理。①不完全歸納推理是根據考察一類事物的部分對象具有某一屬性,而作出該類事物都具有這一屬性的一般結論的推理。②類比推理是通過對兩個或兩類不同的對象進行比較,找出它們的相似點,近似程度,然后,以此為根據,把其中某一對象的有關知識或結論推移到另一對象中去,這就是類比推理。
二、合情推理在小學數學學習中的意義
首先,是實施新課標的需要。《數學課程標準》中明確:歸納和類比是合情推理的主要形式,并指出:第一學段“初步學會選擇有用的信息進行簡單的歸納和類比”,第二學段“進行歸納、類比與猜測,發展初步的合情推理能力”,第三學段“體會證明的必要性,發展初步的演繹推理能力”。其目的是有序地培養學生的推理能力,但小學階段以發展學生初步的合情推理能力為主要目標。其次,是由小學生的年齡特征和認知特點決定的。鑒于小學生的年齡與認知特點,他們不可能通過嚴格標準的邏輯推理來發現和掌握數學規律和知識。因此,在教學中大量地采用合情推理的方法。
再次,是學生學習數學的過程要求。在數學學習的過程中,應給學生提供具有充分再創造的通道,以激勵學生進行再創造的活動。把數學知識學習的過程展開、還原,讓學生經歷觀察、比較、歸納、類比……即合情推理提出猜想,再驗證出猜想正確或錯誤。
三、合情推理的兩種基本形式及小學數學學習中的運用
1.不完全歸納法
從特殊到一般,從個別事物中概括出一般規律,一般使用不完全歸納法。
(1)歸納定律

兩個數的和與一個數相乘,等于把這兩個加數分別同這個數相乘,再把兩個積加起來,結果不變。這就是乘法分配律。
(2)發現規律
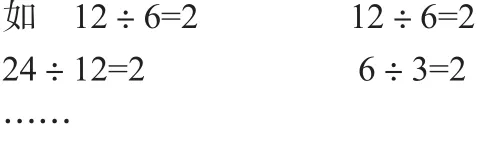
歸納出:被除數和除數同時乘或除以相同的數(0除外)商不變。
(3)抽象數量關系
如:一本書15元,3本書多少元?列式:15×3=45(元)
一個杯子8元,9個杯子多少元?列式:8×9=72(元)
……
歸納出:總價=單價×數量
(4)找到解題技巧,提高解決問題的能力
例如 計算小于1000的所有自然數的和
本題實際上是求 1+3+5+7+9+……+997+999的和
在自然數1~1000中奇偶數的個數各占一半,所以上面的算式共有500個奇數相加。

我們歸納發現:從1開始連續n個奇數的和恰好等于n2。
因此得到:1+3+5+7+9+……+997+999=5002
不完全歸納法可以幫助人們去發現真理,啟發人們猜想,但結論具有或然性,這是不完全歸納法的兩重性:可以得到偉大的發現。
不可否認的是:雖然不完全歸納法的結論具有或然性,但它是探究數學規律的重要方法。在教學中,尤其是在低年級教學中不完全歸納法有廣泛的應用。要教給學生一些知識而又不想進行嚴格邏輯證明時,一般都采用不完全歸納法。
2.類比推理法
因為類比推理是允許在不知它們之間是否有必然聯系的前提下進行的。因此,同樣是運用類比推理得出的結論,有的可能是正確的,有的則可能是錯誤的。在教學中應強調經過類比的結論必須由實驗檢驗,或用其它論證方法予以證明。
例如:在推到圓錐的體積公式時,由于學生已經具有圓柱的體積知識,教師先引導學生觀察等底等高的圓柱和圓錐。再讓學生猜想等底等高的圓柱和圓錐的體積有什么關系?學生通過觀察、比較、歸納、類比……即合情推理提出猜想。于是老師引導學生通過實驗來驗證自己的猜想,最后得出結論:圓錐的體積等于等底等高的圓柱體積的三分之一。我們通過合情推理提出猜想,再通過實驗驗證得到結論,推到出圓錐的體積公式。掌握知識的過程符合小學生的年齡特征和認知規律。
新課程改革要求學生全面發展,不僅要掌握知識,還要會發現問題,解決問題。因此,在教學中,教師應有意識的培養學生合情推理的能力。使學生能夠根據數學的直覺得到一些數學的發現,從而讓學生品嘗到一些成功的喜悅,提高他們對數學的學習熱情和信心。這可以提高課堂教學質量,而且還可以培養學生的創新精神。

