基于MIDAS對橋梁荷載試驗的應用研究

謝棟明，王艷軍

（福建農林大學金山學院，福建 福州 350000）

0 引言

改革開放以來，國內各種政策大大加大了資本對基礎設施進行大量投資的意愿。在大修基礎設施的背景下，各種新項目如雨后春筍一般，甚至使得中國近幾十年修建的橋梁數量超過了過去幾千年各時期建造的總和。各種結構型式可供選擇，橋梁施工技術水平逐漸達到世界一流水平。隨著工程總體技術的增長，測試橋梁安全穩定的技術也隨之增長，橋梁的評估也變得越來越科學規范。

國內外橋梁建設現狀各不相同，但不論是在發展中國家還是在發達國家，基礎設施建設一直是國家建設的重點。在美國、英國等發達國家，陸上公路橋梁運輸比率逐年增長[1]，并且還有繼續增加的趨勢。相對國內而言，國外起步較早，經過長時間的積淀，建立了嚴謹的科學體系，施工步驟逐漸合理規范，在技術上擁有領先地位，建造出了許多難度頗高的大跨徑橋梁，例如位于美國西部的科羅拉多大橋，其橋身整體結構距離科羅拉多谷底約為一千兩百多米，可以同時承受約兩萬游客的重量。此外，位于英國的蓋茨亥德千禧橋，是世界上第一座也是目前唯一一座傾斜橋。中國的橋梁建設雖起步晚，處于落后地位，但在建設技術上奮起直追，整體工程建造技術發展速度驚人，加上國家在政策上大力扶持，到目前為止，在分析石拱橋，桁式拱橋，雙曲拱橋，鋼筋混凝土拱橋，預應力混凝土斜拉橋，連續剛構框架結構上，行業整體的研究越來越深入；連續梁橋等特殊的評估加固技術，橋梁穩定性評估，加固質量檢驗和評估方法，高粘結度抗擾建筑材料等新材料的研究也越來越成熟。在這類更為進步的專項研究中，將使得國內的橋梁安全性檢測研究和對測試為通過橋梁進行處理的方法會越來越科學合理。

此項研究就是針對國內存在著難以適應現代交通負載和運輸需求的橋梁而進行的。并且隨著近年來網絡電商異軍突起，物流業高速發展，對公路橋梁的荷載能力和養護要求有了更高的挑戰。部分國內橋梁的承載能力和承載力尚遠遠不能滿足現代交通條件的要求。如果對所有這些橋梁都要拆除和重建，毫無疑問將需要花費大量的資金和人力，短時間內缺少這些橋梁，通行能力將嚴重下降，并且會使交通秩序變得十分混亂。如果我們能夠充分地利用現有資源，通過可行的檢查和評估方法對可能的橋梁進行穩定性研究，例如利用Midas-civil程序模擬存疑的橋梁在靜力荷載和動力荷載作用下的穩定性[2]，并且結合實際情況，判斷研究方法是否可行。然后對存在問題的橋梁采取相應的重建或加固措施，延長其使用年限，就能大大節約社會成本，還能保證交通運輸安全穩定。

本文的研究依據橋梁的荷載試驗進行橋梁穩定性判斷，其中包括動力荷載和靜載試驗。橋梁檢測荷載試驗是將國家公路橋梁規范中的標準設計荷載施加于橋梁結構的指定位置[3]，測量橋梁在其影響下的相關參數。靜載試驗主要是觀察靜載荷下橋梁結構的靜位移和靜應變。動荷載試驗主要是觀察橋梁結構在選定激振作用下產生的振動圖形數值，以此來觀測橋梁振型，分析橋梁的動力特性。本次研究結合橋梁結構有限元分析軟件Midas-civil及現場實際試驗數據對某地鋼筋混凝土板橋進模擬分析，還將對其運行條件進行全面評估，為測試橋梁載荷測試提供依據。

1 工程概況和整體設計

該鋼筋混凝土板橋基本情況為：跨徑為8m，橋寬為6m。上部結構采用GB10（RC）的C40混凝土橋面板，橫向布置面設置8片混凝土矩形板，采用GB12(S)的Q345型鋼筋，分別布置橫向梁和縱向梁。

2 使用Midas-civil建立有限元模型

該板橋采用有限元計算軟件Midas-civil建模。采用用梁格法建模,坐標系選取默認坐標系，單位系選取ton/m。材料上，選取T字型和工字型的Q345型鋼筋，截面分別為 TM 297×302×14/23，HP 502×470×20/25；混凝土采用C40；結構上，豎向兩端設置工字型HP 502×470×20/25，中間布置三段截面為T字型TM 297×302×14/23縱梁，橫向布置九段工字型HP 502×470×20/25橫梁，上部結采用橫向設置 8 片厚度為0.3m的C40混凝土矩形板，共計 85個節點，102個梁單元，8個板單元。

3 計算過程及結果分析

3.1 靜力荷載分析

3.1.1 計算原理

測點變位與應變的計算。根據量測數據做下列計算查公路橋梁荷載試驗規程得到位變計算公式如下：

總應變：St=Sl-Si

彈性應變：Se=Sl-Su

殘余應變：Sp=St-Se=Su-Si

在式中，Si為加載荷載前的數值；S1為施加荷載后達到穩定時數值；Su為去除荷載后達到穩定時數值。

為了得到評測橋梁穩定性的可用的計算結果，需對相對殘余位變進行計算;相對殘余變位按以下公式計算：

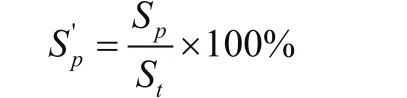
基于在測量點處測得的應變，當結構處于線性彈性作用狀態時，能夠計算測量點處的應力[4]。

3.1.2 單車加載情況

在單車分別加載情況下, 取一組車輛組合進行加載，將荷載轉化為質量后，進行分析，查看輸出結果，觀察后發現車輛加載范圍內應變較大, 并且逐漸衰減, 大部分是中間部分參與受力，邊緣兩塊板不參與縱向受力, 共同受力狀況較差（見圖1）。

造成這種情況的原因可能是橋結構之間連接、板之間縫隙接頭不合理等結構問題。

采用三種車輛分別進行加載時，橋梁的應變數值呈比例型增長, 此情況說明了受力板塊是處于正常受力狀態中的, 由此判斷結構局部受力情況良好[5]。

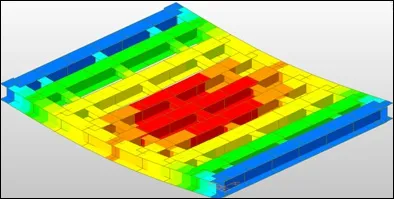
圖1 單車加載情況圖Fig.1 Cycling loading diagram

3.1.3多車加載情況

多車情況的加載為雙車道同時進行加載。將三種類型車輛組合分別組合進行加載，利用Midas結果輸出圖表數值查看計算結果，觀察結果可知車輛的加載范圍應變值較大，中間板塊應變向外擴散開始漸漸降低，應變變化較為明顯，由此可得該結構的共同受力情況較差，其原因多與單車情況相似，可能為結構連接處設置不合理[6]。

在多車加載情況中，其應變模式也呈比例增長，兩種工況的應變增長都合理進一步說明了結構處于受力狀況良好的狀態（見圖2）。

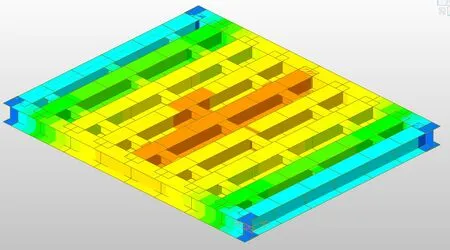
圖2 多車加載情況圖Fig.2 Multi-vehicle loading situation diagram

3.1.4 靜力加載情況分析

將兩種加載情況理論計算結果與實測結果進行對比后發現，在測試的結構中，Midas模擬所得的理論變形位移情況，其數值與的實際工作狀態在車輛加載范圍的變形量基本一致；但存在部分結構上理論應變值與實測應變值有較大差距的問題（見圖3），結合橋梁實際使用情況，原因可能為該橋長期處于較大交通荷載壓力下，在多年使用后板橋結構已經受到了一定程度的破壞，導致了該鋼筋混凝土板橋應變分布不均勻[7]。

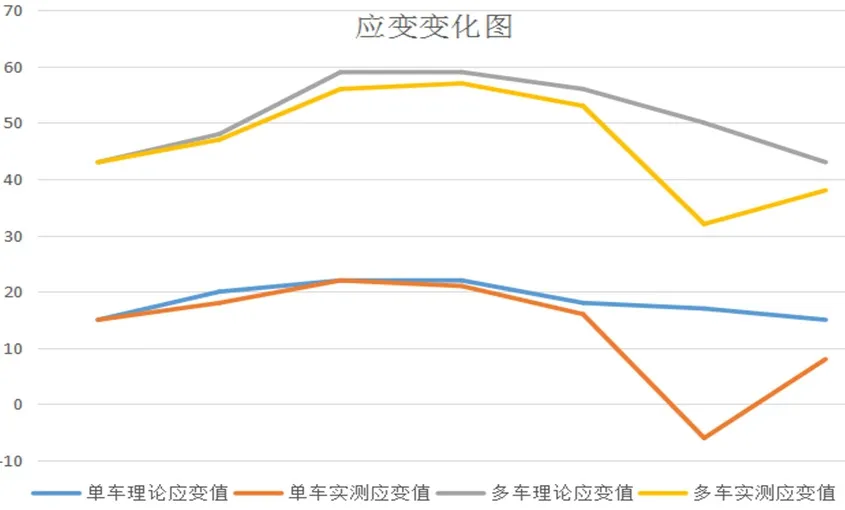
圖3 應變變化圖Fig.3 Strain change diagram

分別進行單車輛荷載和多車車輛加載后，觀察圖表數據，發現僅有處于加載范圍內的部分結構參與受力，并且有在結構兩端梁上受力較小，說明此整體結構設計不合理[8]。另一方面從參與受力的結構來看，參與受力的測試截面應變值最終能夠到達穩定數值，加載荷載時，變位程度也在合理范圍之內，并且在兩種工況下車輛荷載進行加載時，結構的截面應力都呈彈性線形增長。由此可看出單處結構橋面板的的受力性能良好，但是結構整體受力轉態較差[9]。

3.2 動力荷載分析

3.2.1 理論分析

通過查詢公路橋涵設計通用規范, 得到規范中的計算公式，用其對簡支板橋基頻理論計算值進行計算。簡支混凝土梁板橋理論頻率計算公式為：

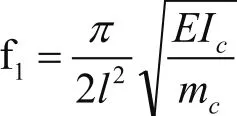
mc=G/g

上式中：

L為結構的計算跨徑(m)；E為結構材料的彈性模量(N/m2)；

I指構造跨中截面的慣性矩；mc指結構跨中處單位長度的質量(kg/m)；

G指跨中處每延米的結構重力(N/m)；g為重力加速度，g=9.81(m/s2)。

3.2.2 實測動載數據分析

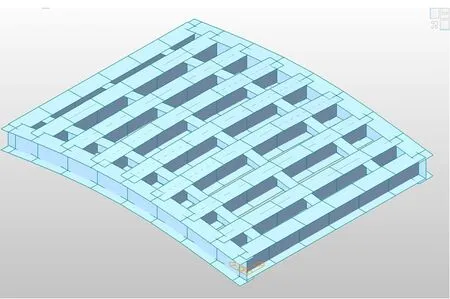
圖4 模態1Fig.4 Modal 1

使用Midas-civil模擬加載移動荷載，規范選取中國橋梁道路規范，荷載系數取0.97。使用橋梁分析軟件，建立該有限元模型[10]，特征值計算選用Ritz向量法,對橋梁進行特征值計算，查看軟件的特征值分析表（表1）可得到該簡支混凝土板橋的前兩階頻率為:第一階頻率f1=3.40Hz；第二階頻率f2= 8.02Hz。

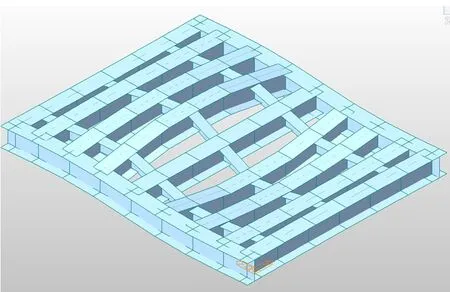
圖5 模態2Fig.5 Modal 2

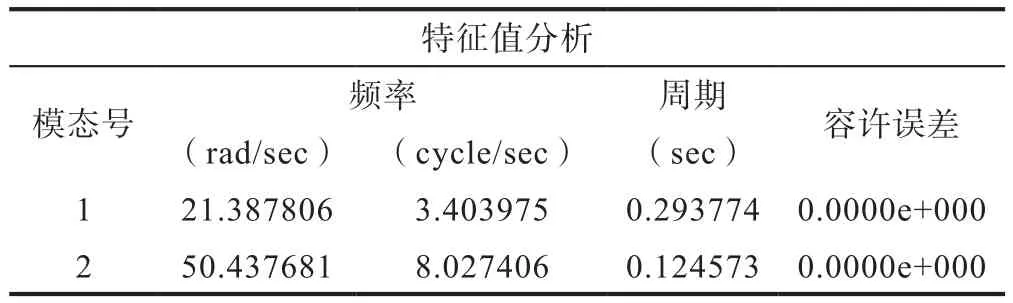
表1 特征值分析表Table 1 Characteristic value analysis table

動荷載試驗擬采用3號車，采集跑車狀態下橋梁結構的動力響應，加載車輛分別以10km/h和15km/h的速度無障礙通過該鋼筋混凝土簡支矩形板橋，使用Midas-civil對板橋模型施加移動荷載時，得到板跨中截面的實測震動頻率值為3.353Hz，模態1中的一階頻率計算值差異較小，且計算得到的理論計算值大于實測值，表明該混凝土板橋的動力性能情況良好[11]。

4 結論

綜上所述，該橋在實際使用健康檢測和維護過程中存在問題，橋梁結構已經不能承擔過大的交通壓力；以及利用Midas-civil模擬多單元多節點的橋梁可行的，能夠為橋梁的安全使用提供可靠的依據；在將來的橋梁建設發展中，此方法可以應用到實際當中中去，在橋梁安全性檢測中起到重要的參考作用。