綜合多信息的高精度變差函數擬合優選分析：以塔中4東河砂巖油藏為例

尹楠鑫，江同文，徐懷民，徐朝暉，羅 超，陳 岑

(1.重慶科技學院石油與天然氣工程學院，重慶 401331； 2.中國石油塔里木油田分公司，新疆 庫爾勒 841000； 3.中國石油大學(北京)地球科學學院，北京 102249)

0 引 言

儲層建模技術發展至今始終面臨著井間預測的不確定性問題，而引起不確定性問題的原因，主要歸結為以下幾個方面[1-4]：①已知資料的不完備；②已知資料的精度不夠；③對儲層的認識程度不夠；④建模算法不夠完備。但對于影響建模精度的至關重要的變差函數分析，常常被人們忽視，尤其在大井距的地區，擬合變差函數的樣本數據點空間相關性差，數據結構不穩定，難以擬合出理想的實驗變差函數曲線，這將會極大影響最終建立的三維地質模型的準確度[5-12]。因此，如何充分利用已有的井筒及三維地震資料開展變差函數分析，并將對比優選的變差函數結果運用于三維地質建模研究，是一個值得探討的問題。本文以塔中4東河砂巖油藏為例，通過利用水平井資料和地震資料開展的變差函數優選分析，剖析了水平井和地震資料具有豐富橫向信息的優越性，為建立高精度的三維地質模型奠定基礎。

塔中4油藏位于塔里木盆地塔中10號構造帶東端，是在前石炭系剝蝕面上形成的大小不同形態各異的披覆背斜之一，東臨TZ16油藏，東南緊靠塔中1氣藏，面積290.88 km2。地理位置位于新疆維吾爾自治區巴音郭楞蒙古自治州且末縣境內(圖1)，地表為復合型縱向沙壟，與油田長軸垂直，氣候極干旱。1992年4月由塔中4井中途測試發現了塔中4油田。經后期勘探開發證實，塔中4油田是塔克拉瑪干沙漠腹地發現的第一個整裝油田，其主力產油層為“石炭系東河砂巖段”(早期東河砂巖現今已經被進一步劃分為“含礫砂巖段”和“東河砂巖段”兩個巖性段)，發育淺水三角洲相、濱岸相及潮坪相。張惠良等研究認為塔中4井區位于沉積盆地的東部邊緣，在其北東及南東分別為兩大古陸剝蝕區，在這兩個剝蝕區之間為一寬約30 km的以發育河流水系為主的大山谷，發育有河流-三角洲沉積體系、濱岸沉積體系、潮坪沉積體系[13]。東河砂巖是一套海侵背景下沉積的砂體，受相對海平面變化影響，共發育5期砂體，且5期砂體具有分區性，塔中4井區主要發育第2期、3期砂體。塔中4油田整體呈南東走向的長軸背斜構造油藏，發育TZ402、TZ422、TZ401三個構造高點，高點間以鞍部相接或斷層分割。五個油藏，自上而下包括CI、CII、CIII三套含油層系，含油面積21.4 km2，儲量3 765×104t。累積核實產油量1 480.2×104t，采出程度38.6%，綜合含水75.3%。

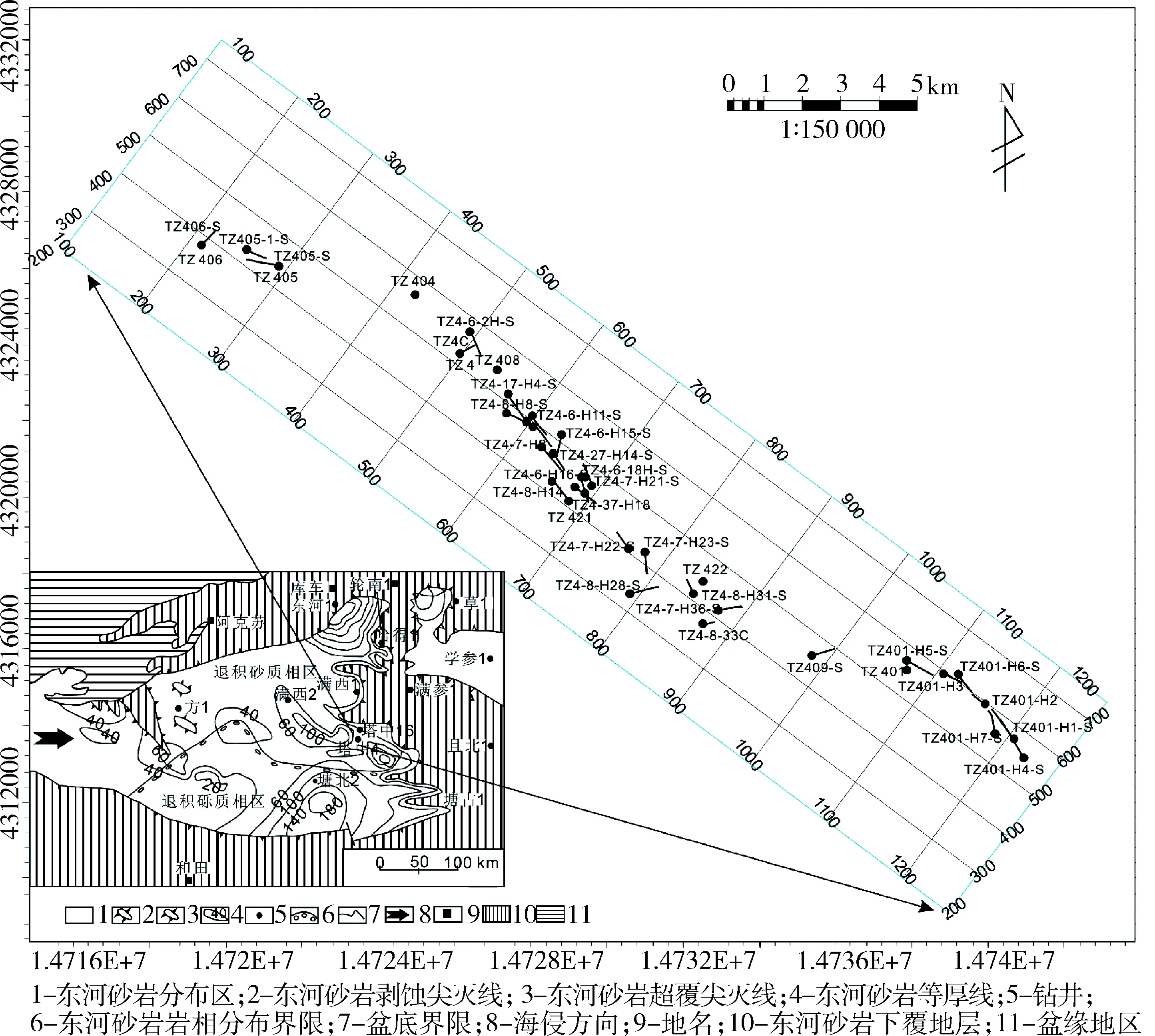
圖1 工區位置及塔里木盆地東河砂巖分布特征(資料來源：東河砂巖平面分布圖引自王招明等[14]，2004年，有修改; 注：井名顯示所有的水平井和部分直井)

本次研究目的層為含礫砂巖段和東河砂巖亞段兩個巖性段，由下往上依次發育三角洲、濱岸相以及淺水三角洲等幾種大的相類型，在對研究區地層對比的過程中,以層序地層學理論為指導，以不整合界面為層序的邊界，確立整體對比框架；采用沉積旋回對比法，把同一沉積時期、沉積厚度相近、電測曲線特征相似的地層劃分為同一層。通過分級控制，旋回對比的方法，研究區目的層被劃分成了14個小層。

塔中4油田目前已進入開發中后期，油田產量急速遞減、含水率快速上升，開發效果變差，階段穩產形勢嚴峻。要保持產量或增加油氣產量，亟需通過地質、測井以及新采集處理的三維地震資料建立高精度的三維地質模型，來開展精細油藏描述工作，以期解決油田開發過程中地質認識不清等問題，從而為油田后期剩余油的挖潛、開發方案的調整及開發效果的提高奠定基礎。油藏埋藏深度大都在3 600～3 720 m，由于采用不規則井網，井距大多大于600 m。主力產層含礫砂巖段砂體厚度薄，基本上都小于5 m，且隔、夾層發育，井間不易追蹤，難以建立精細的三維地質模型。塊內有各類井125口，其中水平33口，2012年新采集處理的三維地震資料428 km2。

1 變差函數基本原理及其參數意義

變差函數是地質統計學用來描述區域化變量空間相關性的工具，也是地質統計學的三大理論基礎之一，把一個地質體看成是空間中的一個域V，V內的x、x+h是沿某一方向相距h的兩個點，其觀測值分別為Z(x)和Z(x+h)，二者的差值就是一個有明確地質意義的結構信息，因而也可以看成是一個變量，如果沿x方向有被相同矢量h分割為許多點對時，即可得到上述的一組差值，而該差值的平方的期望即為變差函數[15-16]，見下式。

r(x,h)=1/2E[Z(x)-Z(x+h)]2

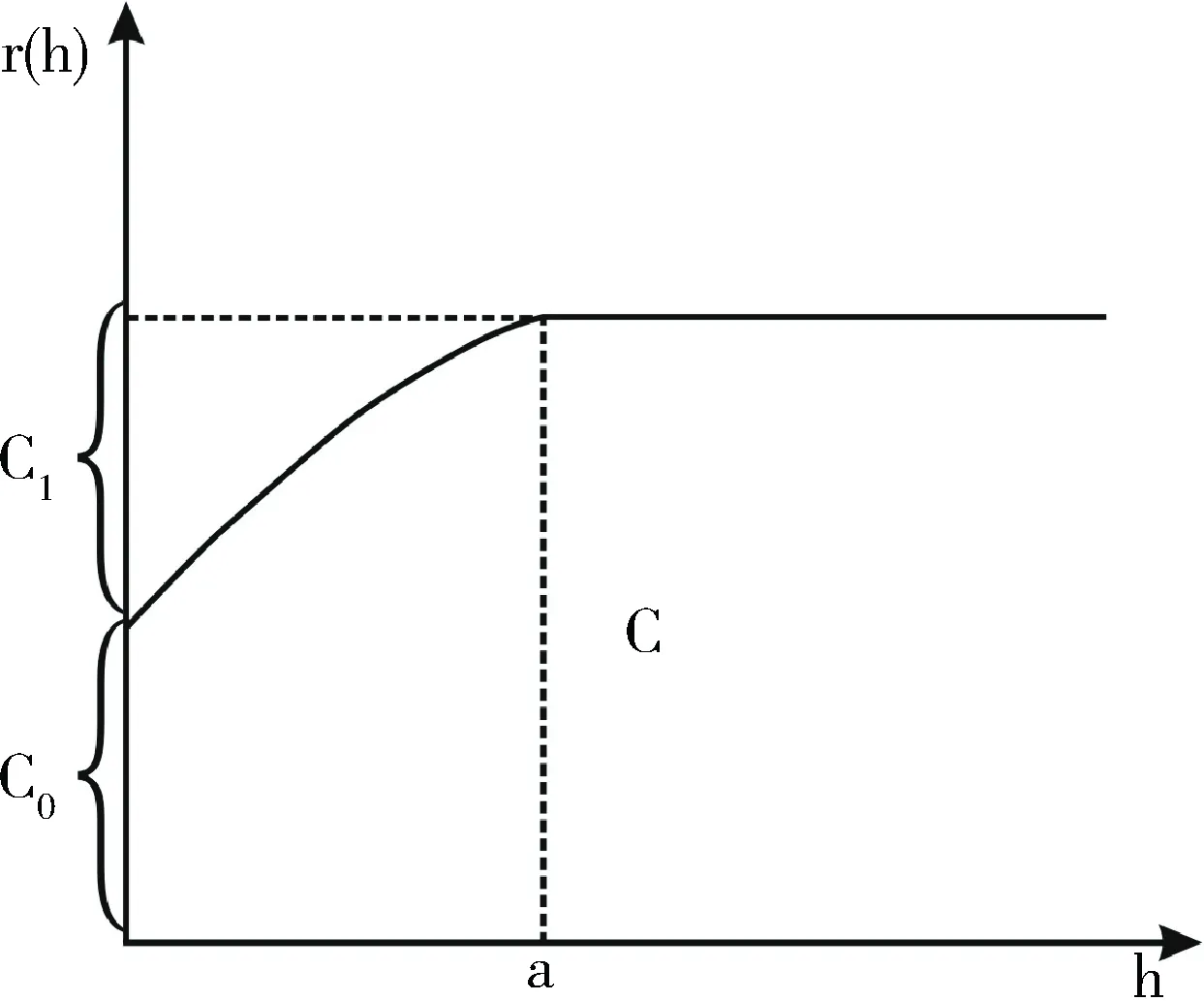
圖2 變差函數曲線圖

在實際的地質變量統計過程中，變差函數是依靠實驗變差函數r(h)的套合結構來表達區域化變量的主要特征。通過擬合實驗變差函數得到變差函數曲線圖，它是一定的變差函數值r(h)與距離h的對應圖。圖2為理想的變差函數曲線圖。圖2中的C0為塊金值，它表示h很小時兩點間的樣品的變化。變差函數如果在原點間斷，在地質統計學中被稱為“塊金效應”，塊金效應影響著區域內任意兩點間的相關性，表現為在很短的距離內有較大的空間變異性。在數學上塊金值相當于變量純隨機性部分，它可以由測量誤差引起，當它為0時，稱為無塊金效應，此時兩點間的相關性最好。在進行地質建模時，前提就是要消除塊金效應，即使C0為0[17-18]。

a為變程。當ha時，樣品間就不存在相關性。

C1為拱高；C=C0+C1，C為基臺值。代表變量在空間上的總變異性大小，即為變差函數在大于變程的值，它能反映儲層參數在某一方向變化的幅度大小，基臺值越大，參數變化幅度也越大，即各向異性越強；相反，基臺值越小，參數變化幅度也越小，即各向異性越弱。

2 不同資料擬合的變差函數對比優選分析

三維地質建模技術已成為儲層精細表征的重要手段，其目的是為準確預測儲層及其物性特征的空間展布[19-21]。目前越來越多的專家、學者致力于模擬算法及建模方法上的研究，以期提高儲層建模的精度。但是對于儲層建模中的重要環節——變差函數分析時常被人們所忽視。這可能是因為儲層參數的周期性及趨勢分布時常導致實驗變差函數空間結構不清楚，加之部分研究區或者研究層位樣本數據點少，難以擬合出有規律的理想變差函數模型。油田往往有較多的直井，由于垂向測井數據采樣率高，樣本數據點多，該方向的變差函數易于求取。但是對于平面而言，由于井少，樣本數據分布不均，擬合的變差函數常常表現為純塊金效應。針對研究區有33口水平井資料和新采集的三維地震資料，且地震資料的橫向密集采樣以及眾多水平井的多方向性，非常適合研究平面變差函數。通常情況下，開展某個地區的變差函數分析可分為以下三個步驟：第一，對變差函數理論模型進行優選；第二，在優選的變差函數理論模型的條件下，開展不同方向的變差函數擬合結果優選；第三，運用前面兩個步驟對研究區目的層各小層開展變差函數分析[15]。

2.1 水平井與直井的變差函數擬合結果對比優選分析

2.1.1 變差函數理論模型的對比優選

變差函數的擬合過程主要是對不同層位待模擬數據的帶寬、搜索半徑、搜索角度等相關參數的反復試驗修改，擬合出最佳變差函數曲線，從而求取變程值及方位[16]。CAMBARDELLA等[22]用η等于塊金值與基臺值的比來表示變量之間的相關性，認為η≤25%，說明變量間的相關性強；25%<η≤75%，說明變量存在一定的相關性；75%<η<100%,可認為變量之間存在弱相關性;當η≥100%時，則認為變量不具備相關性。據此方法，本次研究建立了三種不同類型的實驗模型，對于每一個模型，都進行了變差函數曲線分析，找出其中的差異性，作為優選模型的方法之一。同時，對于每種模型擬合結果需要從0°、45°、90°和135°等幾個大致方位進行優選，由于0°與180°、45°與225°、90°與270°、135°與315°的擬合結果一樣，因此不需要再開展方位角大于180°區域的變差函數，通過比較發現90°時的變差函數擬合結果最為理想。為討論水平井的變差函數擬合結果分析，綜合考慮水平井在某一具體層段的鉆遇數量以及鉆遇距離來開變差函數分析。圖3為塔中4東河砂巖油藏含礫砂巖段CIII_3小層方向為90°時運用水平井資料的泥質含量三種模型的實驗變差函數曲線，由于該水平井樣本數據點多，當為指數模型時，其總基臺值為1.015，塊金為0，其η=0，主變程值為778 m；球狀模型時，基臺值為1.015，塊金值為0，η=0，但是樣本數據較離散；高斯模型時，總基臺值為1.015，塊金值為0.057，η=0.08。因此，按Cambardella方法分析可知，指數模型條件下的變量相關性最好，其次為球狀模型。為了能綜合反映三種模型屬性參數的變化差異性，除了在曲線形態上進行模型的比較之外，李瓊等[23]提出了用I0=(C1+C0)/a來反映地層介質參數在某一方向的非均質性強度，認為I0值越小，非均質性越弱，反之越強。由于三種泥質含量變差函數曲線的方位角均是90°，所以比較時不受方向的影響。經計算，得到高斯模型的I0=2.857×10-3，球狀模型的I0=2×10-3，指數模型的I0=1.33×10-3，從這方面可以看出，最好的是指數模型，其在該方向上非均質性最弱，屬性變化穩定，其次是球狀模型。

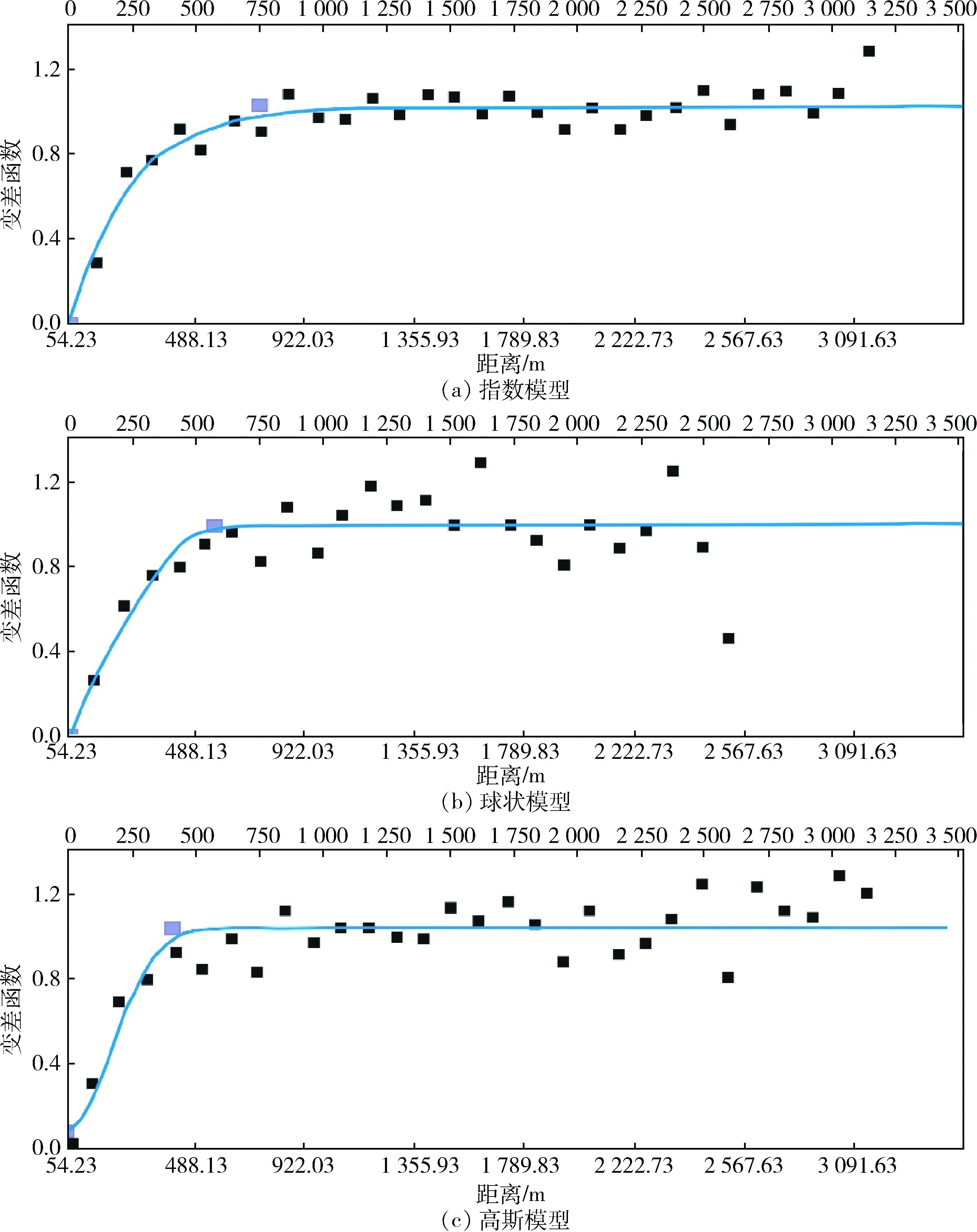
圖3 CIII_3小層不同實驗變差函數模型比較

2.1.2 水平井與直井的變差函數擬合結果對比優選

由于屬性參數在各個方向上各向異性的強弱程度不同，為了能較全面地反映儲層參數在平面上的分布規律，在前一節優選的變差函數理論模型的基礎之上，通過擬合的不同方向的變差函數曲線圖來研究平面上不同方向的非均質性，在各個方向上對每個儲層的屬性參數進行變差函數曲線分析，根據所選模型的曲線特征優選出其中的最佳變程。以研究區含礫砂巖段CIII_3小層泥質含量變差函數分析為例，目前共有9口水平井鉆遇該層。

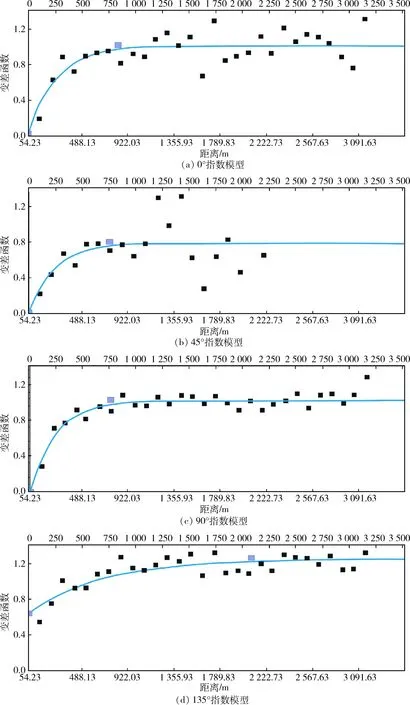
圖4 CIII_3小層不同方向的水平井實驗變差函數分析

圖4為該層泥質含量在四個不同方向所模擬出的最好的變差函數曲線，分析發現：方位角為0°和90°時，模擬結果較好。但是相比之下0°時樣本數據點空間結構性差；而45°和135°時，樣本數據已失去結構性，且在135°時的η=1，其擬合結果反映數據點已缺乏相關性。綜合考慮90°時的變程就是該層泥質含量的最佳主變程。在主變程確定之后，便可依次求得垂直該方向上的次變程及垂直變程。

對于直井而言，在相同搜索半徑、搜索步長以及帶寬等參數條件下，其泥質含量變差函數擬合結果較差，通過η、I0兩類參數的綜合比較發現，方位角在45°時，樣本數據已失去空間結構性；方位 135°時，塊金值達到了0.68，樣本數據相關性極差，方位角在0°和90°時，雖然擬合出了變差函數，但是塊金值分別為0.52和0.32，相對于水平井的擬合結果而言，其數據空間結構性相對不穩定。

因此，對于水平井資料豐富的層位，通過水平井和直井的變差函數分析結果對比發現，在優選的理論模型條件下，通過同樣參數設置下的不同方位模型優選對比發現，利用水平井資料優選的實驗變差函數模型，無論是在曲線形態方面，還是樣本數據相關性方面以及反映儲層非均質性的效果方面都遠遠好于直井擬合的變差函數結果。

2.1.3 研究區目的層位變差函數成果分析

依據水平井和直井在各小層的分布情況，采用上述方法對東河砂巖段CIII_0～CIII_12小層泥質含量參數的主變程、次變程、垂向變程都進行了求取。表1為塔中4油田東河砂巖段及含礫砂巖段CIII_0～CIII_12小層泥質含量屬性的主變程、次變程、垂向變程的數據。在對每個小層不同變差函數模型下的基臺值、塊金值、總基臺值、變程等一系列數據優選比較的基礎上，可求得塔中4油田東河砂巖油層各屬性參數的變程值，作為儲層建模的約束條件。變差函數擬合結果對比優選發現，東河砂巖段以指數模型為主，其次是球狀模型。主變程值主要在600～1 100m之間，次變程在300～650 m之間，主變程方向在45～135°范圍內，與研究區的物源方向大體一致，這在一定程度上證實了擬合結果的可靠性。

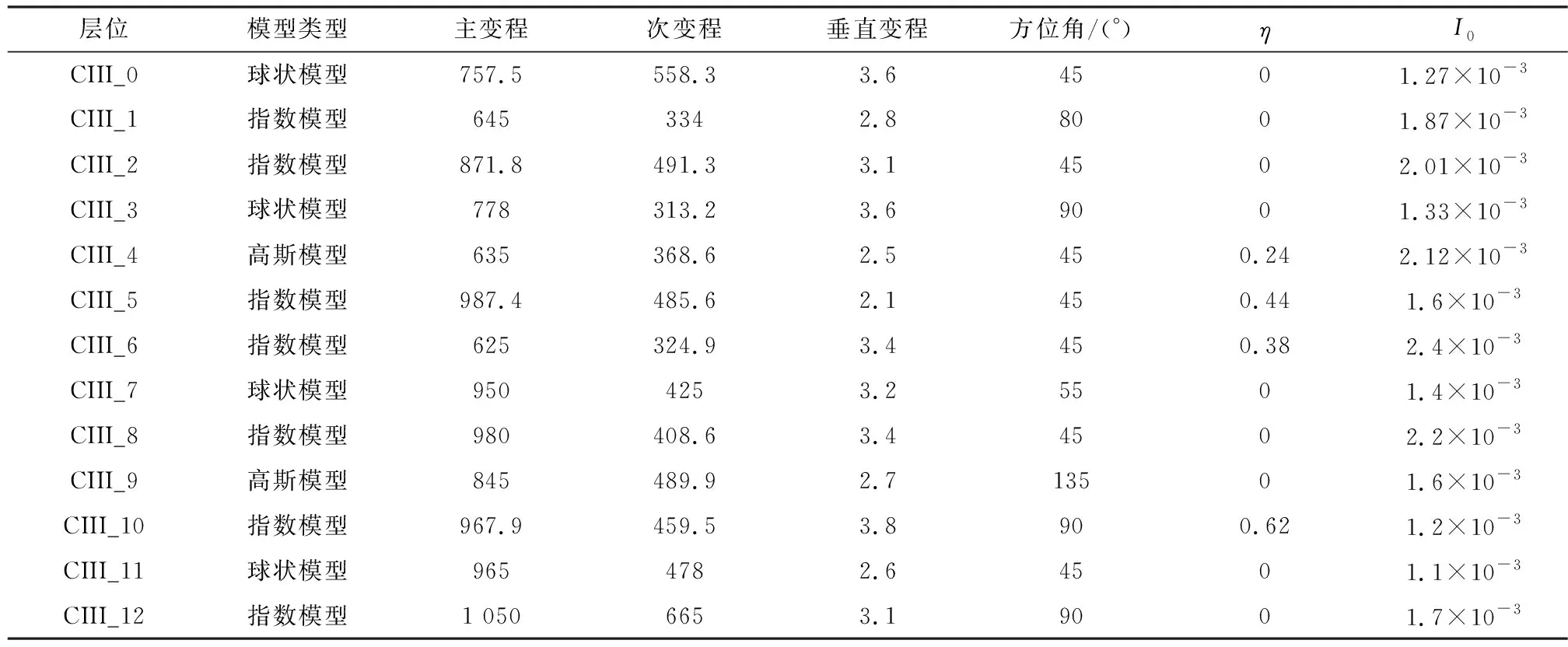
表1 泥質含量實驗變差函數分析成果表

2.2 地震資料與直井資料的變差函數擬合結果對比優選

2.2.1 少量直井條件下變差函數擬合結果的不足

目前，各大油田均存在研究目的層段底部鉆井少的情況，因此，在開展三維地質建模過程中，變差函數分析就面臨著樣本數據點不足，已有的數據點空間結構性差，難以擬合出有規律的變差函數曲線的問題。塔中石炭系東河砂巖早期沉積為一填平補齊的沉積過程，塔中4東河砂巖油藏底部CIII_13小層只在油田中部發育，平均厚度在20 m左右，共有8口井鉆遇該層位，通過不同模型下的變差函數分析發現，無論哪種模型，其樣本數據的空間結構均一樣，且不收斂，無法擬合出實驗變差函數曲線。遇到此類情況，多數建模人員是根據研究區的物源方向來給定實驗變差函數的主變程、次變程方向，依據經驗來判定該類層位的主變程值、次變程值，變差函數模型也是依據經驗選擇球狀模型。另外，也有人則是運用相鄰層位的主變程值、次變程值來建立三維地質模型，因此，所建三維地質模型也就難以接近真實的地下地質情況。

2.2.2 運用地震資料開展變差函數分析

2.2.2.1 利用地震資料求取變差函數分布圖

對于CIII_13小層，由于鉆遇層位少，樣本數點不足，擬合的變差函數均表現為純塊金效應。由于波阻抗與泥質含量存在線性相關性，且地震波阻抗屬性數據具有豐富的橫向信息，因此，可考慮運用該小層的波阻抗反演數據，通過提取該小層加權平均的波阻抗值來求取平面變差函數分布圖。利用波阻抗地震屬性計算得到的實驗變差函數平面分布圖如圖5所示，該圖橫坐標代表東、西方向，縱坐標代表南、北方向。兩個方向的基本滯后距均為20 m，每一個刻度代表1 m。平面變差函數分布圖就是以待估點為原點，縱橫坐標代表北、東方向的2維變差函數分布圖，它更能顯示出變差函數在各個方向的變化趨勢，也可看出變差函數的對稱性，同時也可把握數據的整體變化趨勢。若研究人員對所研究的地質體的空間結構有一定了解，如沉積物源、沉積相帶展布等基礎地質情況的變化趨勢，則對變差函數計算時的參數選擇是十分有利的。

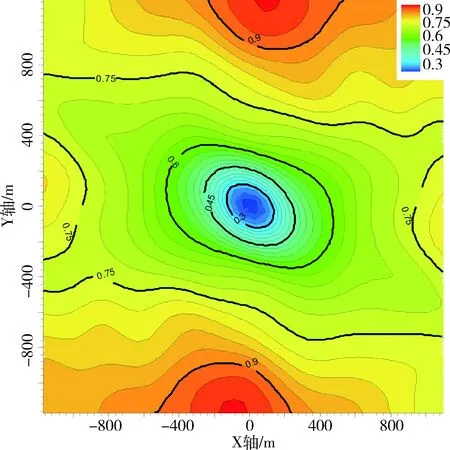
圖5 利用波阻抗求取的CIII_13小層2D變差函數分布圖

2.2.2.2 利用地震資料擬合不同方向的變差函數曲線

2D平面變差函數分布圖只能大致反映儲層非均質性的變化特征，要得到具體的主變程值、次變程值需要求取不同方向的變差函數曲線。圖6為利用波阻抗地震數據體求得的CIII_13小層不同方向變差函數曲線，擬合的基本滯后距均為20 m，擬合結果顯示，變差函數曲線的整體形態以及變化趨勢相差較大，變程值也相差甚遠，說明該層位的非均質性相對較強。從圖6中分析可知，0°、45°和90°時的變差函數曲線均表現出一定空穴效應。在135°時，擬合效果較好，為一指數模型，主變程值為1 200 m左右。此時，垂直該方向的次變程變差函數曲線則是45°時的擬合結果，其變程值為800 m左右。根據I0=(C+C0)/a對儲層非均質性的定性判斷，45°時的I0=1.25×10-3；135°時的I0=0.75×10-3，說明在135°方向的儲層非均質性比45°方向的非均質性要弱，由于研究東河砂巖底部層位發育淺水三角洲沉積，CIII_13小層水下分流河道展布方向主要為東南方向。理論上講，淺水三角洲沉積體系中，順水下分流河道方向的儲層非均質性要比切水下分流河道方向要弱，就變差函數擬合結果而言，基本上吻合了淺水三角洲沉積中儲層非均質性變化特征，這也進一步佐證了擬合結果的可靠性。

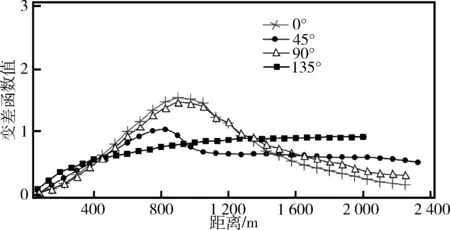
圖6 利用波阻抗地震數據求取的實驗變差函數曲線

3 優選的變差函數條件下模擬效果分析

圖7為通過水平井資料和地震資料求取的變差函數條件下的泥質含量隨機模擬結果，泥質含量是巖性的直接反映，含量的多少也間接反映了儲層砂體的發育情況以及儲層非均質性，進而也反映了泥質含量參數分布的空間結構和隨機性，其平面展布在一定程度上指示了物源的方向。目前研究認為塔中4油藏含礫砂巖段CIII_3小層的沉積微相為淺水三角洲相。CIII_3小層的河道主體發育在塔中4油藏的東南部[23]，此時，物源主要來至東、北東方向。河道分布范圍廣，延伸距離長，平面上多期河道疊置。而從本次模擬的CIII_3小層泥質含量平面等值線圖(圖7(a))可以看出，砂體呈條帶狀、東西向展布。在研究區的東南部，河道砂體較為連片分布，延伸距離遠，模擬結果與目前的地質認識吻合程度高， 進而也論證了CIII_3小層運用水平井資料開展變差函數優選的正確性與可靠性。圖7(b)為CIII_13小層運用地震資料求取變差函數條件下的泥質含量模擬結果。該層位于東河砂巖最底部，因東河砂巖早起沉積是一填平補齊的沉積過程，該層位只在塔中4油藏中部低洼地區發育，沉積體系主要為三角洲沉積，物源來自東、東南方向。前面已經述及該層共有8口直井鉆遇，如只用井資料開展變差函數模擬，因樣本數據點少，無法擬合出有規律的變差函數，進而就無法開展隨機模擬研究。而在地震資料求取的變函數條件下模擬的泥質含量結果顯示，該層位砂體呈條帶狀、北東-南西向展布。模擬的結果與早期的研究認識相符，也說明了利用地震資料求取變差函數的可靠性。對于CIII_3小層和CIII_13小層的模擬結果分析發現，其間接反映的砂體展布的方向性、砂體展布形態與前人的研究成果相吻合[24][注]據《塔中4油田周緣石炭系Ⅰ油組主力含油砂體及Ⅲ油組含礫巖段滾動開發目標優選》，2013，塔里木油田內部科研成果報告。。

4 結 論

1) 水平井具有豐富的橫向信息，可利用水平井資料開展高精度的變差函數分析，通過不同模型、不同方向的變差函數擬合結果對比發現，優選的變差函數擬合結果精度高，無塊金效應，而以直井資料擬合的變差塊金值往往較高，反映樣本數據點的相關性差。對于各油田底部層位由于鉆遇的井少，變差函數擬合存在樣本數據不足的問題，擬合結果表現為純塊金效應，則可利用地震資料開展變差函數分析，通過求取平面變差函數曲線來求得主變程值、次變程值及主變程方向。

2) 研究發現東河砂巖段泥質含量參數各層位變差函數主要以指數模型為主，其次是球狀模型。主變程值主要在600～1 100 m之間，次變程值在300～650 m之間，主變程方向在45～135°之間，通過泥質含量隨機模擬效果分析發現，在水平井和三維地震資料求取的變差函數參數條件下模擬的結果精度高，用水平井和三維地震資料求取的變差函數參數可為建立精細的三維地質模型奠定基礎。