淺談正項有界周期數列的一些性質
◎王禮斌
一、有關數列簡介以及例題詳解
1.等差數列的函數思想。

2.數列角標聯系。

3.雙數列的聯系。

4.數列的單調性。
(1)以正數開頭的遞減扥差數列的前n項和的最大值是所有非負項之和;反之,以負數作為開頭的遞減等差數列前n項和的最小值是所有非正項之和。
(2)對于等比數列{an},若 a1>0,q>1,則{an}為遞增數列;若 a1<0,q>1,則{an}為遞減數列;若 a1>0,0<q<1,則{an}為遞減數列;若a1<0,0<q<1,則{an}為遞增數列;若q<0,則{an}為擺動數列;若 q=1,則{an}為常數列。
例題1
已知數列{an},{bn},{cn}的通項公式滿足 bn=an+1-an,cn=bn+1-bn(n∈N*)
若數列{an},首項 a1=2,且滿足 cn-bn+1+3an=2n+1(n∈ N*),求數列{an}的通項公式。
分析:cn-bn+1+3an=2n+1(n∈N*),可得 bn+1-b-bn+1+3an=-2n+1,即 bn-3an=2n+1,所以 an+1=4an+2n+1,在等式 an+1=4an+2n+1,兩邊同時除以 2n+1

所以kn+1=2·2n-1=2n,即kn=2n-1.所以an=2n·kn=2n(2n-1)=4n-2n
構造數列{kn}是此題突破之處,對不熟悉的遞歸式的變形通常是為了構造新的數列,讓不熟悉的遞歸式轉化為熟悉的遞歸式。
例題2
已知數列{bn}的通項公式為bn=n.在bk和bk+1(k∈N*)之間插入3k+1個3得到一個新的數列{dn},問是否存在這樣的正整數m,使得數列{dn}的前m項的和Sm=2008,如果存在求出m的值,如果不存在請說明理由。

插入項后組成新的數列,對新數列項的構成要做具體分析,具體做法仍然是用基本量解決問題。本體在具體計算的過程中用到估算思想,希望同學們引起關注。
例題3
n2(n≥4)個正數排成n行n列



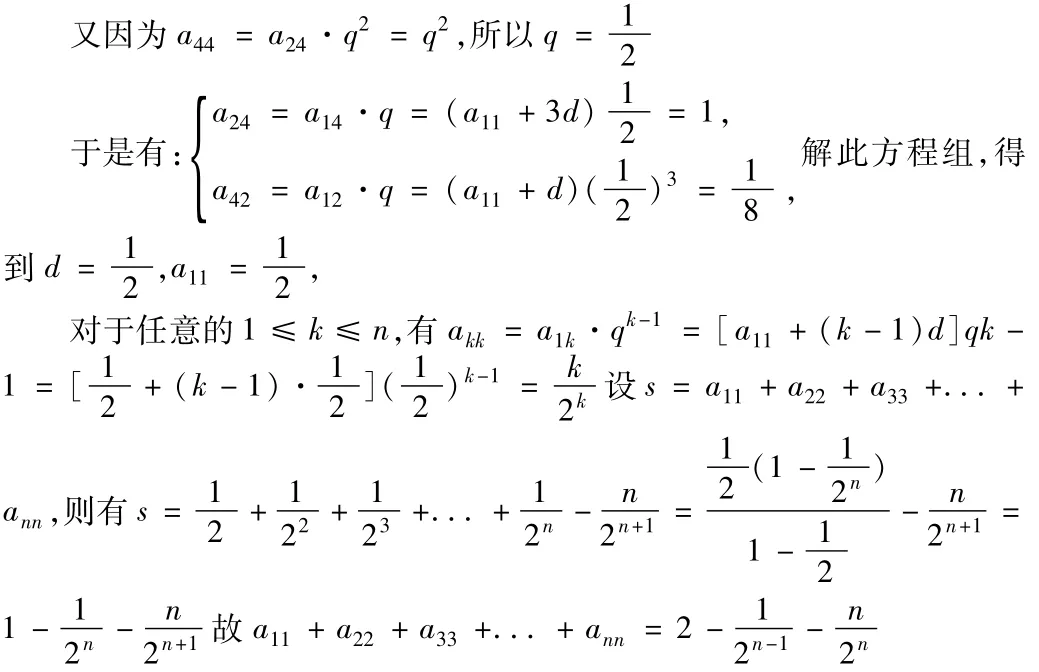
高考數學通常把考查數列的試題作為壓軸題,而且許多難度大的數列試題往往是由高中競賽數學的試題改編而來的。這道題的關鍵的盡可能多地將文字信息轉化為數學的關系式。
二、近年高考例題解析
2015年的一道數列高考題十分有特點,下面列舉和大家一起分析一下。題目如下:

(1)若a1=6,求集合M中所有元素
(2)若集合M中存在以個元素是3的倍數,證明:M的所有元素都是3的倍數.
(3)求集合M的元素最大值.
此題著重考查了遞推數列,立意新穎。第三個問題還考查了學生對數學的敏感性,同時也給其他考生留了一條出路——枚舉法。這一問題,既有難度,又無難度,是一道難得的好題。解答問題3
記Card(M)為集合M的元素個數,由于a2一定是偶數,故a3一定是4的倍數,因此,可以從a3開始討論,容易知道數列{an}中任意一項都是不大于36的正整數,并且an(n≥3)均為4的倍數,故an(n≥3)可取4(k=1,2,...,9).若a3是3的倍數,則由(2)可知,an(n≥3)只能取12,24,36,故此時 Card(M)≤5;若 a3不是3的倍數,則 an(n≥3)只能取4,8,16,20,28,32,故此時 Card(M)≤ 8;又 a1=1時,M =故Card(M)最大值為8.
由此的拓展
當 a1=6k±1時,Card(M)都可以取到最大值.當a1=9,18,27,36時,數列有極限,當a1為其他值時,存在N0∈N*,當n>N0時,數列為周期數列,因此出現以下問題:
若P為素數,a1·s∈N*,a1≤ps,

則(1)Card(M)最大值是多少?當Card(M)取到最大值時,首項是多少?
(2)若數列有極限,則首項是多少?
(3)該數列是否要么有極限,要么存在N,當n>N時,數列是不是長數列的周期數列
(4)若首項取任意值,數列都有極限,那么p,s要符合什么條件?
對于(3),當p≠2且a1=ps時,則集合M一定是無限集;所以考慮另一種推廣:an+1=p[an-(k-1)s],(k-1)s<an≤ks,其中1≤k≤p.由于分段較多,可以對PS取模,此時(3)顯然成立。其他有關問題得到結果如下:
定理的證明(1)記f(s,a1)是由s和a1確定的,集合M的元素個數,f(s)=max f(s,a1),即 f(s)是 Card(M)的最大值,令 (i,a1)=q成立.

由 ps|(an+1-pan),q|ps,t|s,
知 q|(an+1-pan),t|(an+1-pan),
由歸納法知?n∈N*,有q|an及(t,an)成立.

由{bn}的構造可知 p|b2,故由歸納得 pa+1|ba+2;
即對 ?n≥ a+2,pa+1|b成立.
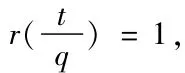
故當n≥a+2時,bn=pa+1

再由r*的最小性可知:
c1,c2,......cr*互不相同,
因 r*≤ r(t),
=a+1+r*≤a+1+r(t);
綜上可知:
f(s)=a+1+r(t),當 β=a+1,r*=r(t)時,等式成立.
即當(p,a1)=1,r*=r(t)時,Card(M)最大值 a+1+r(t)

