立體幾何中關于棱錐外接球易錯問題的分析

■河南省商丘市第一高級中學

空間幾何體與球的接切問題,本質是研究幾何體的外接球與內切球的半徑問題,是高考立體幾何選擇題或填空題的重要考查內容,不少考生對此望而生畏,也是同學們的易錯點,三棱錐的外接球考查尤為常見,錯誤率也很高,其實球的接切問題是有規律可循的。下面通過一些例題來具體講解:

一、規則幾何體外接球的常見結論

1.正方體與球。

設正方體的棱長為a。

2.長方體的外接球。

長方體各頂點可在一個球面上,故長方體存在外接球。設長方體的棱長為a,b,c,其體對角線為l,球的半徑為

3.正四面體的外接球與內切球。

正四面體作為一個規則的幾何體,它既存在外接球,也存在內切球,并且兩心合一,利用這點可順利解決球的半徑與正四面體的棱長關系。設正四面體的棱長為a,內切球的半徑為r,外接球的半徑為R,解得R=

4.直棱柱的外接球。

(1)找出底面多邊形(多見于三角形)的外心M,并求出底面外接圓的半徑。(三角形外接圓的半徑多用正弦定理求出)

(2)過底面的外心M作底面的垂線MN,MN與直棱柱中間截面的交點即為外接球的球心O。

(3)借助底面的任意頂點如A,構成直角三角形AOM,由勾股定理求出AO即為外接球的半徑。

5.正棱錐的外接球。

(1)找出底面正多邊形的中心M,并求出底面外接圓的半徑。

(2)連接底面中心與頂點P,并求出正棱錐的高PM。

(3)由正棱錐的性質得出外接球的球心在高PM上,借助底面的任意頂點如A,構成直角三角形AOM,且AO+OM=PM或者AO-OM=PM,再由勾股定理求出AO即為外接球的半徑。

6.一側面垂直于底面的三棱錐的外接球。

(1)找出底面三角形的外心M,并求出底面外接圓的半徑。

(2)找出側面三角形的外心N,過底面的外心M作底面的垂線,過側面的外心作側面的垂線,與底面垂線的交點即為外接球的球心O,且球心O到底面的距離OM即為側面的外心N到底面的距離。

(3)借助底面的任意頂點如A,構成直角三角形AOM,由勾股定理求出AO即為外接球的半徑。

二、三棱錐的外接球例題講析

例1 如圖1,三棱錐S-ABC,滿足SA⊥面ABC,AB⊥BC,SA=3,AB=2,BC=3,若O點為三棱錐S-ABC的外接球的球心,則球O的表面積為____。

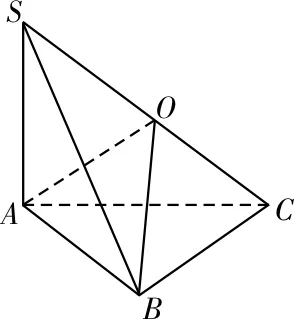
圖1

審題方法：此三棱錐四個面均為直角三角形,可借助長方體求解。

解題思路：取SC的中點為O,由直角三角形的性質可得OA=OS=OB=OC,所以O點為三棱錐S-ABC的外接球的球心,則外面積為22π。

例2 在三棱錐S-ABC中,SA=BC=3,SC=AB=2,SB=AC=3,則三棱錐S-ABC的外接球的表面積為____。

審題方法：此三棱錐的六條棱均可以看作長方體的六條面對角線。

解題思路：由已知得三棱錐的六條棱是一個長方體的六條面對角線,此棱錐的四個頂點也與長方體的其中四個頂點重合,所以此棱錐的外接球和長方體的外接球一致,由已知得長方體的三個相鄰面的面對角線為3,2,3,故外接球的半徑為11π。

例3 在三棱錐P-ABC中,PA=PB=PC=2,側棱PA與底面ABC所成的角為60°,則該三棱錐的外接球的體積為____。

審題方法：三條側棱相等的三棱錐,頂點在底面的投影為底面三角形的外心。

圖2

解題思路：如圖2,過 定 點P 作PO垂直底面于點O,外接球的球心在PO上。在直角三角形POA 中,∠PAO=60°,PA=3,所以PO=3,AO=3。設外接球的球心為H,在直角三角形HOA中,R2=HO2+AO2=(PO-R)2+AO2,計算

例4 已知三棱錐D-ABC的所有頂點都在球O的球面上,△ABC是邊長為23的正三角形,△ABD是以AB為斜邊的直角三角形,二面角C-AB-D為90°,則球O的表面積為____。

審題方法：三棱錐中由兩個面相互垂直,需找出這兩個相互垂直平面三角形的外心。

解題思路：作AB的中點M,連接CM,作CM靠近點M的三等分點O,因為面ABC⊥面ABD,所以O即為外接球的球心,AO即為外接球的半徑R=2,所以球O的表面積為16π。

變式訓練：已知三棱錐D-ABC的所有頂點都在球O的球面上,△ABC是邊長為23的正三角形,△ABD是以AB為斜邊的直角三角形,二面角C-AB-D為120°,則球

審題方法：二面角C-AB-D為120°,需從△ABC與△ABD的外心入手去尋找球心的位置。