立體幾何核心考點A卷參考答案

一、選擇題

1.C

2.C

3.D

4.B

5.C 提示:如圖1所示,在正方體ABCDA1B1C1D1中,易知AB1,AD1與底面A1B1C1D1所成的角都為45°,但AB1與AD相交,故選項A錯誤。

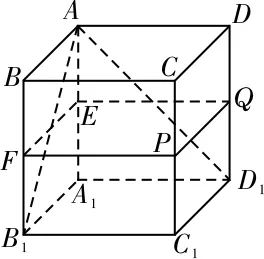
圖1

設E,F,P,Q分別是棱AA1,BB1,CC1,DD1的中點,點A,B,A1到面EFPQ的距離相等,但平面ABB1A與平面EFPQ相交,故選項B錯誤。

平面ABB1A1⊥平面ABCD。平面ADD1A1⊥平面ABCD。但平面ABB1A1與平面ADD1A1相交于A1A。故選項D錯誤。

6.D 提示:如圖2所示。

若A1A為b,CD為a,BC為c,而a,c不異面,所以①不正確。

若A1A為b,AB為a,A1B1為c,而a∥c,所以②不正確。

若A1A為b,AB為a,AD為c,而a⊥b,a⊥c,b⊥c,且a與c相交,所以④不正確。

由異面直線所成角的定義或等角定理知③正確。

圖2

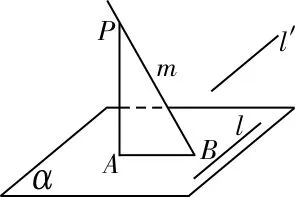
圖3

7.B 提示:如圖3所示,m是α的斜線,PA⊥α,l?α,l⊥AB,則l⊥m,α內所有與l平行的直線都垂直于m,所以A錯誤；由圖知過m有且僅有一個平面PAB與α垂直,假設有兩個平面都與α垂直,則這兩個平面的交線m應與α垂直,與條件矛盾,所以B正確；又lˊ?α,lˊ∥l,所以lˊ∥α,因為l⊥m,所以lˊ⊥m,所以C錯誤；又在平面α內取不在直線上的一點D,過D可作平面β與平面PAB平行,所以m∥β,因為平面PAB⊥α,所以平面β⊥α,所以D錯誤。

8.D

9.D

10.C

11.A

12.D

13.D

14.B 提示:如圖4所示,建立空間直角坐標系D-xyz,A(1,0,0),E(0,2,1),B(1,2,0),所以異面直線

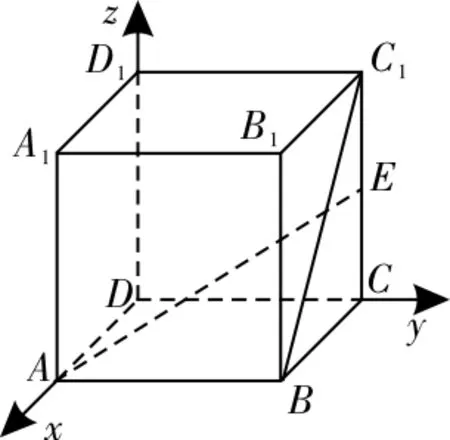
圖4

15.C 提示:取BC的中點D,在正三角形ABC中,AD⊥BC,在正三棱柱中,CC1⊥平面ABC,AD?平面ABC,所以CC1⊥AD,所以AD⊥平面BCC1B1,所以∠AC1D為AC1與平面BCC1B1所成的角,設AB=,AC1=2,所以

16.D

17.D

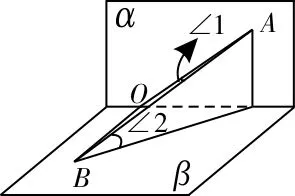
圖5

18.C 提示:如圖5所示,分別作兩條與二面角的交線垂直的直線,則∠1和∠2分別為直線AB與平面α,β所成的角。根據最小角定理:斜線和平面所成的角,是這條斜線和平面內經過斜足的直線所成的一切角中最小的角,所以∠ABO＞∠2。因為∠ABO+∠1=90°,所以∠2+∠1≤90°。

19.D

20.C 提示:如圖6所示,在正四面體P-ABC中,因為D,F為中點,所以BC∥DF,所以BC∥面PDF,故選項A成立。因為AE⊥BC,所以AE⊥DF。又BC⊥PE,所以BC⊥面PAE,DF∥BC,所以DF⊥面PAE,故選項B成立。又DF?面ABC,所以面PAE⊥面ABC,故選項D成立。由上知,不成立的是選項C。

21.B

22.C

23.A

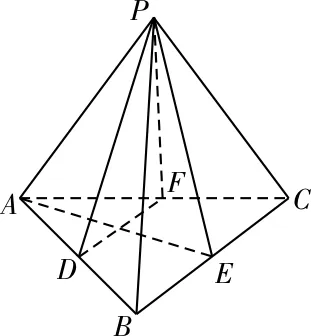
圖6

24.A 提示:如圖7所示,過點A作AC⊥l于點C,過點A作AD⊥β于點D,易證∠ACD=45°,連接BD,則∠ABD為所求線面角。設BC=a,則AC=a,AB=∠ABD=30°。

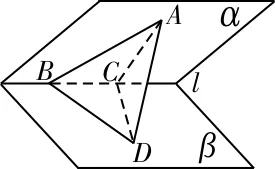
圖7

25.C

26.B 提示:①如圖8所示,由平面ABC∥平面MNP,可得AB∥平面MNP。

④如圖9所示,由AB∥CD,CD∥NP,得AB∥NP,所以AB∥平面MNP。

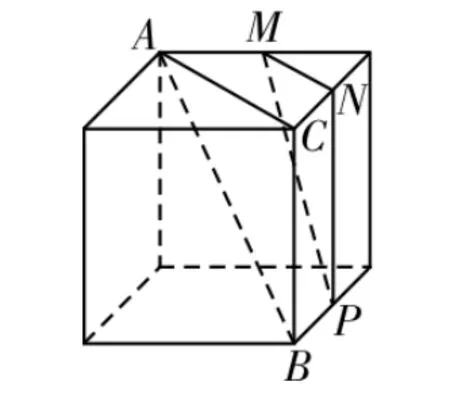
圖8

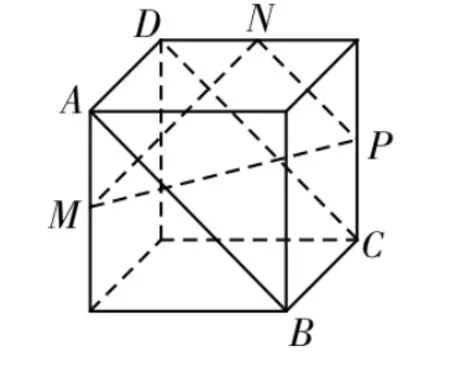
圖9

27.C 提示:正三棱錐的對棱互相垂直,即AC⊥SB。又SB∥MN,且MN⊥AM,所以SB⊥AM,從而SB⊥面SAC。所以∠BSA=90°,以S為頂點,將三棱錐補成一個正方體,故球的直徑2R=3·SA,即R=3,所以S=4πR2=36π。

28.C 提示:依題意得MN∥PQ,MN∥平面ABC。又MN?平面ACD,且平面ACD∩平面ABC=AC,因此有MN∥AC,AC∥平面MNPQ。同理,BD∥PN。又截面MNPQ是正方形,因此有AC⊥BD,直線PM與BD所成的角是45°。

二、填空題

30.4π

31.4

32.平行

33.90° 提示:取BC的中點為E,連接AE,DE,則∠AED為二面角A-BC-D的平面角,在△AED 中,AE=2,DE=2,AD=2,從而∠AED=90°。

35.①②③⑤

36.8π 提示:設外接球的半徑為r,則(2r)2=12+(3)2+22=8,故r2=2。所以S球=4πr2=8π。

37.90°

圖10

圖11

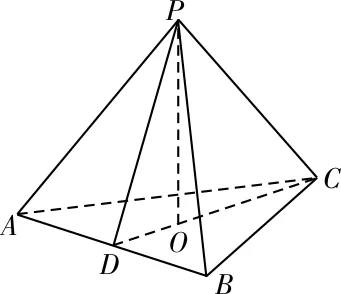
圖12

41.①②③④

43.②③④ 提示:A1B1∥AB,點E到平面ABC1D1的距離等于點B1到平面ABC1D1的距離等于,①錯誤；直線BC與平面ABC1D1所成的角就是∠CBC1=45°,②正確；空間四邊形ABCD1在正方體六個面內形成六個射影分別是正方形和直角三角形,而三角形的面積是,③正確；AE與DC1所成的角為∠EAB1,AE④正確；過點A向BD1作垂線交BD1于點F,連接CF,AC,則∠AFC即為所求二面角的平面角,因為AF=AC=

三、解答題

44.軸截面如圖13所示,設圓柱的高為h,由圓錐的平行于底面的截面性質得以h=3(1-R),V=πR2h=3πR2(1-R)≤

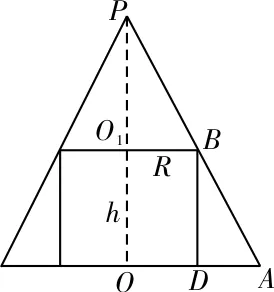
圖13

45.(1)因為底面ABCD是菱形,∠ABC=60°,所以AB=AC=AD=a。

在△SAB中,由SA2+AB2=2a2=SB2,知SA⊥AB,同理SA⊥AD。所以SA⊥平面ABCD。

(2)連接BD,設BD與AC交于點O,連接OP,點O顯然平分BD,取SP的中點為M,因為SD=3PD,所以SM=MP=PD,所以BM∥OP。因為BM?平面PAC,所以BM∥平面PAC。同理,ME∥平面PAC。因為BM∩ME=E,所以平面BME∥平面PAC。又BE?平面BME,故BE∥平面PAC。

圖14

46.(1)如圖14,過點M作ME∥CD交PD于點E,連接AE。EM。又EM∥DC∥AB,所以EMAN,所以AEMN為平行四邊形,所以MN∥AE,所以MN∥平面PAD。

(2)過點N作NQ∥AP交BP于點Q,NF⊥CB于點F,連接QF,過點N作NH⊥QF于點H,連接MH,易知QN⊥面ABCD,所以QN⊥BC。而NF⊥BC,所以BC⊥面QNF,所以BC⊥NH。而NH⊥QF,所以NH⊥平面PBC,所以∠NMH為直線MN與平面PCB所成的角,通過計算所以所以=60°。所以直線MN與平面PCB所成的角為60°。

47.(1)建立如圖15所示的空間直角坐標系,設AC∩BD=N,連接NE,則點N,E的坐標分別為又點A,M的坐標分別為NE與AM不共線,所以NE∥AM。又因為NE?平面BDE,AM?平面BDE,所以AM∥平面BDE。四邊形EMC1G是平行四邊形,所以EG∥C1M。又因為EG?平面FC1C,C1M?平面FC1C,所以EG∥平面FCC1。

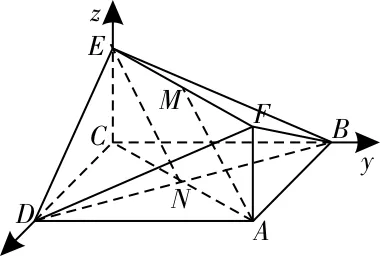
圖15

(2)在直四棱柱ABCD-A1B1C1D1中,∠BAD= ∠ADC=90°,所以 AD⊥ 平面DD1C1C。又因為EG∥平面FCC1,AB∥平面DD1C1C,B1B∥平面DD1C1C,所以

48.(1)取棱BB1的中點M,連接EM,C1M。因為E為棱AA1的中點,G為棱C1D1的中點,且AB=AD=1,CD=CC1=2,所以在直四棱柱ABCD-A1B1C1D1中,EM∥A1B1∥

(3)在平面AA1B1B內過點F作FN∥AB,交棱AA1于點N,連接DN。在直四棱柱ABCD-A1B1C1D1中,因為AB⊥平面AA1DD1,所以FN⊥平面AA1DD1,所以DN是DF在平面AA1DD1內的射影,所以當D1E⊥DF時,D1E⊥DN。

在矩形AA1DD1中,DE=D1E=2,DD1=2,所以D1E⊥DE,所以點E和點N重合,所以F是棱BB1的中點,且FE∥C1D1,所以平面EFD1即為平面EFC1D1。

在直角梯形ABCD 中,∠BAD=∠ADC=90°,AB=AD=1,CD=2,所以CB=2,CF=3。

設點C到平面EFD1的距離為d,CF與平面EFD1所成角為θ,因為DE⊥D1E,C1D1⊥DE且C1D1∩D1E=D1,所以DE⊥平面EFC1D1。又因為CD∥平面FCC1,所以d=DE=2,所以所以EFD1所成角的余弦值為

49.(1)在△BAD中,因為AB=2AD=2,∠BAD=60°,由余弦定理可得BD=3,所以AB2=AD2+BD2,所以AD⊥BD。

在直平行六面體中,GD⊥平面ADG,所以GD⊥BD。又AD∩GD=D,所以BD⊥平面ADG。

(2)以D為坐標原點,建立如圖16所示的空間直角坐標系D-xyz,因為∠BAE=∠GAD=45°,AB=2AD=2,則有A(1,0,0),B(0,3,0),G(0,0,1),E(0,3,2),C(-1,3,0)。所以=(-1,3,2),=(-1,0,1)。

圖16

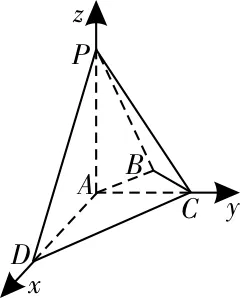
圖17

51.在折疊前的△ABC中,設BD=x(0＜x＜3),則CD=3-x。

由AD⊥BC,∠ACB=45°,知△ADC為等腰直角三角形,所以AD=CD=3-x。

由折疊前AD⊥BC知,折疊后,AD⊥DC,AD⊥BD,且BD∩DC=D,所以AD⊥平面BDC,∠BDC=90°,所以,當且僅當2x=3-x,即x=1時,取“=”。故當BD=1時,三棱錐A-BCD的體積最大。

52.(1)連接BD,四邊形ABCD是菱形,因為∠BAD=60°,所以△ABD為正三角形。

又Q為AD的中點,所以AD⊥BQ。因為PA=PD,Q為AD的中點,AD⊥PQ,又BQ∩PQ=Q,所以AD⊥平面PQB,AD?平面PAD,所以平面PQB⊥平面PAD。

(2)連接AC交BQ于點N,如圖18所示,由AQ∥BC可得△ANQ∽?平面MQB,PA?平面MQB,所以PA∥平面MQB。

圖18

(3)因為PA=PD=AD=2,Q為AD的中點,所以PQ⊥AD。

又平面PAD⊥平面ABCD,所以PQ⊥平面ABCD。

以Q為坐標原點,QA,QB,QP所在的直線為x軸,y軸,z軸,建立如圖19所示的空間直角坐標系,則各點坐標為A(1,0,0),B(0,3,0),Q(0,0,0),P(0,0,3)。

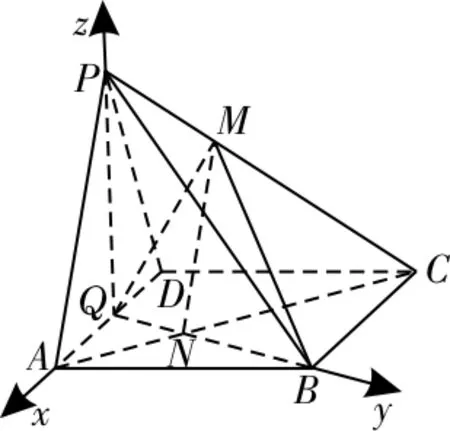
圖19

53.(1)如圖20所示,連接D1C,因為ABCDA1B1C1D1是長方體,所以A1D1∥BC且A1D1=BC。

所以四邊形A1BCD1是平行四邊形,所以A1B∥D1C。

因為A1B?平面CDD1C1,D1C?平面CDD1C1,所以A1B∥平面CDD1C1。

(2)設A1A=h,因為幾何體ABCD-

圖20

所以A1A的長為4。

(3)如圖20所示,連接D1B,設D1B的中點為O,連接OA1,OC1,OD。

因為ABCD-A1B1C1D1是長方體,所以A1D1⊥平面A1AB。

因為A1B?平面A1AB,所以A1D1⊥D1B。同理OD=OC1=

所以OA1=OD=OC1=OB。

所以經過A1,C1,B,D四點的球的球心為點O。

因為D1B2=A1D12+A1A2+AB2=22+42+22=24。

故經過A1,C1,B,D四點的球的表面積為24π。