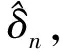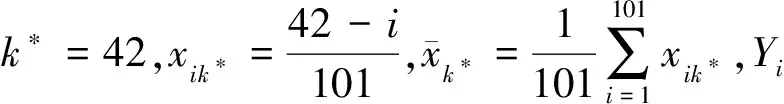長相依均值漸變模型的Ratio檢驗(yàn)
趙文芝,任肖霖
(西安工程大學(xué) 理學(xué)院,陜西 西安 710048)
在對實(shí)際的金融數(shù)據(jù)進(jìn)行分析的過程中,學(xué)者們發(fā)現(xiàn)金融市場經(jīng)常會(huì)受到一些突發(fā)事件的影響,而使得金融數(shù)據(jù)在某個(gè)時(shí)刻k后,樣本的分布或分布參數(shù)緩慢地開始變化。在對金融數(shù)據(jù)進(jìn)行建模時(shí),必須對漸變變點(diǎn)時(shí)刻進(jìn)行檢驗(yàn)。所以對均值漸變模型的變點(diǎn)檢驗(yàn)也是統(tǒng)計(jì)學(xué)的研究熱點(diǎn)。Jaru?kov(1998)[1]對隨機(jī)誤差項(xiàng)為獨(dú)立同分布序列的均值漸變模型進(jìn)行了對數(shù)似然比檢驗(yàn),得出檢驗(yàn)統(tǒng)計(jì)量的漸近分布為Gumbel分布;Hu?kov(1999)[2]對隨機(jī)誤差項(xiàng)為獨(dú)立同分布序列的均值漸變模型進(jìn)行研究,得到變點(diǎn)估計(jì)量的收斂速度及其極限分布;Hu?kov與Steinebach (2000)[3]使用CUSUM方法對漸變變點(diǎn)進(jìn)行檢驗(yàn),得到檢驗(yàn)統(tǒng)計(jì)量的極限分布;Alexander和Josef(2002)[4]研究隨機(jī)誤差項(xiàng)滿足弱不變原理的漸變隨機(jī)過程中變點(diǎn)的估計(jì),并給出變點(diǎn)估計(jì)量的收斂速度;Madurkayova(2007)[5]對隨機(jī)誤差為獨(dú)立同分布序列的均值漸變模型運(yùn)用RCUSUM函數(shù)的比率構(gòu)造Ratio統(tǒng)計(jì)量,進(jìn)行單變點(diǎn)檢驗(yàn); Steinebach和Timmermann (2011)[6]研究了具有漂移項(xiàng)的隨機(jī)過程中漸變變點(diǎn),并對其進(jìn)行序貫檢驗(yàn);Timmermann (2014)[7]對漸變變點(diǎn)進(jìn)行在線監(jiān)測,得到零假設(shè)和備擇假設(shè)下檢驗(yàn)統(tǒng)計(jì)量的極限分布;Vogt和Dette(2015)[8]研究了非參數(shù)模型中漸變變點(diǎn)估計(jì)量的漸近分布;Timmermann (2015)[9]研究了隨機(jī)誤差項(xiàng)滿足弱不變原理的漸變隨機(jī)過程,得到序貫檢驗(yàn)統(tǒng)計(jì)量的極限分布。對于長相依序列,則有Wang Lihong和Wang Jinde[10]研究了帶有長記憶性的移動(dòng)平均模型(MA)中方差突變點(diǎn)的檢測問題,在均值已知的情況下得到了未知變點(diǎn)的估計(jì)量及估計(jì)量的收斂速度,在均值未知的情況下得到原假設(shè)和備擇假設(shè)下檢驗(yàn)統(tǒng)計(jì)量的極限分布;Wang Lihong (2007)[11]給出隨機(jī)誤差為長相依序列的均值漸變變點(diǎn)的最小二乘估計(jì)量,得到該估計(jì)量的收斂速度;Wang Lihong (2008)[12]研究了長記憶MA模型中均值變點(diǎn)問題。
檢驗(yàn)漸變變點(diǎn)問題最常用的方法是累積和(CUSUM)方法,然而現(xiàn)有的CUSUM檢驗(yàn)在討論檢驗(yàn)統(tǒng)計(jì)量漸近性質(zhì)時(shí)要求原假設(shè)與備擇假設(shè)下對模型的尺度參數(shù)的估計(jì)應(yīng)該是一致的。事實(shí)上,在觀察值獨(dú)立的情況下,對模型的尺度參數(shù)的估計(jì)也并不容易,相依序列的情況就更為復(fù)雜。本文基于CUSUM函數(shù)的比率構(gòu)造了Ratio統(tǒng)計(jì)量,避免了CUSUM方法中的尺度參數(shù)估計(jì),得到了零假設(shè)和備擇假設(shè)下檢驗(yàn)統(tǒng)計(jì)量的極限分布。
1 Ratio統(tǒng)計(jì)量
考慮如下均值漸變模型:
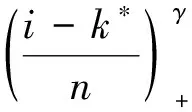
(1)
其中k*為未知變點(diǎn),a+=max(0,a),μ,δ≠0,γ∈[0,1]均為未知參數(shù)。
假設(shè)
(2)
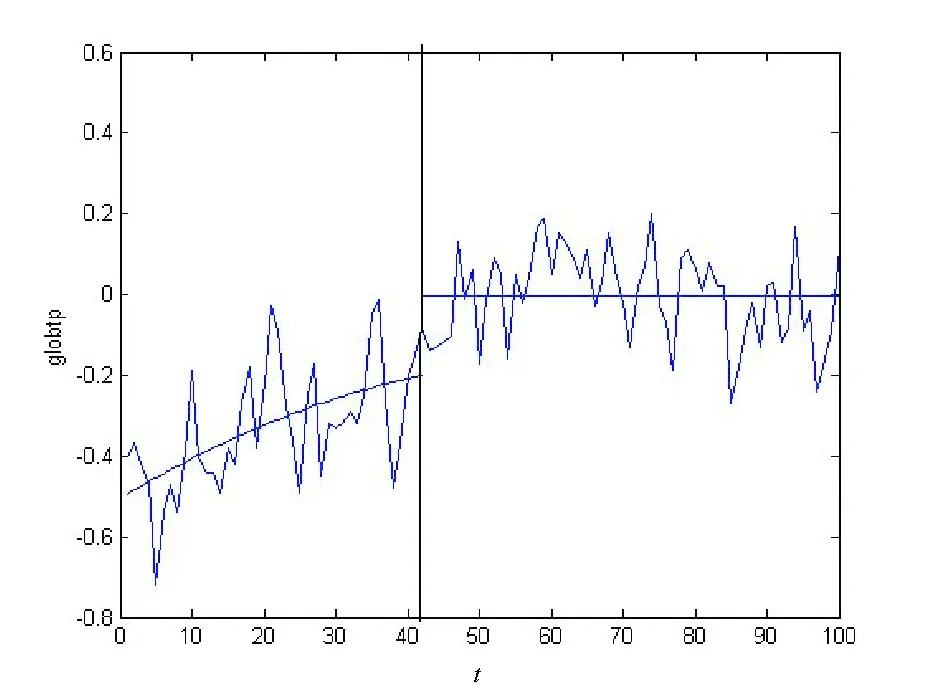
其中,{εj,-∞ 0 (3) 符號‘~’表示左邊與右邊的比率趨近于1。由文獻(xiàn)[11]可知,式(2),(3)定義的{ei}是帶有長記憶性的線性平穩(wěn)過程。 假設(shè)檢驗(yàn)如下: H0:k*=n; H1:k* 考慮Ratio檢驗(yàn)統(tǒng)計(jì)量 (4) 其中[na]表示取整,0 定理1假定Y1,…,Yn滿足模型(1)且原假設(shè)H0成立,有 (5) 證明由文獻(xiàn)[13]中式(2),(6)可得,存在一個(gè)分?jǐn)?shù)布朗運(yùn)動(dòng){Bd(y):0≤y<∞},0 (6) 其中κ是一個(gè)常數(shù)。 由文獻(xiàn)[14]可知 (7) 其中 因此,有 O((logT)1/2)a.s. (8) (9) 由文獻(xiàn)[3]中式(2.14)類似可得 因此 (10) 其中i,k=1,…,n,i 取k=[nt],i=[ns],0 Bd([nt]-m′+1)-Bd(n(t-y))dy]= (11) (12) 對于一個(gè)給定的k=[nt],結(jié)合式(10)~(12),有 (13) 類似地,可得 (14) 結(jié)合式(13),(14),可得定理結(jié)論。 定理2假設(shè)Y1,…,Yn滿足模型(1)且k*=[nt],對任意的0 n1/2|δn|→∞, (15) 則在備擇假設(shè)H1下,對a (16) 證明取k=k*,i=k*。 上式中方括號內(nèi)的表達(dá)式有非零的正極限。因此由式(15)可知當(dāng)n→∞時(shí) 定理1給出了原假設(shè)下檢驗(yàn)統(tǒng)計(jì)量的極限分布,定理2給出了備擇假設(shè)下統(tǒng)計(jì)量依概率趨于無窮,這說明當(dāng)檢驗(yàn)統(tǒng)計(jì)量的值大于臨界值時(shí)拒絕原假設(shè)。 首先采用Monte Carlo方法對檢驗(yàn)統(tǒng)計(jì)量Zn的極限分布進(jìn)行數(shù)值模擬得到臨界值。考慮到直接分析檢驗(yàn)統(tǒng)計(jì)量Zn的極限分布較難,本文采用檢驗(yàn)統(tǒng)計(jì)量的樣本分位數(shù)來近似檢驗(yàn)統(tǒng)計(jì)量極限分布的分位數(shù)。 考慮如下數(shù)據(jù)生成過程: 其中n為樣本容量,k*為變點(diǎn)位置,ei為FARIMA(0,d,0)過程。 首先驗(yàn)證d的變化對假設(shè)檢驗(yàn)的影響,取k*=n=1 000,μ=1,δ=2,γ=1,取d=0.1,0.2,0.3,0.4,對每一個(gè)d,分別對產(chǎn)生長度為1 000的FARIMA(0,d,0)序列,代入Zn可計(jì)算得一個(gè)值,重復(fù)進(jìn)行1 000次得到1 000個(gè)樣本,用該樣本的分位點(diǎn)來近似統(tǒng)計(jì)量的極限分布的分位點(diǎn),得到檢驗(yàn)統(tǒng)計(jì)量極限分布的α分位數(shù),如表1。 表1 檢驗(yàn)統(tǒng)計(jì)量極限分布的α分位數(shù)Tab.1 α quantile of cimiting distribnt 分別取樣本容量n=500,800,1 000,μ=0,δ=2,γ=1,重復(fù)進(jìn)行1 000次試驗(yàn),檢驗(yàn)水平α=0.05。模擬的經(jīng)驗(yàn)水平和經(jīng)驗(yàn)勢函數(shù)值見表2和表3。同時(shí)運(yùn)用文獻(xiàn)[11]中所給的CUSUM檢驗(yàn)的分位數(shù),模擬所得的經(jīng)驗(yàn)水平和經(jīng)驗(yàn)勢函數(shù)值見表2和表3括號中的數(shù)值。 表2 Zn的經(jīng)驗(yàn)水平Tab.2 The empirical siye of Zn 注:括號中的數(shù)據(jù)為CUSUM檢驗(yàn)法得到的經(jīng)驗(yàn)水平值。 由表2可知,當(dāng)d=0.1時(shí),樣本容量n越大,Ratio檢驗(yàn)統(tǒng)計(jì)量的檢驗(yàn)水平越接近于0.05,檢測水平失真較小。同時(shí),CUSUM檢驗(yàn)的檢驗(yàn)水平失真也較小。 表3 Zn的經(jīng)驗(yàn)勢函數(shù)值Tab.3 The emipirical power of Zn 注:括號中的數(shù)據(jù)為CUSUM檢驗(yàn)法得到的經(jīng)驗(yàn)勢函數(shù)值。 由表3可知,當(dāng)樣本容量增加時(shí),Ratio檢驗(yàn)統(tǒng)計(jì)量經(jīng)驗(yàn)勢函數(shù)值也在增加,而且樣本容量越大,經(jīng)驗(yàn)勢函數(shù)值越接近于1,檢驗(yàn)的效果越好。同時(shí),與CUSUM檢驗(yàn)法相比,Ratio檢驗(yàn)統(tǒng)計(jì)量的經(jīng)驗(yàn)勢函數(shù)值更接近1,檢驗(yàn)效果更勝一籌。 由表2和表3可知,d越大,假設(shè)檢驗(yàn)統(tǒng)計(jì)量的經(jīng)驗(yàn)水平失真越小,經(jīng)驗(yàn)勢函數(shù)值越接近于1。 然后,驗(yàn)證γ的變化對假設(shè)檢驗(yàn)的影響。分別取樣本容量n=500,800,1 000,μ=0,δ=2,d=0.1,γ=0,0.25,0.5,0.75,1,重復(fù)進(jìn)行1 000次試驗(yàn),檢驗(yàn)水平α=0.05。模擬的經(jīng)驗(yàn)水平和經(jīng)驗(yàn)勢函數(shù)值見表4和表5。同時(shí)運(yùn)用文獻(xiàn)[11]中所給的CUSUM檢驗(yàn)的分位數(shù),模擬所得的經(jīng)驗(yàn)水平和經(jīng)驗(yàn)勢函數(shù)值見表4和表5括號中的數(shù)值。 表4 Zn的經(jīng)驗(yàn)水平Tab.4 The empirical siye of Zn 注:括號中的數(shù)據(jù)為CUSUM檢驗(yàn)法得到的經(jīng)驗(yàn)水平值。 由表4可知,當(dāng)γ=1時(shí),樣本容量n越大,Ratio檢驗(yàn)統(tǒng)計(jì)量的檢驗(yàn)水平越接近于0.05,檢測水平失真較小。同時(shí),CUSUM檢驗(yàn)的檢驗(yàn)水平失真也較小。 表5 Zn的經(jīng)驗(yàn)勢函數(shù)值Tab.5 The empirical power of Zn 注:括號中的數(shù)據(jù)為CUSUM檢驗(yàn)法得到的經(jīng)驗(yàn)勢函數(shù)值。 由表5可知,當(dāng)樣本容量增加時(shí),Ratio檢驗(yàn)統(tǒng)計(jì)量經(jīng)驗(yàn)勢函數(shù)值也在增加,而且樣本容量越大,經(jīng)驗(yàn)勢函數(shù)值越接近于1,檢驗(yàn)的效果越好。同時(shí),與CUSUM檢驗(yàn)法相比,Ratio檢驗(yàn)統(tǒng)計(jì)量的經(jīng)驗(yàn)勢函數(shù)值更接近1,檢驗(yàn)效果更勝一籌。 實(shí)例 為驗(yàn)證Ratio檢驗(yàn)法的有效性,以全球平均溫度為例,分析從1880年到1980年的101個(gè)歷史數(shù)據(jù)(數(shù)據(jù)來自http://www.datatang.com/data/3490),首先得到原始數(shù)據(jù)的時(shí)序圖,如圖1所示。 圖1 全球平均溫度時(shí)序圖Fig.1 Global average temperature sequence diagram 從圖1觀察發(fā)現(xiàn),所選時(shí)間段間的數(shù)據(jù)呈現(xiàn)漸變的趨勢,可能存在變點(diǎn)。用本文的Ratio檢驗(yàn)法,假設(shè)檢驗(yàn)如下: H0:k*=101; H1:k*<101,δ≠0。 將所選數(shù)據(jù)帶入檢驗(yàn)統(tǒng)計(jì)量Zn中,計(jì)算得到在α=0.05檢驗(yàn)水平下,Ratio檢驗(yàn)統(tǒng)計(jì)量Zn=1.198,大于d=0.1,μ=0,δ=2,γ=1時(shí)對應(yīng)的臨界值0.305 7,因此拒絕原假設(shè),也就是說所選時(shí)間段間的數(shù)據(jù)存在變點(diǎn)。 記時(shí)間1880年為t=1,1881年為t=2,一直到1980年為t=101,運(yùn)用最小二乘法估計(jì)出變點(diǎn)發(fā)生在t=42,即1922年。從圖1可以看出,1922年后全球平均溫度呈上升趨勢,查閱相關(guān)資料,猜測可能是工業(yè)革命以后,人類大量使用化石燃料,制造了大量二氧化碳等溫室氣體所造成的溫室效應(yīng)引起了全球平均氣溫的波動(dòng)。 Yi=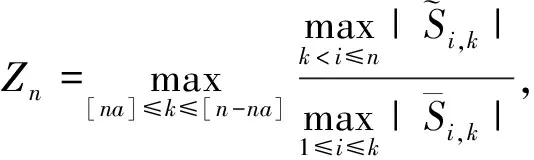
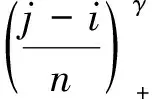
2 統(tǒng)計(jì)量的極限分布
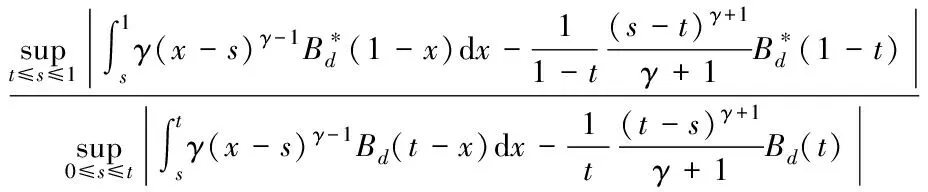
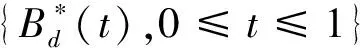

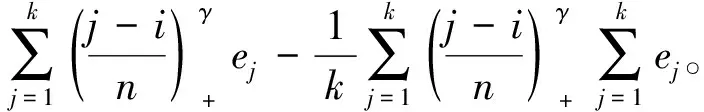
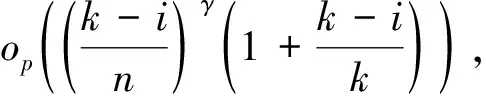
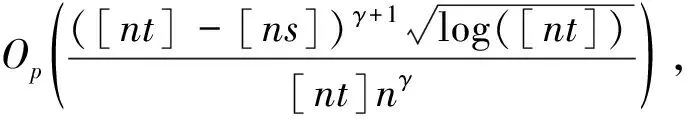
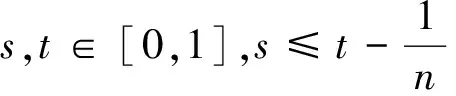
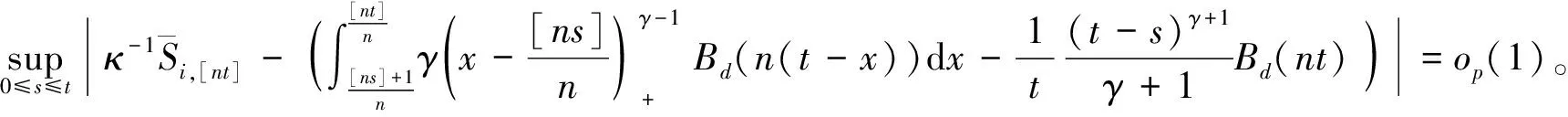
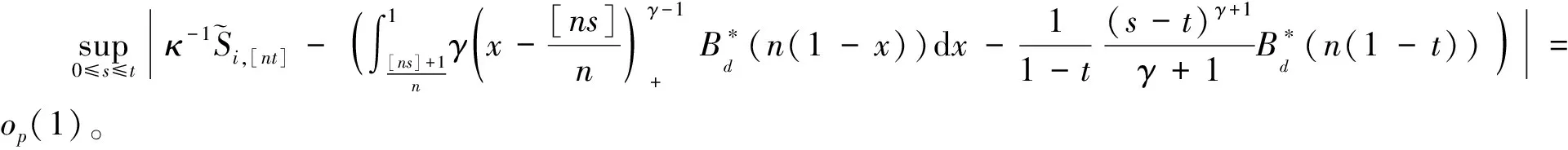
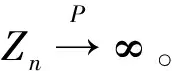
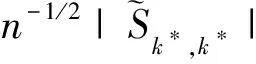
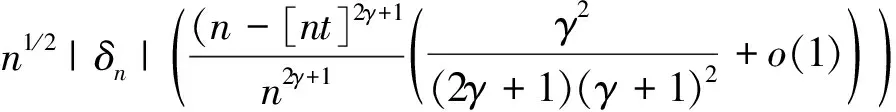
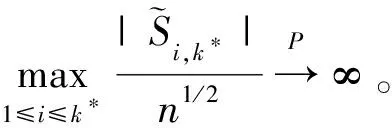
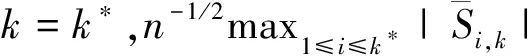
3 數(shù)值模擬及實(shí)例分析
3.1 數(shù)值模擬





3.2 實(shí)例分析