基于博弈論的教育體制和中學生能力關系的納什均衡模型探究

趙義瀟

（陜西師范大學附屬中學 陜西 西安 710061）

1 序論

1.1 背景問題

目前來說，教育體系已經日趨完善，各個地方也都有針對不足的具體措施，但仍存在的問題是當前中學生的綜合能力培養方面，在師生關系，教育減負等多方面仍存在著不足，適時找出解決方案，有利于教育事業的穩步進行，更有利于未來創新型人才的培養與發展。

1.2 本文工作

本文想從博弈論的視角，從模擬師生關系，教育減負，競爭關系和高考制度這四方面入手，探究教育體制中影響中學生能力的重要因素，并致力于得出有價值的解決方案。本文將學生和老師、家長等作為博弈雙方，使用博弈論中的納什均衡模型，將博弈雙方的作用量化，放在納什均衡模型中進行分析，并最終得到納什解，通過分析均衡點來解釋博弈雙方應該采取的方案和策略。

2 模型介紹

2.1 博弈論介紹

博弈論，英文稱“gametheory”，也稱對策論。原是一種數學的運籌學方法，通過不同的角度，博弈論大致有以下幾種分類方法：

a）非合作博弈和合作博弈

根據參與者的集合類型可以分為非合作博弈和合作博弈兩種類型。以單個參與人可能行動的集合為基本元素的稱為非合作博弈，以參與人群的可能聯合行動的集合為基本元素稱為合作博弈。

b）戰略博弈和擴展博弈

每個參與人選擇且僅選擇一次行動計劃且所有參與人的決策同時做出，也就是說每個參與人并不知道其他參與人的行動計劃，這樣的博弈叫做戰略博弈。

c）完全信息博弈和不完全信息博弈

根據博弈時參與人對整個博弈的了解程度可以分為完全信息博弈和不完全信息博弈兩種類型。其中完全信息博弈是說每個參與人都清楚其他參與人的行動，比如下棋就屬于完全信息博弈。而不完全信息博弈則是說參與人并不能夠直觀的了解到有關博弈的所有情況，著名的囚徒困境模型就屬于不完全信息博弈。

2.2 納什均衡

所謂納什均衡，是指一個博弈中每個參與者在其他人不改變策略的情況下，都無法通過改變自己的策略來獲得更多收益的局面。換句話說就是在該策略組合中，任何參與人單獨改變策略都不會得到好處，則稱該策略組合為納什均衡。

3 研究方向

3.1 師生關系和學生能力

3.1.1 問題分析 學生與老師打交道已經是不可避免的事實，而兩者的相處方式如何，自然會在某種程度上影響到一個學生的心情和狀態。單就教師而言，負責程度不同，所導致的與學生相處的方式就會大相庭徑：教師越負責，通常情況下學生越聽話，學習成績提升更有效率，但該種方式會導致教師花費大量時間精力來掌控學生的狀態，一昧追求學習成果，反而會導致師生之間爆發矛盾沖突，致使教師所花費的時間精力與達成的效果并不成正比，甚至可能產生反效果；教師越不負責任，矛盾沖突減少，相處關系比較緩和，對學生的管理程度較松散，學生提升學習能力主要依靠道德自覺，但建立在道德自覺之上的能力并不牢固，學生本身的偷懶習性也有可能因此觸發，故學習成果也會因教師的不負責任而降低。

3.1.2 模型引入 針對問題合理簡化后，對于教師而言有兩種選擇：負責或者不負責；學生也有兩種選擇：配合或不配合。若教師負責而學生配合，則教師輕松且學生能力得到有效提升；若教師負責而學生不配合，則師生矛盾激化，教師需要付出的代價相對較大且學生能力提升低；若教師不負責任而學生配合，則教師輕松，但學生會因教師的不嚴謹態度無法有效提升自身能力；若教師不負責而學生不配合，則教師需要付出的代價不多，但學生同樣無法有效提升自身能力。

若兩方都為了獲取自己的最大收益，那么根據囚徒困境模型的分析來說，最終的納什解為雙方都不采取積極行動的非合作點上。

3.2.3 結論解釋 納什解最終落在非合作點上，對各自來說都達到了自己的最大獲利點，但卻并沒有獲得整體的最大利益。為了解決這種局面，對教師來說，應當樹立良好的教育態度，也必須增強責任意識，培養奉獻精神；對學生來說，應當努力配合老師，積極完成學業，為自己未來的發展樹立長遠的眼光。唯有師生攜手共進，才能圓滿完成教育任務。

3.2 教育減負和學生能力

3.2.1 問題分析 教育減負政策出臺已經有不短的時間了，然而落實情況卻不容樂觀，關鍵性原因就是近年來校外補課機構的不斷興起，使很多家長意識到不能讓孩子輸在起跑線上。在并未與孩子達成共識之前，就為孩子增添課業負擔，導致現階段中學生的壓力很大。

從家長的角度來看，每個家長都擁有兩種選擇：減負或不減負。但根據現實情況，假設有A、B兩學生家長，互不知道對方子女的學習狀態，那么會做出何種決策？

3.2.2 模型引入 這需要根據A,B雙方的決策得到結論：若A,B均減負，則機會均等，且兩人壓力都不重；若一人減負而另一人不減負，則不減負的學生壓力更大，但同時機會更多，獲益更多；若A,B均不減負，兩人壓力都重，但機會也相等。具體矩陣圖如下：

家長A/B 減負 不減負減負 （x1,y1） （x2,y2）不減負 （x3,y3） （x4,y4）

1）x1=10, y1=10

2）x2=9, y2=6

3）x3=6, y3=9

4）x4=6, y4=6

我們根據實際的調查和相關的研究給出了以上數值。根據矩陣圖，不管另一方怎么選擇，不減負都是自方最大化效益的決策選擇。

3.2.3 結論解釋

該結論有效地解釋了教育減負難以落實的原因，但教育發展不能單純只靠增負，因為這樣只會導致學習成績的暫時性提高，似乎是短時間內占據了優勢，卻失去了學生未來“可持續”發展的熱情和動力，顯然不是一個好事情。

而想要讓教育達到更高的水平，個體水平對解決問題的能量已經很小了，就需要政府或教育局發布更有力的政策方針，主要針對教育減負的問題做出可行性強的改變。對一個家庭來說，要著手學生的心理輔導，既要適當增壓適應當前潮流，也要在學習之余做好孩子課外各方面的能力，讓學生多方面能力得到提升。

3.3 競爭關系和學生能力

3.3.1 問題分析

對現階段中學生來說，目前最重要的目的就是考試成績，這也是反應一個學生能力的指標之一，但由于同學之間存在競爭關系，故大多數學生的排名不可能總是一成不變的，而成績是由一段時間的學習狀態和考試時的心理壓力等多方面因素導致的，其中自然也就包括自己之前的成績影響。

部分同學會因為某次考試的好成績生出驕傲的情緒，這種情緒有一定幾率導致思想上的松懈，從而將會引起下一次考試成績的退步，被其他同學趕超。每位同學有三種策略：保持原樣、向前追趕、驕傲自滿，關于成績的收益如下：

學生A/B 保持原樣 向前追趕 不再努力保持原樣 （x1,y1） （x2,y2） （x3,y3）向前追趕 （x4,y4） （x5,y5） （x6,y6）不再努力 （x7,y7） （x8,y8） （x9, y9）

關于心理滿足感的收益

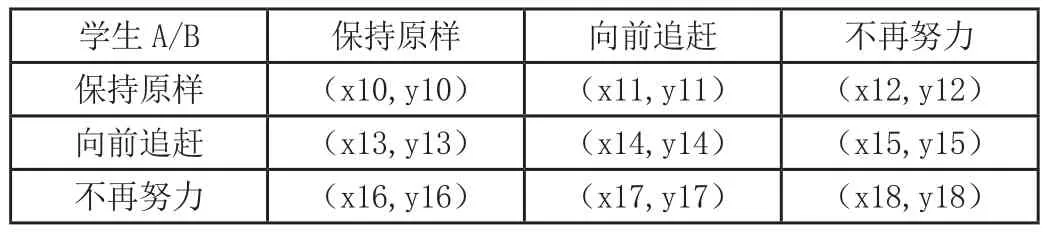
學生A/B 保持原樣 向前追趕 不再努力保持原樣 （x10,y10） （x11,y11） （x12,y12）向前追趕 （x13,y13） （x14,y14） （x15,y15）不再努力 （x16,y16） （x17,y17） （x18,y18）

綜合收益

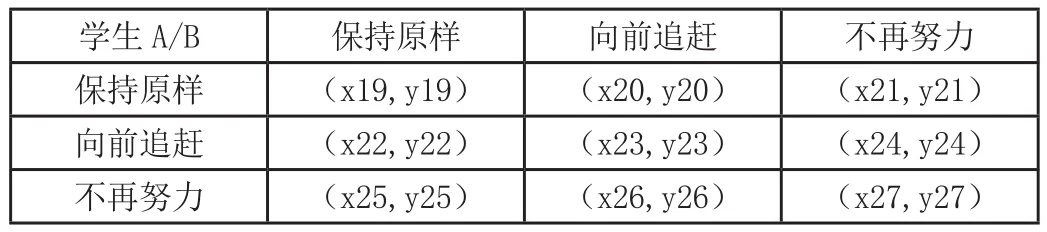
學生A/B 保持原樣 向前追趕 不再努力保持原樣 （x19,y19） （x20,y20） （x21,y21）向前追趕 （x22,y22） （x23,y23） （x24,y24）不再努力 （x25,y25） （x26,y26） （x27,y27）

我們首先將眾多學生的競爭簡化成兩個學生之間的競爭關系，暫記為學生A和學生B（A的成績略高于B），且如果A在某次考試后產生了驕傲的情緒，那么B就會在下一次的考試中超過A，出于不想被超過，A自然是不愿意產生驕傲的情緒。

1）x1=1, y1=0

2）x2=-1, y3=7

3）x3=0, y3=-1

4）x4=7, y4=-1

5）x5=10, y5=10

6）x6=5, y6=-5

7）x7=-1, y7=0

8）x8=-5, y8=5

9）x9=-2, y9=-2

10）x10=3, y10=3

11）x11=1, y11=5

12）x12=5, y12=1

13）x13=5, y13=1

14）x14=1, y14=5

15）x15=8, y15=-1

16）x16=1, y16=5

17）x17=-1, y17=8

18）x18=10, y18=10

19）x19=3, y19=3

20）x20=0, y20=12

21）x21=5, y21=0

22）x22=12, y22=0

23）x23=11, y23=11

24）x24=13, y24=-6

25）x25=0, y25=5

26）x26=-6, y26=13

27）x27=8, y27=8

我們根據實際的調查和相關的研究給出了以上數值。

3.3.2 模型引入 我們首先將眾多學生的競爭簡化成兩個學生之間的競爭關系，暫記為學生A和學生B（A的成績略高于B），且如果A在某次考試后產生了驕傲的情緒，那么B就會在下一次的考試中超過A，出于不想被超過，A自然是不愿意產生驕傲的情緒。

由此類推到數量更多的餓獅博弈鏈中，學生A之后還有許多像B一樣的學生，所以同學根本不敢產生驕傲的情緒。該模型與餓獅博弈不同之處在于，不存在沒有受到來自較弱同學的壓力的個體，而是每一個追求上進的理性個體，都會受到像餓獅博弈中來自許多同學的“威脅”。

4 結論

4.1 本文總結

本文單就做了總結，意在為中學生提供明確清晰的目標和選擇，使用了納什均衡的部分模型，適當簡化現實問題并進行分析，根據博弈論總結得出中學生的學習能力與四個不同方面因素的影響，有效利用此結論可以為學生日后的發展打好基礎，但本文不足之處在于沒有考慮到現實生活的各種情況，所以得出的結論未必完全適用于所有情況。

其次，博弈論模型的基本假定認為所有人的能力和理性均一致，不過現實情況往往不然，畢竟社會生活中不是所有人都能夠始終保持理性，因為受到知識水平、時間精力、經濟發展狀況、價值取向、感性判斷等因素的限制，會對博弈者的行為產生一定程度的影響，導致最終得出的解不總是完全正確的。現代博弈理論正在引入有限理性來優化結果，這也是博弈論研究中的一大重要方向，說明了博弈論的理論研究也正在處于不斷完善、不斷發展的過程中。

4.2 未來展望

針對以上情況，以后會多考慮這方面的限制情況，從不同角度更加全面地進行分析，同時也會適當通過考慮有限理性存在的情況，對整個問題的掌握會更加深入，得出的結論也會更加到位。同時也會盡可能引入不完全理性的分析方案，使得這些模型能夠更好地適應社會生活中的諸多問題，從而能有效地解決問題。