破冰結構角度對整冰失效模式的影響分析

白旭 周利 陶冶

(江蘇科技大學船舶與海洋工程學院, 江蘇 鎮江 212003)

提要 破冰船破冰過程中整冰的失效模式對于冰載荷的估算十分重要。本文基于力學方法分析了破冰船破冰過程中破冰結構與整冰的相互作用, 得到了影響冰體失效的冰力分量與破冰結構參數的表達關系, 進而確認冰摩擦系數以及坡度角與冰體失效模式的關系。依據北極海冰的摩擦系數范圍, 指出當破冰船破冰結構坡度角小于 70°時, 冰體發生彎曲破壞, 當坡度角處于 70°—82°時, 冰體同時發生彎曲和擠壓失效, 當坡度角大于82°時, 冰體僅發生擠壓失效,同時給出了不同失效模式下冰力的計算方法。

0 引言

近十幾年來, 隨著全球氣候變暖, 北極冰層逐年融化, 各國對連接歐洲、東亞和北美的北極航線的探索不斷深入; 與此同時, 對北極地區油氣和礦產資源的關注不斷升溫。極地冰區的通航和科學考察、資源勘探需依靠破冰船開辟航道,破冰航行。因此, 準確模擬破冰船的破冰過程具有重要的理論和現實意義。

當前, 國內外已經開展了大量的關于破冰過程的研究。Riska等[1-2]提出了一些半理論半經驗的預報模型, 為早期的破冰船設計提供了有效的方法。將破冰過程劃分為四個部分: 冰碎、旋轉、滑移以及清除。Wang[3]提出了一種運動的海冰與固定錐形結構相互作用的算法, 并對海冰的破壞過程進行了模擬。Su等[4]對破冰船破冰過程的冰載荷進行了研究, 模擬了整個破冰過程。Nguyen等[5]利用這種冰破碎模式來模擬冰船之間的相互作用。Valanto[6]將冰船相互作用過程分為四個階段: 破冰、旋轉、滑行和清除。他利用三維數值模型來模擬水線面上破冰過程, 碎冰對船舶的阻力根據 Lindqvist的經驗公式來計算。Sawamura等[7]也模擬了浮冰在高頻力的作用下的動態響應,獲得了浮冰的彎曲性能,提出了一套連續接觸程序來計算冰力。基于商業軟件PhysX, Lubbad和L?set[8]模擬了船與冰相互作用的物理過程。加拿大學者 Sayed和 Barker[9]基于混合拉格朗日方程的質點網格法模擬了冰塊與一個錨泊平臺之間的相互作用。Zhou等[10-11]利用二維的數值方法來模擬漂浮平整冰與錨泊結構物之間的相互作用。水線面處破冰的過程用幾何的方法來模擬,冰的旋轉和滑行過程中的沖擊力用半經驗公式來計算。

國內學者也開展過相關研究。天津大學的Huang等[12]在冰池中對一艘運輸船開展了冰阻力模型試驗研究, 利用單自由度測力儀測量船模拖航時不同速度下的冰阻力。翟帥帥等[13]模擬了破冰船在直航時的連續破冰模式, 得到了破冰船破冰過程中的冰載荷時歷曲線, 并分析了破冰參數對破冰形狀以及平均冰阻力的影響。何菲菲[14]利用彈性力學理論對冰載荷進行了求解。王鈺涵等[15]針對破冰船在直航情況下的連續破冰模式運用數值方法進行了研究, 得到了破冰過程中的冰載荷時歷曲線。桂大偉等[16]對“雪龍”號破冰船的沖撞式破冰模式進行了研究。

以上研究在破冰載荷的計算過程中僅考慮了冰體的彎曲失效, 對于具有大坡度結構的破冰船來說, 其破冰過程中存在的擠壓失效方面的研究仍是空白。如果仍采用傳統的彎曲失效假設來計算冰層對大坡度結構物的作用, 將出現在垂直于冰層方向的分力過小甚至為負數的情況, 導致冰層局部無法斷裂, 局部冰載荷隨時間增大而無限變大等不合理現象, 因此需要對現有數值模擬方法開展進一步的完善工作。本文基于模型試驗以及實船試驗時觀測到的破冰船破冰時的物理過程,對船體與冰層相互作用的過程進行分析, 提出了不同的冰失效模式, 并給出了破冰結構物不同傾角下冰載荷的計算模型, 從而可以用來模擬大坡度結構的連續破冰過程。

1 破冰結構與整冰作用的力學分析

冰、水與結構物相互作用的過程是十分復雜的, 在此過程中, 相應的物理現象很難用數值的方法進行再現。因此, 一般需要假定冰的流速相對較低, 進而可以忽略水的抨擊作用。

在破冰的過程中, 整冰與船體破冰結構的接觸如圖1所示。假設其接觸表面是平的, 接觸面積可由接觸長度和接觸深度來確定。整冰破碎后產生的浮冰的幾何形狀是不確定的, 一般可將其假設為扇形, 破冰扇形角度為 θ, 破冰半徑根據文獻[3]給出的表達式為

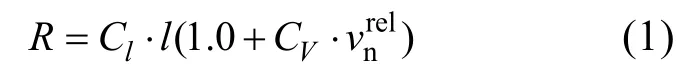
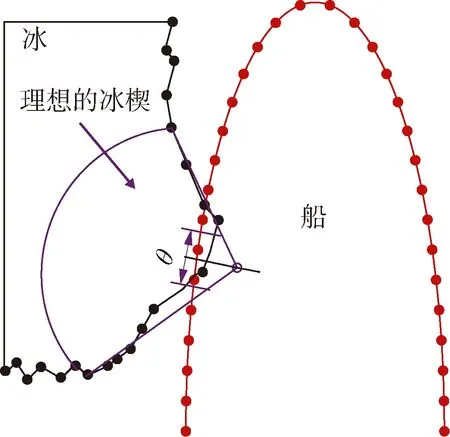
圖1 整冰與破冰結構接觸示意圖Fig.1.Schematic diagram of structure contact with ice

式中，E為彈性模量，hi為冰厚，v為泊松比，ρw為海水密度，g為重力加速度。

破冰過程的冰載荷假設為均勻的, 等效為有效的抗壓強度。隨著冰與結構接觸面積的增加,壓碎力逐漸減小。在彎曲破壞前, 擠壓的冰力產生于擠壓的表面, 并垂直于擠壓表面, 對接觸表面上產生的局部冰壓碎力可以表示為

式中, Ac為接觸面積, σc為海冰擠壓強度。

船體與冰的相對速度 vrel和力的分量如圖2所示,和分別為 vrel沿船體接觸點法向和切向方向的分量, 而和分別為垂直面內沿船體接觸面和垂直于接觸面方向的分量, fh和 fv分別為水平和垂直方向上的摩擦力分量, 垂直于船體表面的擠壓冰力 Fcr與摩擦力 fv的合力可以分解為水平分量Fh和垂直分量Fv, 由于冰體在彎曲破壞前沒有垂向位移, 所以 fh與相對速度分量成正比, 而 fv與相對速度分量成反比, 根據文獻[4]可以表達為

式中, μi為船體與海冰之間的摩擦系數。

2 破冰結構角度與整冰失效

整冰在破冰結構的作用下若發生彎曲失效,如圖1所示, 將形成一個開角為θ的冰楔, 在冰楔的頂端受到垂直的載荷, 依據文獻[17]對海冰承載能力的估算式為

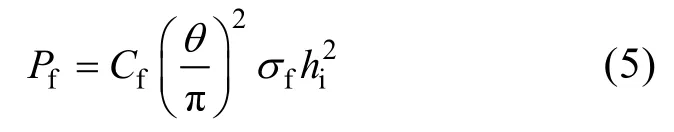
式中, σf為海冰的彎曲強度, hi為海冰厚度, Cf為經驗參數。當冰破碎和摩擦力的垂直分量大于Pf時, 冰楔將從彎曲形成的冰邊緣裂開并折斷, 彎曲失效發生。

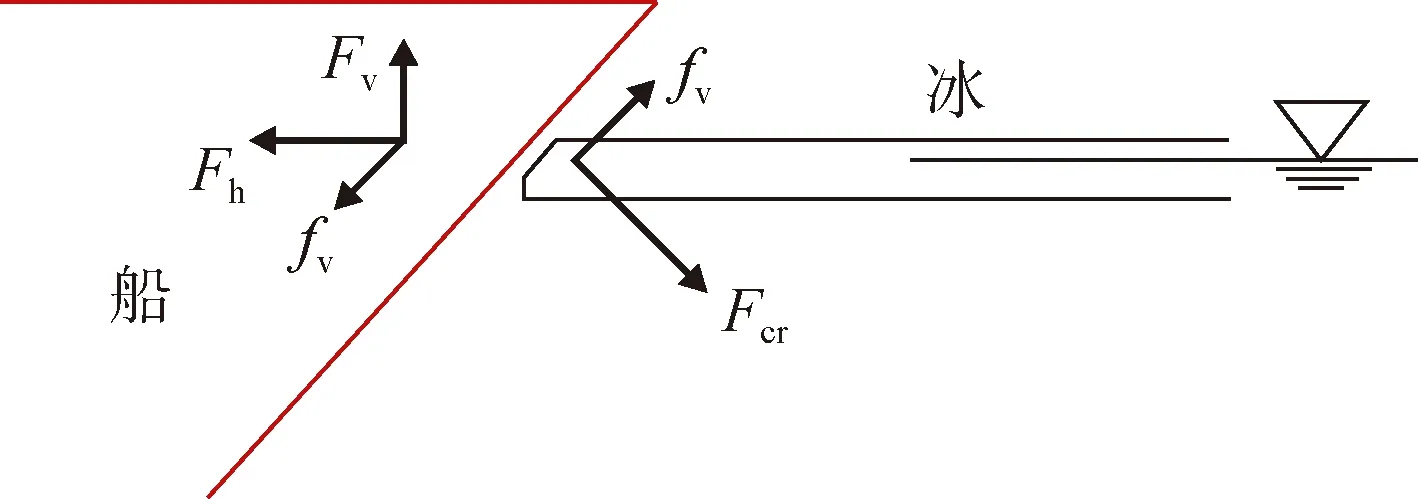
圖3 破冰結構與整冰的相互作用Fig.3.Interaction between ice and structure

破冰船的首尾等破冰結構在與冰體相互作用的破冰過程中, 考慮整冰與船體破冰結構的二維相互作用(圖3), 根據公式(4)可得:

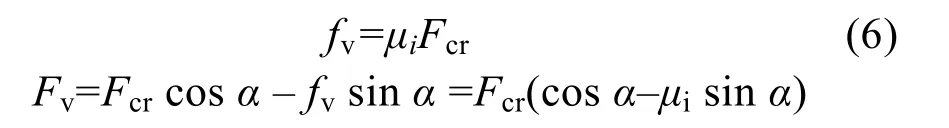
當船首尾結構的坡度角 α足夠大的時候, 作用在冰體上的力垂直分量Fv小至可以忽略。這意味著垂向冰力可能永遠不會超過冰的彎曲極限,因此陡峭結構破冰時不會發生冰的彎曲破壞。然而, 這并不現實, 在此前提下計算的冰力也不準確。依據公式(6), 坡度角的極限值依賴于冰與結構相互作用的摩擦系數。

破冰船破冰結構的坡度角對海冰冰體失效模式的影響是十分復雜的, 當 cosα–μisinα=0 時, 摩擦力系數與坡度極限角的關系可以如圖4所示,當破冰結構的坡度角大于極限角度時, 冰發生破碎失效; 當破冰結構的坡度角小于極限角度時,冰體發生彎曲失效。根據文獻[18], 北極海冰與船體結構的摩擦系數處于 0.05≤μi≤0.15, 由此依據圖4的關系, 可得極限角的范圍為 82°≤α≤87°。保守起見, 當坡度角大于 82°時, 使用彎曲失效模式將不再合理, 需要對失效模式進行進一步的探討。

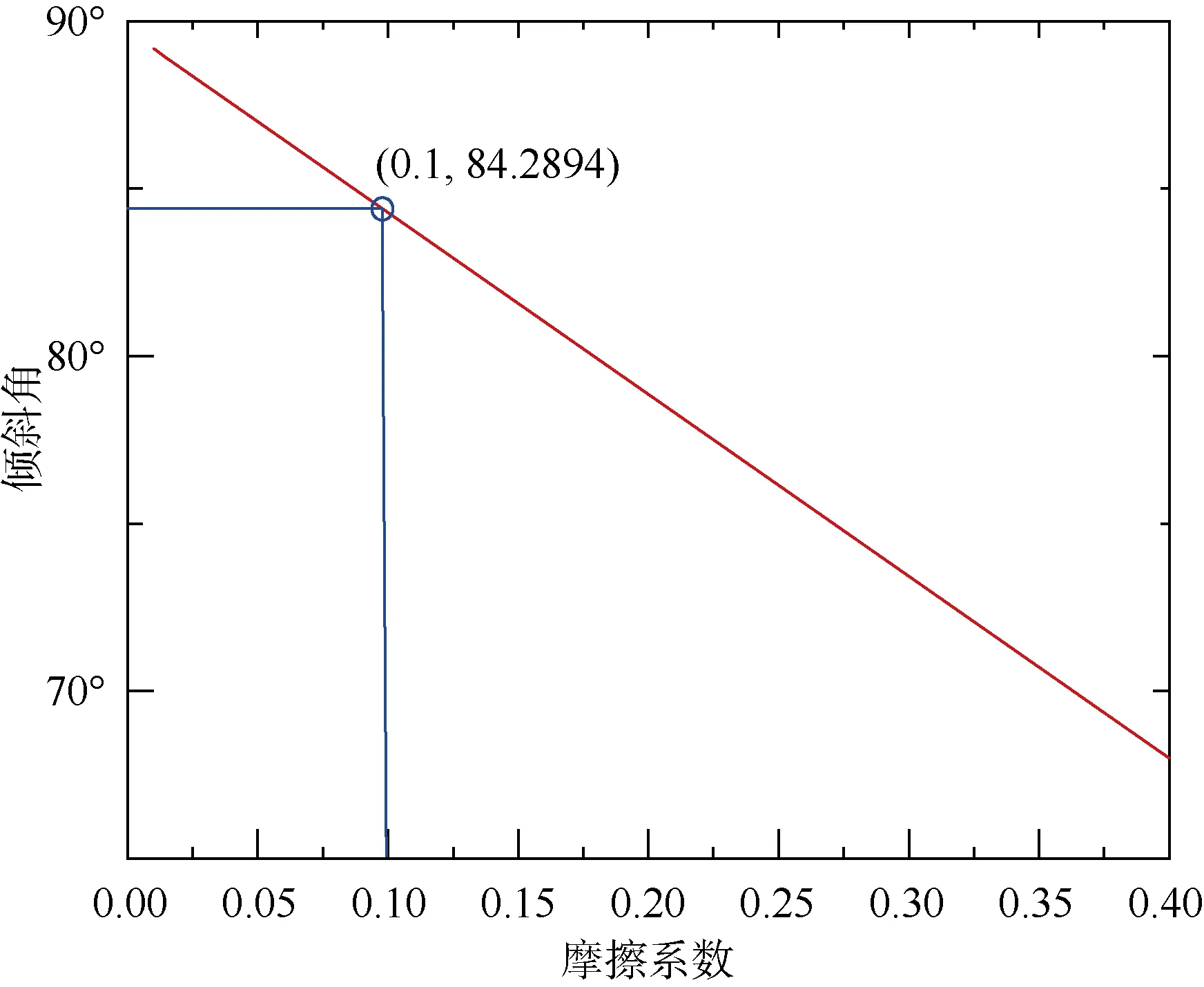
圖4 極限角與摩擦系數的關系曲線Fig.4.Relationship curve between limit angle and friction coefficient

關于破冰結構的傾斜角對冰失效模式的影響,文獻[19]通過試驗的手段進行了大量的研究, 給出了在不同坡度和冰速下冰體失效模式分布圖(圖5), 本文主要針對冰速較低的情況, 可以看出當傾斜角較小時, 冰的失效模式是彎曲破碎, 隨著坡度角的增大, 彎曲破碎的程度越來越小, 而當坡度角達到 70°時, 冰的失效模式主要是擠壓破碎。

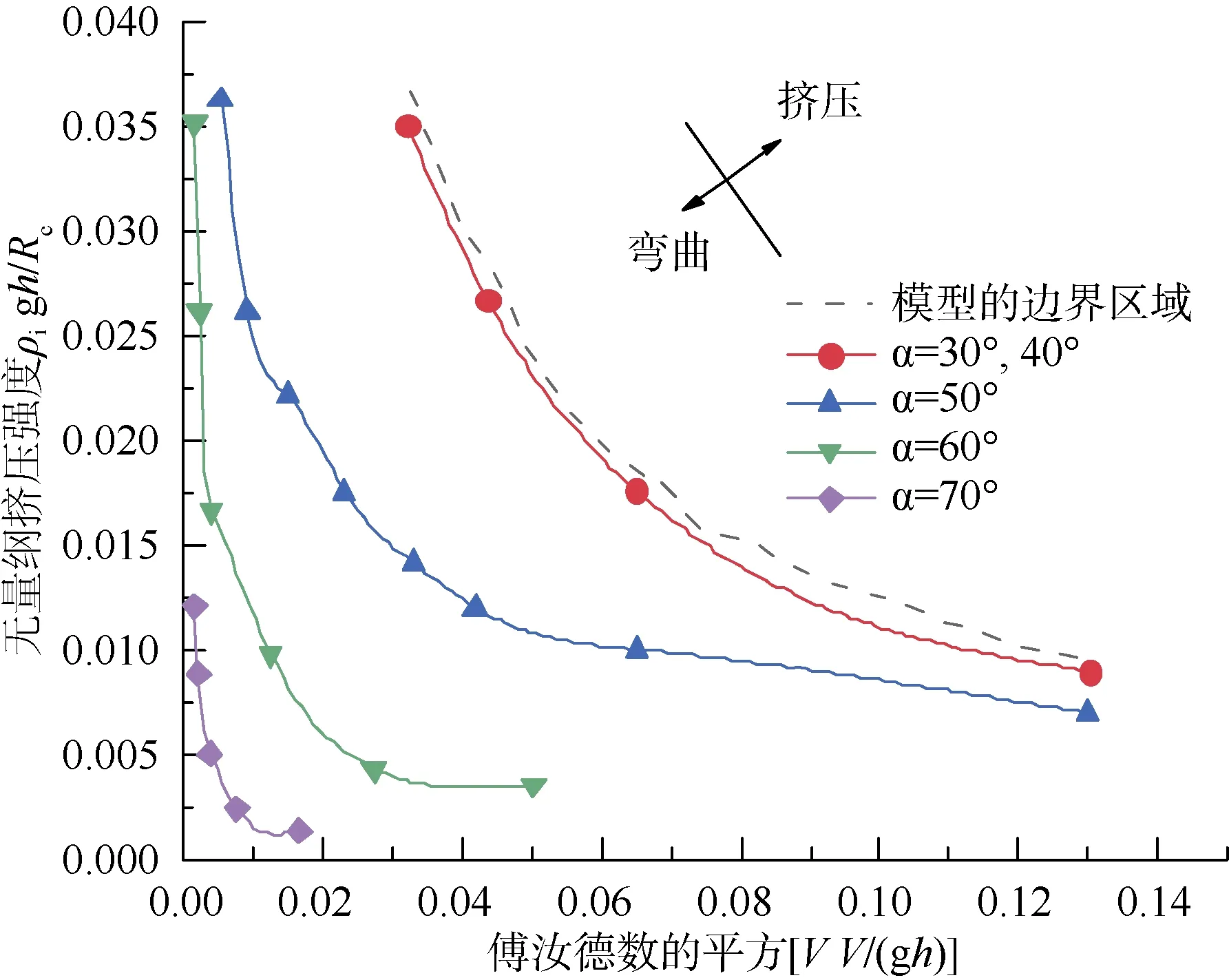
圖5 冰失效模式分布圖Fig.5.Distribution map of ice failure mode

因此, 可以說明, 在北極海冰的范圍內, 當破冰船破冰結構坡度角小于 70°的時候, 冰體發生彎曲破壞, 當坡度角處于 70°—82°時, 冰體同時發生彎曲和擠壓失效, 當坡度角大于 82°時,冰體僅發生擠壓失效。

當擠壓破碎模式發生時, 根據ISO 19906[20],在不考慮其他限制條件的情況下, 連續作用在結構體上的脆性局部擠壓力可以表示為

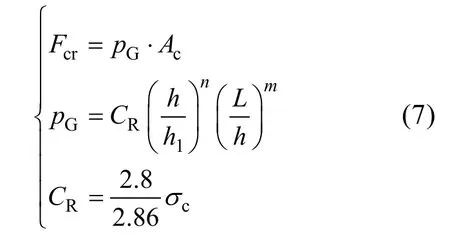
式中, pG為整體平均冰壓力; L為投影到結構物上面的跨度, 其單位是m; h為冰層厚度, 其單位是m;h1為1 m的參考冰厚; m=–0.16為經驗系數; n為經驗系數, 當冰厚小于1.0 m時, 等于 –0.50+h/5,當冰厚大于等于1.0 m時, 等于 –0.30; CR為冰的強度系數。

當結構物坡度角位于兩者之間時, 可以采用插值的方法, 來計算相應的冰載荷。

3 結論

通過破冰船破冰結構與整冰相互作用的力學分析, 得到了影響冰體失效的冰力分量與破冰結構參數的表達關系, 進而確認冰摩擦系數以及坡度角與冰體失效模式的關系, 依據北極海冰的摩擦系數范圍, 分析可得: 當破冰船破冰結構坡度角小于 70°的時候, 冰體發生彎曲破壞, 當坡度角處于 70°—82°時, 冰體同時發生彎曲和擠壓失效, 當坡度角大于 82°時, 冰體僅發生擠壓失效,同時給出了不同失效模式下冰力的計算方法。