問題驅動教學 探究生成智慧
——“分數的四則混合運算”教學設計

江蘇吳江經濟技術開發區天和小學（215000）

【教學內容】蘇教版教材的“分數的四則混合運算”

【教材分析】本節內容被放置于六年級上冊，是學生在掌握了基本分數的加減乘除運算之后進一步的學習內容。教材內容設置合理，難易適中，但是擴展性較弱。

【設計思路】采取了“問題驅動式教學”；在問題的引導之下開展新課引入、學習新知和概念深化的教學環節；通過問題引導學生思考，提升學生的綜合能力。

【教學目標】

1.理解并掌握分數四則混合運算的運算順序,并能按運算順序正確計算;體會整數運算律在分數運算中同樣適用,能運用運算律進行有關分數的簡便計算。

2.培養觀察、比較、分析和抽象概括能力。

3．在討論交流學習過程中,體會數學知識的內在聯系,積累數學學習的經驗。

一、設置懸念，引入新課——引導學生思考新舊知識的聯系

師：在之前的課程中，我們已經學習了分數的加減乘除四則運算了，那么僅僅依靠簡單的四則運算就可以列出式子了嗎？請思考問題：小彩燈是經常用來布置教室的道具。短的小彩燈每一段用4分米的電線，長的小彩燈每一段用6分米的電線，兩種小彩燈各做18段，一共需要用多少米的電線？請列出算式。（（1）18×4+18×6；（2）18×（4+6））

【評析：課始，教師要做的就是吸引學生的注意力。教師利用實際生活中的問題引發學生的思考，由淺入深，通過先研究“能否利用簡單的四則運算解決”，設置懸念，引發學生的思考，同時提示學生還有進一步探究的可能性】

二、學習新知，探究算理——讓學生掌握知識的內涵

師：我將上面的問題換一下，看看大家利用以前的知識如何解答。做18段短的小彩燈和18段長的小彩燈一共用電線多少分米？

師：請回想一下，這是以前已經學習過的整數的四則混合運算，你能總結整數四則運算的順序嗎？分數的混合四則運算與整數的混合四則運算是否規則相同呢？

【評析：數學知識不是孤立存在的，教師需要幫助學生聯系舊的知識，從舊的知識出發探究新的知識，從而構成完整的知識體系。整數四則運算是學生已經掌握的知識，教師通過調動學生的回憶，讓學生將整數的規則擴展至分數混合四則運算當中，從而產生問題，開展探究。】

師：請按照你猜測的運算規則計算前面列出的兩個式子，并且對運算規則進行總結。

生：分數四則混合運算和整數四則混合運算的順序相同。先計算乘除法，再計算加減法，有括號先計算括號里面的。

【評析：學生自己動手計算，驗證自己的猜想，總結規則，從而提高了動手能力和歸納能力。對于學生而言，動手操作的過程可以幫助他們對新的知識建立更為直觀的認識，加深對知識的認識。】

師：觀察上面兩個算式，哪個算式更簡單，為什么？兩個算式之間存在什么聯系？

生：算式（2）更簡單，因為括號里面相加的結果為10。兩個算式的結果相同，符合乘法分配律。

【評析：通過比較、思考和討論，學生在對比的過程中發現整數的運算律在分數中同樣適用，培養了數學思維。】

【評析：例1的目的有兩個：其一，幫助學生鞏固分數混合四則運算的法則，加深學生的印象；其二，引入方程，使得學生將新舊知識聯系起來，提高解方程的能力。】

三、概念深化，總結歸納——形成完整的知識網絡

【問題系列1】

（1）現有兩輛火車從甲乙兩地出發，相對行駛，已知甲乙兩地相距600千米，從甲地開出的火車每小時行駛60千米，從乙地開出的火車每小時行駛75千米，請問：兩列火車何時可以相遇？

（2）兩列火車仍從甲乙兩地相對行駛，從甲地開出的火車行駛至目的地需要10小時，從乙地開出的火車行駛至目的地需要8小時，那么兩車需要多久可以相遇？

師：對于問題（1），兩列火車在相遇時，各走了多少路程？路程之間的關系是什么呢？請按照這個思路，列出計算式，并且進行計算。

生1：兩列火車行駛的路程之和為600千米。600÷（小時）。

師：問題（2）與問題（1）的已知條件有什么不同？

生2：問題（2）已知時間，但是沒有告訴我們路程和速度。

師：是的。是否可以假設路程為定值1，此時兩輛列車的速度就可以用我們常見的分數表示出來了？請大家自己進行計算。

生：3（小時）。

【評析：此應用題是小學數學中常見的相遇問題，通過四則運算可求解。在教學過程中，教師沒有使用傳統教學模式中的直接講授法，而是通過問題引導學生主動思考和探究，對比問題（1）（2）之間已知條件的差別，學生就能夠利用問題（1）的解題經驗，解答問題（2）。通過解答應用題，學生的邏輯思維能力得到了培養，對運算規則有了更深入的理解。】

【問題系列2】計算下列物體的表面積：

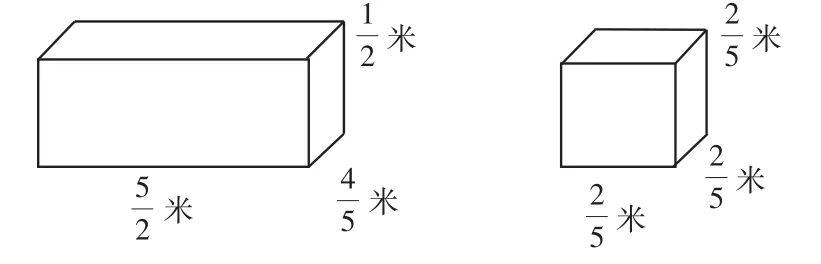
【評析：這一問題的設置是為了讓整個教學活動更有層次，讓學生理解代數與幾何之間的聯系。將立方體的邊長設置為分數，結合表面積公式巧妙地設計出了分數的混合四則運算，學生在解決問題的過程當中，自然就理解了分數運算的工具作用。】

師：分數四則混合運算的運算順序和整數四則混合運算的運算順序相同。但整數四則混合運算通常是一次計算出一個得數,而分數四則混合運算的乘除法連在一起時可以同時運算。在計算過程中需要注意“數字、符號有沒有抄錯;每一步的計算是否正確;書寫格式是否規范”。

問題驅動下的小學數學課堂，是探究性的課堂，也是層次分明的課堂。在問題的引導啟發下，學生一步步掌握分數四則混合運算的知識點，學會應用四則運算解決實際問題。在這個過程中，學生的自信心得到了提高，探究能力也得到了培養，學生從單純的知識接收者變成主動的學習者，數學課堂的效率也有所提升。