對一節計算教學課的思考

江蘇如東縣馬塘鎮王元小學（226401）

近日觀摩了一堂校內公開課，內容是蘇教版教材三年級“兩位數乘兩位數”。教師首先展示情境圖，啟發學生通過讀圖提取信息，然后詢問圖中透露的信息。學生回答：“訂一份學生奶，每月28元，一年需要多少元？”接著，教師要求學生列式計算。匯報展示時，教師隨機抽取三名學生上臺板演，他們不約而同地用豎式演算。

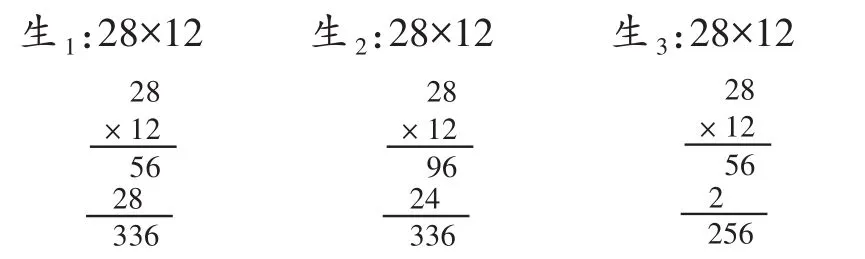
全班反饋交流時，教師評價生2的做法：“雖然結果也是336，但計算方法有誤，值得商榷。”其他學生紛紛發表自己的看法，但贊同的少，反對的多。這時，教師小結：“雖然生2的計算結果正確，但計算方法有誤，同學們應向生1看齊，計算兩位數乘兩位數時，應將第二個乘數拆分，這樣就可以用我們學過的兩位數乘一位數求解，即拆分乘數12，先用2乘28，再用10乘28……”接著，教師用所謂“正規方法”的標尺來評價生3的豎式，并著重指出錯處和造成錯誤的原因。最后，教師又重新演示了一道標準豎式作為模板，并用紅色粉筆標注每一步的計算過程。

一、改變算序，異曲同工

在課后訪談時，我們和授課教師、生2進行面對面交流，生2陳述了自己的演算過程：“我分兩步計算，先用8乘12，得到96，再用20乘12，得到240，最后累計96+240=336（元），就是一年需要的錢。”

我們仔細斟酌和推敲，生2的思路雖然很特別，但其實也符合算理，與所謂的“正規方法”有異曲同工之妙。

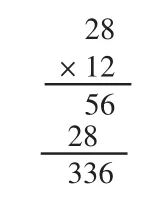
圖1

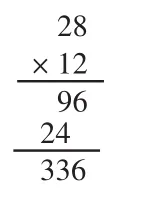
圖2

圖3

對于生1的“正規方法”（如圖1），算理分解如下：把12個月分為2個月和10個月，第一步計算2×28=56，即2個月所需的錢；第二步計算10×28=280，即10個月所需的錢，最后由56+280=336（元），就能知道一年所需的錢。

對于生2的做法（如圖2），算理分解如下：把28元分為8元和20元，第一步計算8×12=96，表示每月月頭征收8元訂金，12個月就是96元；第二步計算20×12=240，表示每月月末征收20元尾款，12個月就是240元，因此12個月的訂金和尾款合起來就是96+240=336（元）。

以上兩種算法，其實就是乘法分配律的豎排版，生2的做法應該交換兩個乘數位置（如圖3），這樣看來更合理。換言之，生2的算法在算術和算理上都是過關的，只是生2使用的格式不同于常規，容易引起他人誤會。

二、誰乘誰，并無分別

案例中，授課教師之所以極力否定生2的算法，并不是教師本人不理解，歸根結底，其實是教師在極力維護自己的權威，維護傳統的權威。多年來積累的豎式“經驗”讓教師墨守成規，也可以說，按照這種經驗從未出錯，所以對其深信不疑。

當然，我們不能把原有經驗一棍子打死，但我們可以在充分尊重原有經驗的基礎上，去鑒別和接納“經驗”以外的新鮮事物，吐故納新，不斷保持生命力。教學時，如果教師能慢下來，耐心傾聽學生的心聲，那么教師和其他學生都會受到啟發，有所發展。

其實，新型算法正體現了生2對乘法豎式結構深入細致的認知。在用豎式計算多位數乘以一位數時，自上而下和自下而上本身沒什么區別，如計算“124×3”時，第一步計算4乘3或3乘4其實沒什么不同，都是同一句口訣，只是感覺上有先后差別而已。這是生2當時的心理狀態，但沒引起授課教師的注意。

三、經驗之后，孕育創新

在教學“用豎式計算124×3”后，教師通常都是照本宣科，提出用交換律來驗算，但驗算的目的僅僅在于結果的一致性，對于“豎式驗算時，交換兩個乘數的位置，乘積為什么不變”沒有進行深入的思考。如果教師能打破常規，在學生發出“不和諧”的聲音時，以包容的姿態，大大方方讓新方法和舊方法來一次正面交鋒，就會促進學生的認知更有深度。

要想進步，經驗必不可少，經驗也是教師走向成熟的重要條件，但任何經驗都是一把雙刃劍，它是發展變化的，如果因循守舊、無視甚至排斥這種改變，那么就會搬起石頭砸自己的腳。