深化“平均分”教學，為“除法”奠基

廣西玉林市博白縣黃凌鎮中心小學（537636）

日常生活中，小學生分配物品的經驗豐富，但沒有形成有效策略。教學中通過讓學生動手分物品，切實感受平均分配的動態過程，明確“平均分”的運算意義，建立均分模型，再引入除法概念就顯得順理成章了。在具體教學過程中，有以下方面值得注意。

一、分配對象多樣化，重視語言表述

教材都是安排對一定數量物品進行分配，形式單一。教學中，可以創新分配對象，如圖1、圖2、圖3，分別對線段、面積和角進行平均分，使分配關系不再限于數量多少，而擴大到幾何學上的相等，甚至拓展至重量、濃度、厚度……大大豐富均分對象和量標。

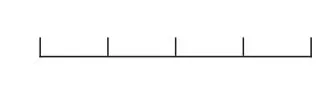
圖1

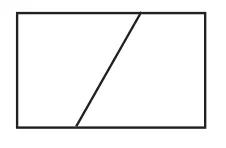
圖2

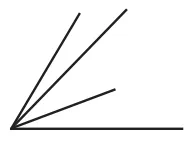
圖3

用除法表示平均分，被除數就是總數，除數是每份數（份數），商是份數（每份數）。因此，操作活動前，教師要設法引起學生的注意：分什么物品？分配原則？分配結果？緊扣這三個問題，邊想邊做，學生的動手能力、理解力和表達能力都會同步增長，完成由“平均分”向“除法”的進化，充分發揮平均分對于除法的價值。筆者覺得，這個過程可以分四個層次進行教學。

第一層次：能看懂教材，或聽懂教師講授的內容，并按要求實施均分。如填空題：15個杧果，每5個放一盤，一共可以放（ ）盤。審題：均分對象是杧果，論個算；分配方法為5個放一盤；分配結果是一共可以放3盤。

第二層次：根據平均分的結果，讓學生口頭簡述分配情況，再次感知分配過程。

第三層次：補敘他人分配的過程與結果。

第四層次：根據分配結果還原分配始末。

二、分算結合，引導學生想象均分

除法可以視為連續相減的簡便運算，乘法和除法互為逆運算，除法與減法、乘法都有關聯。教材安排“連減求商”和“想乘算除”，有效溝通了除法和減法、乘法之間的關系。但長此以往，學生就會只推崇“想乘算除”，對“連減求商”則感到麻木和抵觸。更為不利的是，本課的重點是“口訣求商”，于是除法與減法的關系就被淹沒了。因此，在學習除法的準備課“平均分”時，有必要創設“分中有算，邊分配邊計算”的活動。

如，出示一盒餅干，共計18塊，每3塊放一堆，放了5堆后，問：“還有沒有擺出的餅干嗎？”讓學生嘗試用不同方法列式：

加法：3+3+3+3+3=15；

乘法：3×5=15；

減法：18-3-3-3-3-3=3。

通過這樣的活動，使學生感受到平均分與加法、減法和乘法的聯系，重點體驗平均分與減法的關系。若學生對均分對象沒有抽象出輪廓，進行抽象形態分配，就直接跳到抽象概念，遺患無窮。分是為了不分，當學生汲取了一定的分配經驗后，可以脫離實物，進行想象分配。可以在實物分到一半時，撤去實物，延續先前的思路繼續分，也可以從一開始就脫離實物，全程想象分配。

通過想象分配，可以促使學生逐步擺脫實物的依賴，形成抽象思維。

三、變被動為主動

有一道題：2張紙可以做8朵花，那么5張紙可以做（ ）朵花。有部分學生先算2×8，后面就卡殼了。究其原因，是因為2和8關系特殊，它們既可以組成除法算式“8÷2=4”，又能組成乘法算式“8×2=16”，使學生感到困惑。如果將題干改編為“3張紙可以做12朵花”，則可避免出錯，因為學生還沒有學到3×12。學生之所以連蒙帶猜，說明學生無法準確捕捉均分信號，以前課本中的均分信號十分明確，讓人一目了然，而這道題中的卻十分隱晦，既沒有說明要平均分，均分的主體也不明確，導致部分學生無從下手。

還有一道類似題：有8噸天然氣，用了5天，求平均每天消耗幾噸？每噸可以維持幾天？學生知道用除法卻總分不清用誰除以誰，主要原因在于分不清分配主體和接受分配的載體，即把誰分給誰。歸根結底，還是因為缺乏分配經驗。為此，教師不妨安排如下辨別練習：4塊巧克力8元錢，想一想，1塊巧克力幾元錢？1元錢可以買幾塊巧克力？“1塊巧克力幾元錢”可以這樣想：將8元錢平均分配給4塊巧克力，就可以得到每塊巧克力對應的錢數。“1元錢可以買幾塊巧克力”可以這樣想：將4塊巧克力平均分配給8元錢，此時錢數是接受分配的載體，巧克力是分配主體，就可以得到1元錢對應的巧克力數。

平均分不僅是一個機械的分配過程，也不僅是一個揭示除法意義的實踐操作活動，它還蘊含著加、減、乘、除四則運算的邏輯關聯，因此，巧妙地運用各種算法來審視分配過程，有助于學生對除法的全面理解。