履帶-地面耦合系統機理分析與建模

姚 禹， 王 博， 高 智

(1.長春工業大學 應用技術學院， 吉林 長春 130012;2.長春工業大學 汽車工程研究院， 吉林 長春 130012;3.長春市軌道交通集團有限公司， 吉林 長春 130012)

0 引 言

工程機械地面力學是地面力學的一個重要組成部分，目的是研究工程車輛的行走系統和與其接觸的地面土壤之間相互作用關系[1-2]。由于履帶車輛的行駛能力較強，履帶車輛地面力學已引起國內外許多學者的廣泛關注。早期，Bekker等[3-4]開創了地面力學經典理論，利用純經驗和半經驗的研究方法對履帶車輛行駛時壓力導致地面土壤的下陷量進行研究，取得了一系列的研究成果，并且至今仍在使用。但是，履帶與地面是相互作用的，車輛通過履帶將重力、驅動力作用到地面土壤上，地面土壤又將地面摩擦、推土等行駛阻力通過履帶反作用給履帶車輛。以往研究中，以履帶或地面土壤做單一研究對象的研究成果較多[5-7]，且履帶與地面土壤的相互作用受力關系十分復雜。隨著履帶車輛的不斷發展，對履帶-地面間的相互作用關系進行定量描述，建立履帶-地面耦合系統數學模型，利用地面力學特性參數和履帶行走機構特性參數分析履帶車輛的通過能力和牽引特性已經變得越來越重要。

針對上述問題，在現有地面力學的研究基礎上，文中提出履帶-地面耦合系統的概念，建立履帶-地面耦合系統數學模型，利用地面力學特性參數和履帶行走機構特性參數對履帶-地面耦合系統進行機理分析，建立履帶-地面耦合系統的摩擦力和側面推土力受力數學關系，揭示履帶-地面耦合系統的機理規律，為履帶車輛通過性和牽引特性研究提供基礎。

1 地面力學基本理論

根據地面力學理論，履帶車輛在地面土壤上行駛時，履帶行走機構會對地面土壤產生力的相互作用，即土壤的法向力和切向力。其中，垂直于地面土壤的力為履帶-地面耦合系統的法向力，它可以表征地面的承載能力；水平于地面土壤的力為履帶-地面耦合系統的切向力，它可以表征地面的抗剪切能力。經過大量實驗和力學理論計算，給出了履帶-地面耦合系統的法向力和切向力的半定量數學關系。

1)根據經驗關系式，土壤的法向應力σ與地面變形的關系為[8]：

(1)

式中:kc----履帶-地面耦合系統的粘聚力模量;

b----履帶寬度;

kφ----履帶-地面耦合系統的摩擦力模量;

z----履帶-地面耦合系統的垂直變形量;

n----履帶-地面耦合系統地面下陷指數。

2) 履帶-地面耦合系統的切向力為[9]：

Fx=Ac+Wtanφ(2)

式中:A----履帶的支撐面與土壤的接觸面積;

c----履帶-地面耦合系統的粘聚系數;

W----履帶車輛的垂直載荷；

φ----履帶-地面耦合系統的摩擦角。

根據庫侖公式，由式(2)得到履帶-地面耦合系統的最大剪切應力為：

τmax=c+σtanφ(3)

由式(1)～式(3)可知，履帶-地面耦合系統的受力情況不僅與履帶車輛的載荷、履帶接地面積等履帶車輛行走機構的特性參數有關，同時與土壤粘聚系數、土壤摩擦角等土壤力學特性參數也密切相關。而土壤力學特性又是十分復雜的，不僅不同類型的土壤，其土壤力學特性不同，即便相同類型的土壤，隨著含水量的變化，土壤力學特性也截然不同。故此，為更好地分析履帶-地面耦合系統的相互作用關系，需要對履帶-地面耦合系統進行數學建模。

2 履帶-地面耦合系統模型

履帶-地面耦合系統的受力關系發生于履帶車輛在地面土壤上行駛的任何時刻，對履帶-地面耦合系統機理進行分析，發現履帶板的支撐面、履刺表面和側面與土壤有力的相互作用。此外，履帶相對土壤運動時對堆積在履帶旁邊的土壤也有力的相互作用。將履帶板的支撐面、履刺表面和側面與土壤的相互作用稱為履帶-地面耦合系統的摩擦力，履帶相對土壤運動時對堆積在履帶旁邊土壤的相互作用稱為履帶-地面耦合系統的側面推土力。

2.1 履帶-地面耦合系統的摩擦力

由于履帶-地面耦合系統受力情況復雜，直接對履帶-地面耦合系統的摩擦力求解是非常困難的，也是不準確的。故此，引入微分思想，將履帶劃分成若干個微元dxdy，如圖1所示。

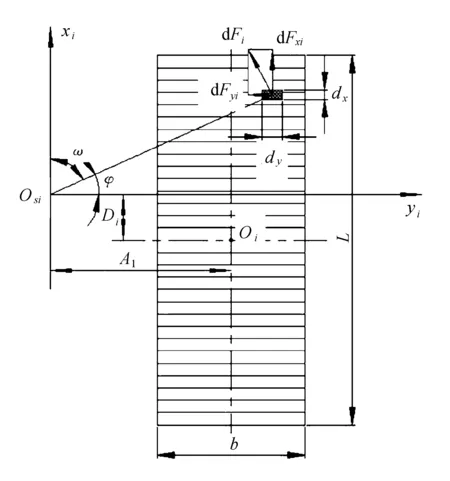
圖1 履帶-地面耦合系統的摩擦力受力分析

首先對作用在每一微元dxdy上的摩擦力dFi求解：

dFi=μpdxdy(4)

式中:μ----履帶-地面耦合系統的摩擦系數;

p----履帶車輛的接地比壓;

i----第i條履帶(i=1,2)。

而后，將微小的摩擦力dFi投影到xi軸和yi軸得：

(5)

對式(5)兩邊進行積分，得到履帶-地面耦合系統的摩擦力在xi軸和yi軸上的投影為：

(6)

式中:l----履帶長度;

Ai----履帶車輛的橫向偏移量;

Di----履帶車輛的縱向偏移量;

Fzi----第i條履帶的載荷。

最后，式(6)由力矩平衡原理可得履帶-地面耦合系統的摩擦阻力矩為：

?(y-Ai)dFxi-?(x+Di)dFyi=

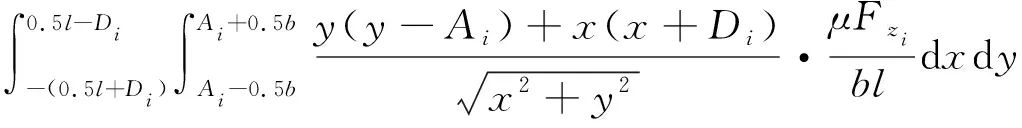
2.2 履帶-地面耦合系統的側面推土力

當履帶車輛在松軟地面上行駛時，履帶-地面耦合系統除了受到摩擦力外，還受到履帶相對土壤運動時對堆積在履帶旁邊的土壤產生的側面推土力。由Bekker的壓力-下陷關系，履帶在松軟地面的下陷量為[10]：

(8)

履帶相對土壤運動時對堆積在履帶旁邊的土壤產生側面推土力時的受力情況如圖2所示。

履帶-地面耦合系統主要受到履帶下部土壤對楔形土的作用力N，土壤單位面積上的內聚力C和單位長度的推土力R。圖中，F為單位長度的土楔重量，由于履帶側面刮起土壤的質量極小，導致F對履帶-地面耦合系統的影響微乎其微，所以為方便說明問題，在下面的討論中忽略不計[11-12]。

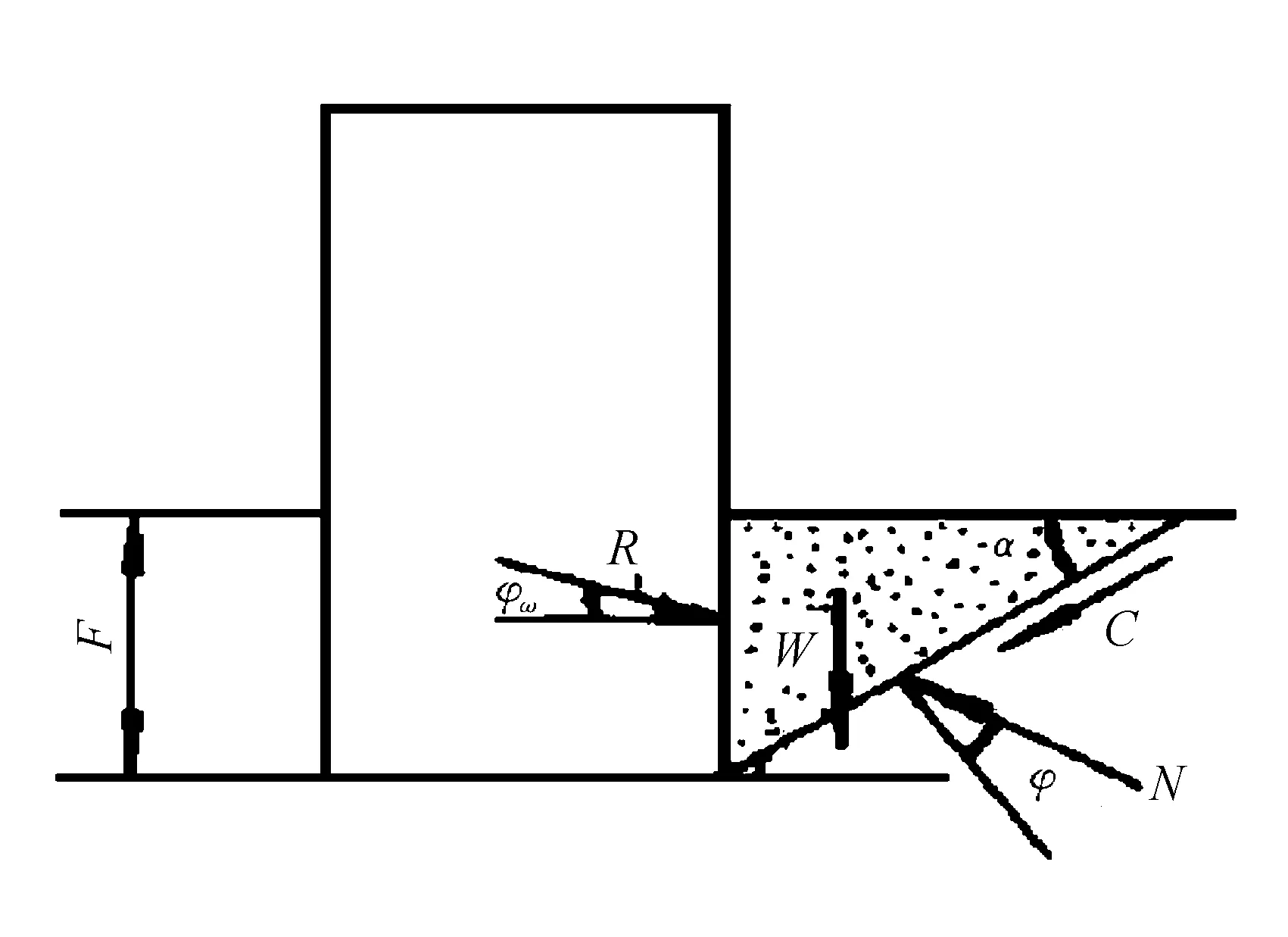
圖2 履帶-地面耦合系統的側面推土力受力分析

由圖2可知，履帶-地面耦合系統在Y軸和Z軸方向上受力平衡。根據力的平衡原理，有：

∑Y=Rcosφω-zCcotα-Nsin(α-φ)=0 (9)

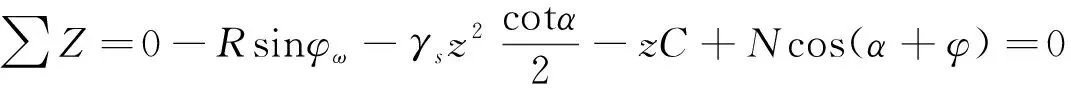
式中:α----破壞面角度;

φω----板壁摩擦角;

φ----土壤內摩擦角;

γs----土壤容重。

由式(9)和式(10)可得單位長度的推土力為：

(11)

由式(11)很難求出側面推土阻力R的準確數值解。但是觀察式(11)不難看出,單位側面推土阻力R是破壞面角α的函數，R的最小值對應著一定的α值。故此，采用求導的方法來求解Rmin。為了方便計算，將式(11)整理成如下形式：

(12)

式中:

k3=cosφωcotφ-sinφω

u1=zCcotφ

u2=-cosφω-sinφωcotφ

對式(12)進行求導計算，得：

(13)

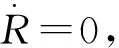
(14)

考慮到破壞面角α的實際意義，取：

(15)

(2Di+l)Rmin·cosφω(16)

履帶-地面耦合系統側面推土產生的阻力矩為：

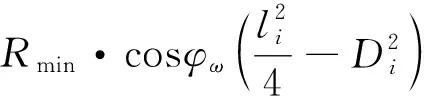
根據式(1)～式(17)對履帶-地面耦合系統的機理分析，履帶車輛在松軟土壤上行駛時，履帶-地面耦合系統的模型為：

(18)

3 數值計算及仿真分析

某型履帶車輛的主要技術參數見表1。

表1 某型履帶車輛的主要技術參數

計算及仿真時所需的各松軟土壤的主要特征參數見表2。

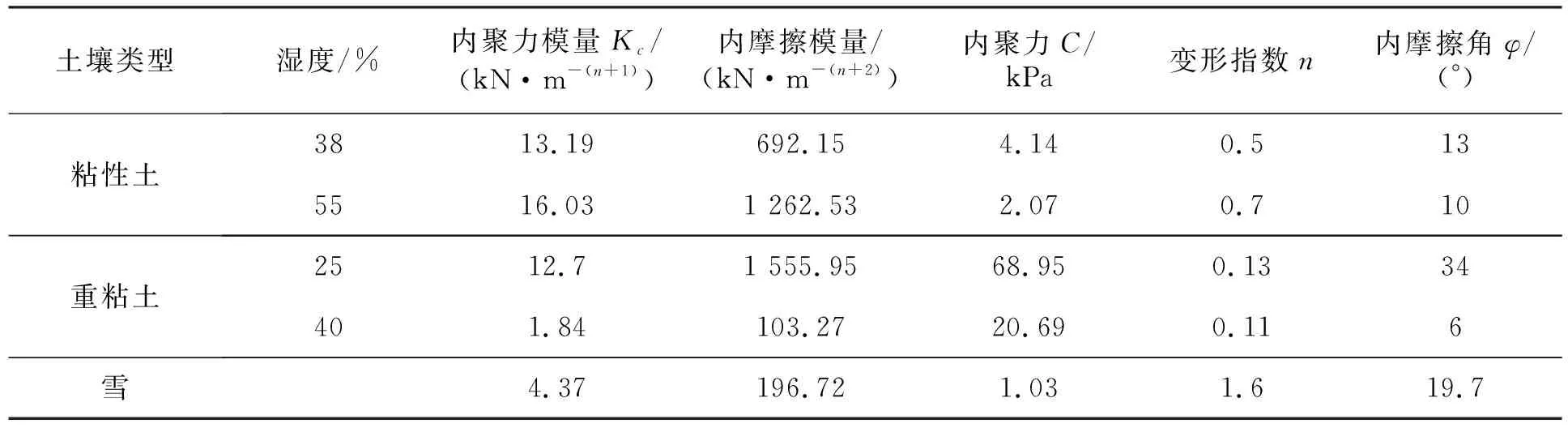
表2 各類型土壤力學特征參數

將表1和表2的參數代入式(1)～式(18)中，即可得履帶車輛行駛時的履帶-地面耦合系統數學模型。為了驗證履帶-地面耦合系統模型的準確性，并進一步分析履帶-地面耦合系統在各松軟土壤條件下的受力情況，利用Recurdyn進行仿真研究。履帶-地面耦合系統的三維模型如圖3所示。

圖3 履帶-地面耦合系統三維模型

文中主要研究履帶-地面耦合系統的數學模型問題，即履帶與地面相互作用的受力情況。而履帶車輛是通過履帶板將載荷作用到地面土壤的，地面土壤也是通過履帶板將摩擦力等反作用給履帶車輛的。故此，用履帶板的受力情況即可來表征履帶-地面耦合系統的受力情況。

分析履帶-地面耦合系統在濕度38%的粘土和濕度40%的重粘土及雪三種土壤條件下履帶板的受力對比情況，將履帶板的受力進行分解，水平于履帶板的受力為履帶-地面耦合系統的縱向力，來自于履帶車輛的行駛阻力，它可以表征土壤的抗剪切特性，如圖4所示。

垂直于履帶板的受力為履帶-地面耦合系統的垂向力，來自于履帶車輛及上方負重輪的載荷，它可以表征土壤的承壓特性，如圖5所示。

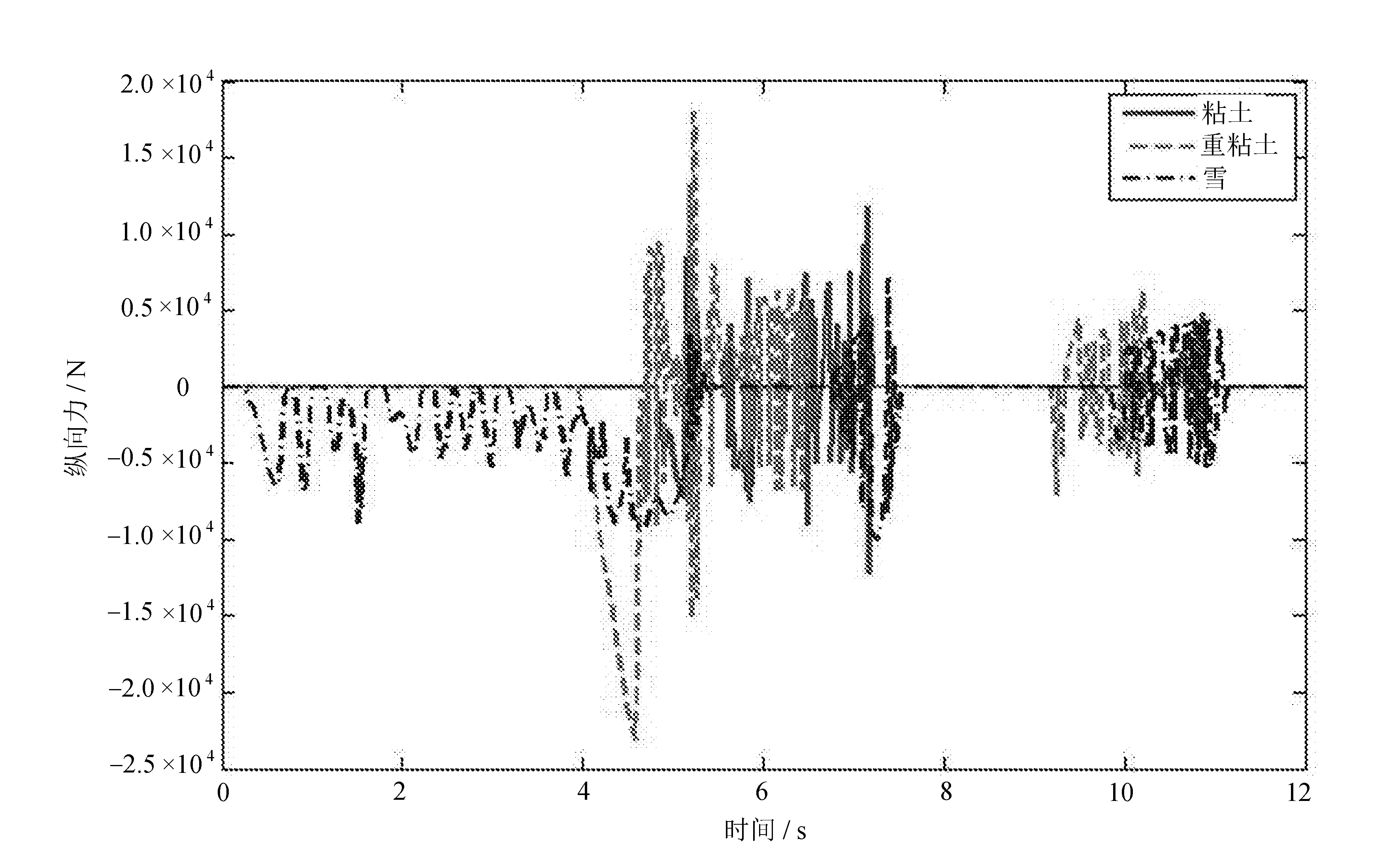
圖4 履帶-地面耦合系統在三種土壤類型下縱向受力情況

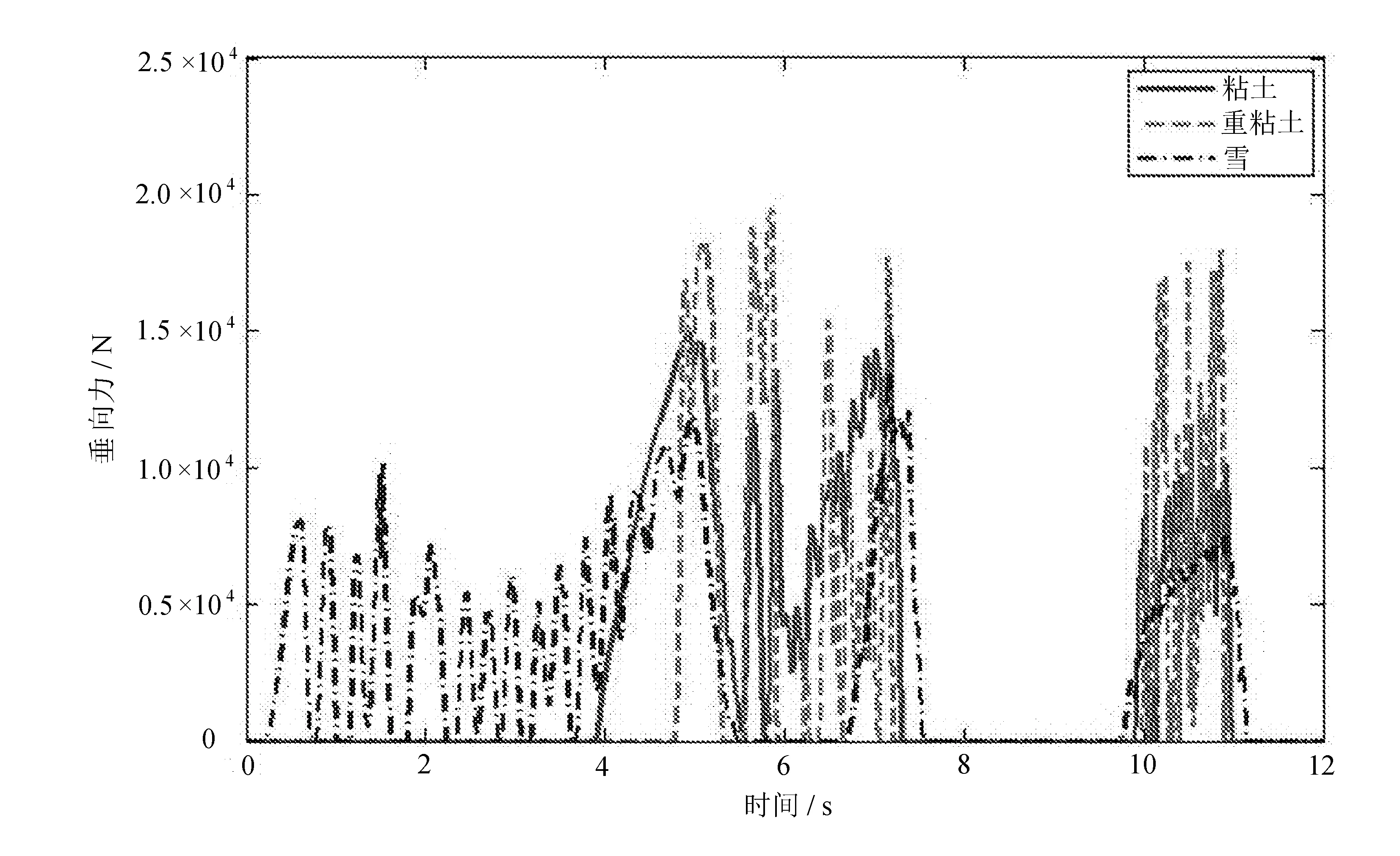
圖5 履帶-地面耦合系統在三種土壤類型下垂向受力情況

由于履帶車輛在行駛過程中履帶時刻繞卷地面，故圖4和圖5履帶-地面耦合系統的受力情況也是呈周期性變化。其平均值與履帶-地面耦合系統數學模型理論計算值基本相近，驗證了文中履帶-地面耦合系統模型的有效性。

4 結 語

對履帶-地面耦合系統進行機理分析與建模。針對以往研究中以履帶或地面土壤做單一對象而忽略了履帶與地面相互作用的問題，提出履帶-地面耦合系統的概念。通過地面力學基本理論，建立了履帶-地面耦合系統數學模型。通過對履帶-地面耦合系統相互作用時摩擦和側面推土產生的力進行機理分析，分別建立了履帶-地面耦合系統中摩擦力和側面推土力的數學關系。利用地面力學特性參數和履帶行走機構特性參數對履帶-地面耦合系統進行了定量描述。

利用Recurdyn軟件建立三維模型對履帶-地面耦合系統的理論研究進行仿真驗證。仿真分析驗證了所提模型的準確性，也進一步揭示了履帶-地面耦合系統的機理規律。該模型可為履帶車輛的通過性和牽引性研究提供基礎。