基于二次B樣條的有限元法

秦丹丹， 商玉鳳， 黃文竹

(1.空軍航空大學 基礎部， 吉林 長春 130022；2.貴州醫科大學 生物與工程學院， 貴州 貴陽 550004)

0 引 言

微分方程作為一類重要的數學模型，被廣泛應用于物理、化學、生命科學和環境科學等領域。目前，廣大科學工作者已經對微分方程做了深入研究，并將微分方程做了系統的分類。若按照未知數的個數進行分類，可以分為常微分方程(Ordinary Differential Equation， ODE)和偏微分方程(Partial Differential Equation， PDE)，其中偏微分方程又可以細分為橢圓型、拋物型和雙曲型方程。若按照方程中最高階導數的階數進行分類，可以分為一階微分方程和高階微分方程。若微分方程中算子為線性算子，此微分方程為線性微分方程，否則即為非線性微分方程，這里線性微分方程又可以細分為齊次線性和非齊次線性微分方程。大多數微分方程無法求出精確解，這就要求人們用各種數值計算方法求取方程的近似解，并分析數值方法的誤差與收斂階。常用的方法包括差分法、有限元法和有限體積元法等。可以說，微分方程的數值解法仍然是值得研究的一類問題。

樣條函數自出現以來就在插值逼近和偏微分方程數值解方面有廣泛應用。B樣條是樣條函數的一個重要分支。由于B樣條函數是對稱單峰值函數，并且具有光滑性好、緊支集等特點。二次B樣條的光滑性要優于Lagrange型二次元。這兩種基函數對應的剛度矩陣規模相差懸殊，前者系數矩陣的階數遠遠低于后者，而二者的收斂精度卻相同。以B樣條為基函數的有限元法生成的系數矩陣仍然能夠保證稀疏性、對稱性和正定性，便于上機實現。基于以上考慮，構造了以二次B樣條為基函數的有限元法。

1 B樣條簡介

文中用到的是等距B樣條函數。

定義1m階B樣條的卷積定義式[1-3]：

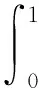
m≥2

其中

B樣條具有很多優良性質：

1)正定性與緊支集，Sm(x)≥0，支集為[0,m]；

2)分段光滑性，Sm(x)是一個分段m-1次多項式，Sm(x)∈Cm-2(-,)；

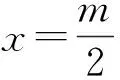
4)成立積分遞推式

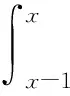
及代數遞推式

其中,m=1,2,…。B樣條其他性質參見文獻[2]。

按照遞歸定義、積分遞推式和代數遞推式均可以計算出B樣條的表達式，二次B樣條的解析表達式如下：

2 有限元格式

考慮兩點邊值問題：

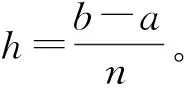
i=-2,-1,…,n-1

接下來，我們將前兩個函數換成[4-5]：

將最后兩個函數換成線性組合：

由于變換為線性運算，變換前后的兩個空間是等價的。記Uh為以二次B樣條為基函數的函數空間。為方便起見，我們仍將基函數記為{φi(x)}。接下來，我們考慮的是零邊值問題，即α=β=0。

文中考慮的模型是零邊值問題，所以有限元空間Uh的基函數為:

令

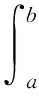
則兩點邊值問題的有限元格式為[6-9]：

使得

a(uh,vh)=(f,vh), ?vh∈Uh

a(u,v)是對稱正定的雙線性形式，變分形式有唯一解。應用分部積分公式可以得到

其中

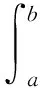
求解出ci即可得到近似解uh(x)，從而算出任意點處的函數值及一階導數值。系數ci不像Lagrange型二次元那樣直接就是整數節點和半整數節點處的函數值，但經過簡單的計算就能夠求出相應的值。由于B樣條具有緊支集

中最多只含有三個非零項。特別地，節點xi處的函數值為

uh(xi)=ci-2φi-2(xi)+ci-1φi-1(xi)

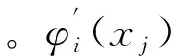
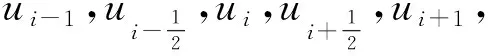
3 數值算例

取a=0，b=1，p=0，f(x)=4π2sin(2πx)，兩點邊值問題的精確解為u(x)=sin(2πx)。應用MATLAB編程得到數據見表1。

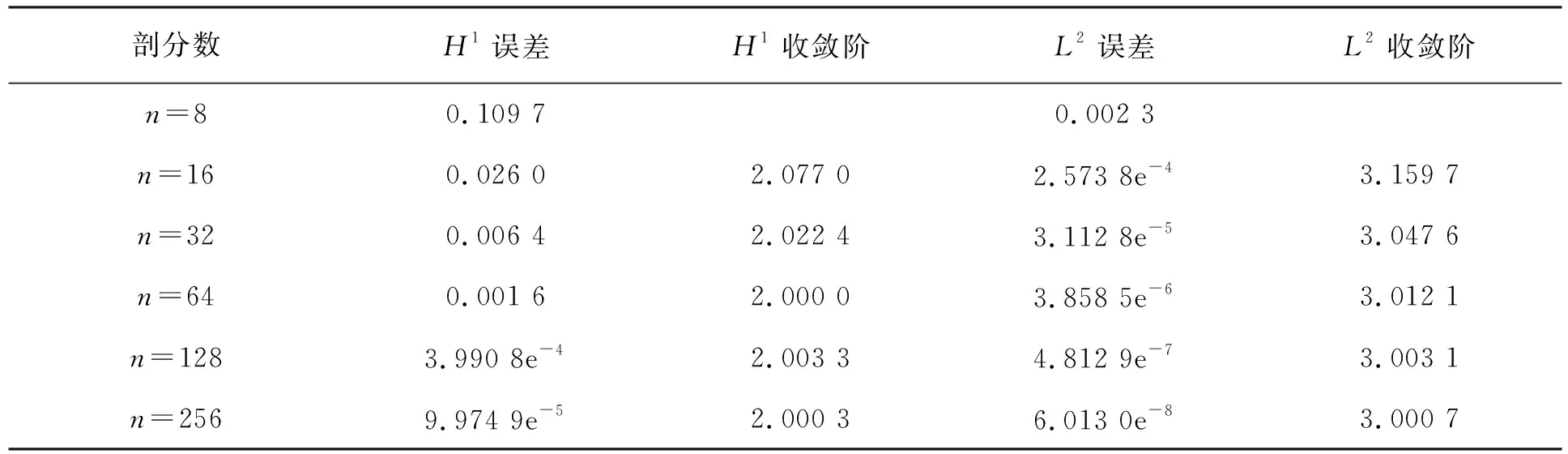
表1 有限元格式的誤差與收斂階

表1給出了H1半范數和L2范數下的誤差，比較發現誤差不僅是遞減的，而且分別以2階和3階的速度收斂。這說明我們構造的二次B樣條有限元格式是有效的。

4 結 語

構造了基于二次B樣條的有限元格式，該方法能夠達到最優收斂階。在H1半模和L2模下，收斂精度分別是2階和3階。我們發現B樣條有限元法與傳統有限元法一樣有較高的收斂階，還具有一些優于傳統有限元法的性質。

對于兩點邊值問題，作者分析過一至三次B樣條的有限元法和有限體積法[3]。B樣條還可以推廣到多元情形，希望未來能利用B樣條處理一些偏微分方程的數值計算問題。