基于輪間耦合力最小的四輪獨立驅動電動汽車驅動力分配方法

易 星 張 云 馬雷

（1.江西科技學院，江西 南昌 330098；2.燕山大學，河北 秦皇島 066004）

1 引言

環境污染與能源緊張已成為當今焦點問題，開發無污染，低能耗汽車成為迫切之需。電動汽車是汽車研究領域的熱點之一。四輪獨立驅動電動汽車可實現底盤電子化和主動化，使其與傳統汽車相比具有更強的競爭力[1]。對于四輪獨立驅動電動汽車驅動力分配方法，國內外學者進行了相關研究：文獻[2、3]通過仿真分析，主要根據各驅動輪的縱向和側向附著建立二次型評價函數，利用優化理論使車輛各驅動輪縱向和側向附著最小，來實現驅動力分配，但優化時，需精確估計各車輪的側向力；文獻[4、5]利用輪胎模型，將輪胎側向力近似用縱向力表示，建立驅動力分配目標函數，并進行了仿真實驗，但在計算輪胎側向力時需得到車輪側偏角和滑轉率。綜上所述，雖然相關驅動力分配方法在仿真條件下能取得較好效果，但有些物理量無法用傳感器測量不利于工程實際應用。

以四輪獨立驅動電動汽車為研究對象。首先，分析某一驅動輪的受力情況及輪間耦合關系，得到輪間耦合力F的解析式，并分析F對車輛行駛動力性和穩定性的影響。然后，將F轉化為對應驅動轉矩作為目標函數；綜合考慮影響驅動力分配的條件來確定約束條件，并確定約束條件中橫擺轉矩MZ的求解；最后，設計整車控制方法并建立ADAMS與Matlab聯合仿真模型，通過分析仿真和實車實驗結果，證實了基于輪間耦合力最小的驅動力分配方法的有效性和合理性。

2 驅動力分配策略

2.1 輪間耦合關系分析

驅動輪通過懸架固定于車架，車輛行駛時某車輪驅動力通過車架傳遞給其它車輪，各驅動輪互相拖拽，產生耦合力。驅動輪的縱向受力分析，如圖1所示。

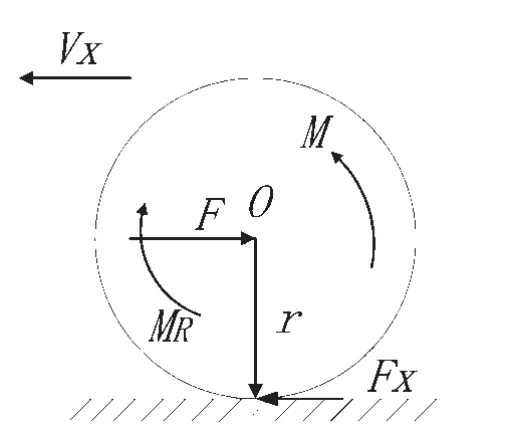
圖1 驅動輪受力分

圖1中，O為車輪滾動中心，r為車輪轉動半徑，Vx為汽車縱向速度，F為作用于車輪軸的縱向力，Fx為地面對車輪的切向作用力，M為車輪驅動轉矩，MR為車輪滾動阻力矩。

車輪縱向力和力矩平衡方程為：

式中，J為驅動系統折算到車輪的轉動慣量，ω為車輪轉速，m為車輪及其簧載的總質量為車輪縱向加速度。

分析電機原理，電機轉矩方程為：

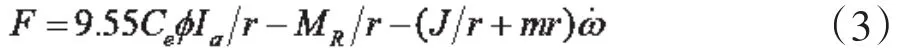
由此，定義F為其余車輪的作用力通過車架傳遞給目標驅動輪的力，F對目標驅動輪的影響即驅動輪輪間耦合問題。

2.2 耦合力F對車輛行駛的影響

當汽車行駛方向與某驅動輪的F值相同時，驅動輪的驅動力系數偏小，車輪滑移率偏小，附著裕度偏大；當汽車行駛方向與F值相反時，驅動輪的驅動力系數偏大，車輪滑轉率偏大，附著裕度偏小[6]。當汽車在爬坡或急加速工況時，驅動力系數最大的驅動輪會最先出現滑轉，從而導致四輪驅動不能達到最大驅動效果，由此增加功率損耗，甚至會影響汽車行駛的穩定性。

由于汽車在坡道、加/減速、轉向情況會發生載荷轉移，當F趨近于0或等于0時，4個驅動輪驅動力系數基本相同，均處于最好的附著條件，由此最大限度地利用垂直載荷較大的輪胎附著圓，增大了汽車的行駛穩態裕度。汽車行駛時，由于內外側車輪產生縱向力之差，從而形成橫擺力矩，可以提高車輛轉向時的操縱穩定性。

3 驅動輪理想轉矩求解

3.1 目標函數與約束條件建立

分析驅動輪輪間耦合關系可得，當四個車輪的F都為0或接近于0時，轉矩分配比較合理。設計基于輪間耦合力最小的驅動力分配目標函數如下：

將耦合力轉化為關于輪轂電機驅動轉矩的目標函數為：

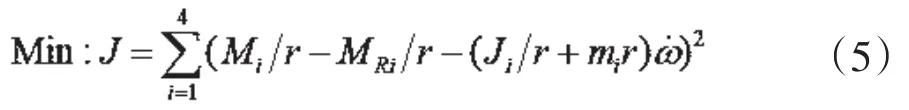
約束條件為：

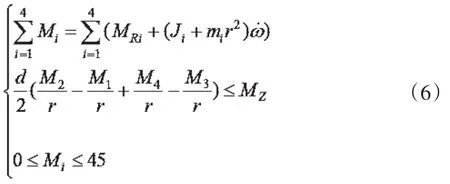
式（4）-（6）中，i為車輪代號。Mi為車輪驅動轉矩，MZ為通過車輛二自由度模型得到的理想橫擺轉矩。

式（6）中，第一項為總驅動轉矩的約束，即總驅動轉矩等于總阻力轉矩。第二項為對左右側車輪驅動轉矩的約束：直線行駛時，使左右側車輪的驅動轉矩相等，即橫擺力矩為0；轉彎行駛時，使左右側車輪的驅動轉矩之差在合理范圍，即產生的直接橫擺力矩不大于車輛轉向所需的橫擺力矩。第三項為對車輪驅動轉矩的約束，使驅動轉矩不大于電機最大輸出扭矩。

3.2 橫擺轉矩MZ確定

約束條件中須確定橫擺轉矩MZ，MZ滿足車輛二自由度轉向動力學模型，如下：

式（7）中，β 為質心側偏角，γ為橫擺角速度，δf為前輪輸入轉角，vx為縱向速度。

在勻速行駛時，前輪轉角階躍輸入下進入的穩態響應即等速圓周行駛，此時，，帶入式（7）可計算得到名義橫擺角速度γd，根據文獻[8]，將理想質心側偏角βd設為0得：

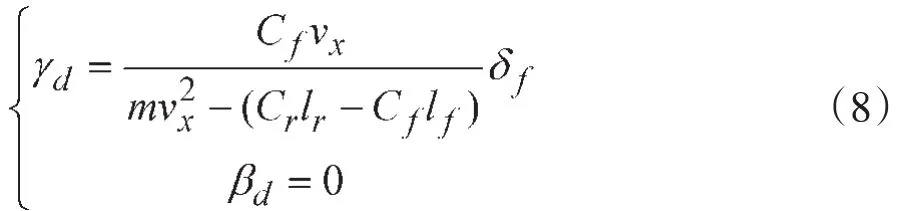
則車輛轉向時的橫擺轉矩為：

目標函數的求解選擇約束條件下多變量尋優，仿真時用Matlab優化工具箱中fmincon函數求解，實驗樣車中應用罰函數法求解。

4 整車控制方法

在整車驅動控制過程中，實際轉矩通過輪轂電機獲取，各驅動輪理想轉矩由驅動力分配方法求得，以最優控制理論為基礎，將實際轉矩與理想轉矩之間的偏差作為控制輸入量，實現對各驅動輪轉矩的控制。驅動轉矩控制實際是對輪轂電機電流的控制，根據四輪驅動力分配方法可以得到在當前狀態下各輪轂電機的理想電流值，再通過反饋調節使各電機的電流值趨近理想狀態[9]。整車控制結構如圖2所示：

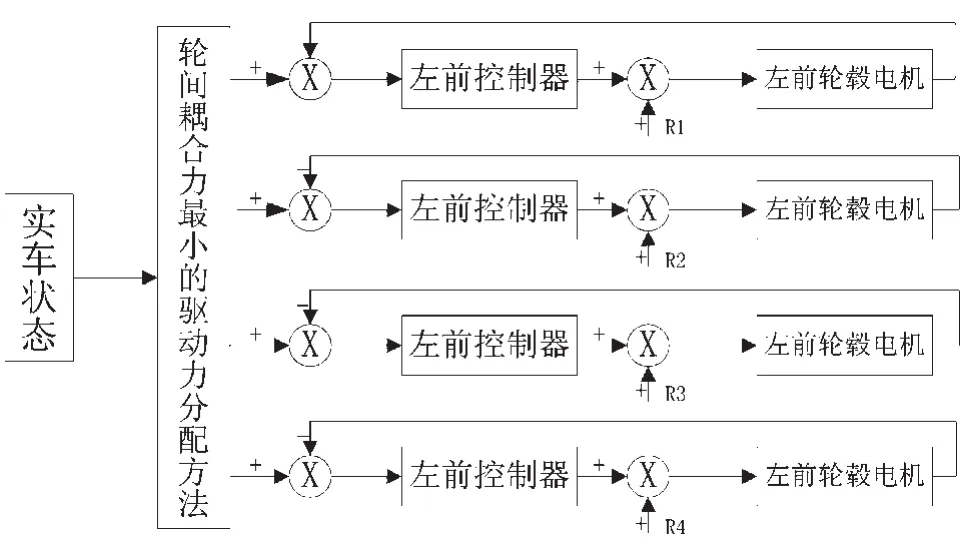
圖2 整車控制結構

5 實車基本參數與ADAMS仿真建模

5.1 實車基本參數

實驗樣車為自行研制的四輪獨立驅動電動汽車，由電源系統、動力系統、轉向系統、制動系統和測控系統組成，通過VC++程序實現信號處理和整車控制[10]。樣車基本參數如表1所示。

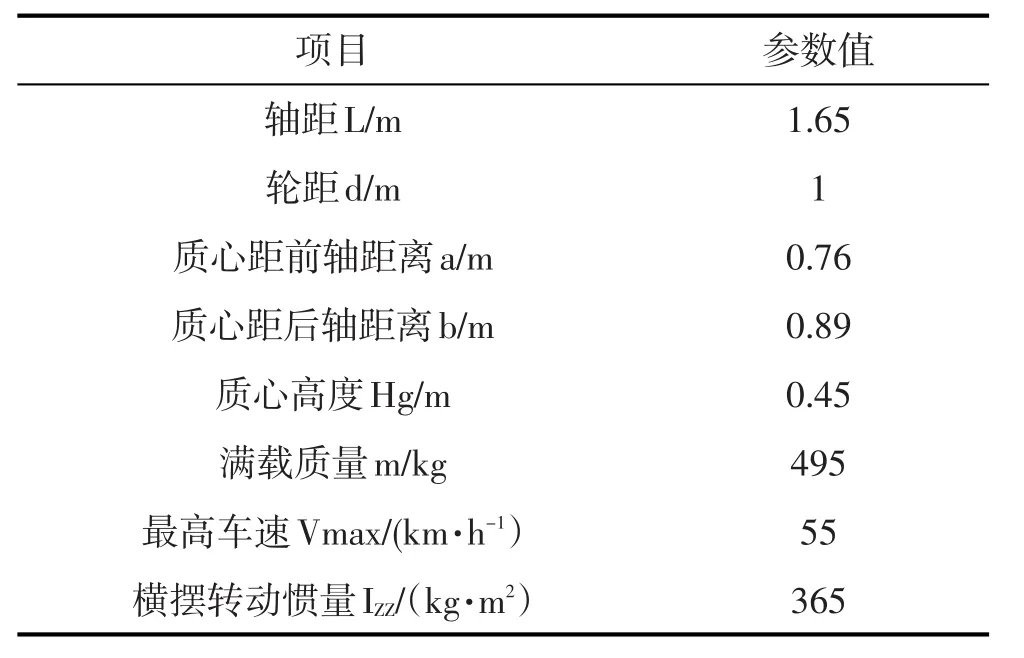
表1 樣車基本參數

5.2 ADAMS仿真建模

為減少建模工作量，重點考慮車輛動力學性能，須先對整車的相關系統和部件進行簡化。然后在ADAMS/View模塊中，以實驗樣車各參數為基礎，結合實際行駛工況，選擇UA輪胎模型和2d_flat地面譜，建立樣車幾何模型。如圖3所示。

圖3 4WID電動汽車ADAMS幾

6 聯合仿真分析

與其他驅動力分配策略相比，基于輪間耦合力最小的分配方法使得相關參量更容易通過傳感器獲得，同時也能得到較好的仿真和實驗結果。本文以基于輪胎利用率最小的驅動力分配方法為例，與本研究方法進行仿真和實驗對比分析。輪胎利用率最小的驅動力分配模型[2]如下：

式中，FX、FY分別為車輛縱向和側向力，C為常系數。

考慮到各不同行駛工況對車輛性能的影響，選擇勻加速變勻速直線和勻速直線變彎道兩種復合工況進行聯合仿真分析。

6.1 勻加速變勻速直線工況

在勻加速變勻速直線工況仿真中，設定車輛加速度為1m/s2的仿真時間為10s，之后保持勻速狀態。圖4為不同驅動方式下耦合力F的仿真結果。車輛直線行駛時，左右側車輪受力情況相同，圖4中只給出左側車輪的仿真結果，其中，實線為左前輪，虛線為左后輪。

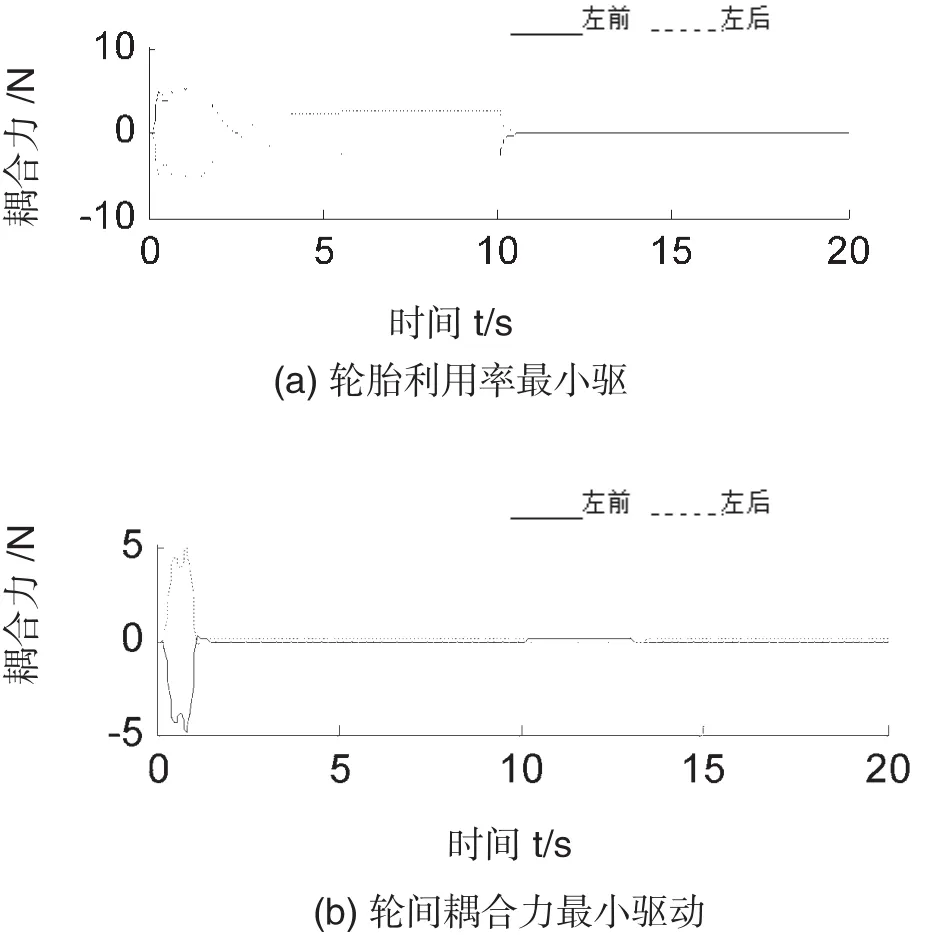
圖4 不同驅動方式下耦合力F的仿真結果

分析圖4（a），輪胎利用率最小驅動時，加速階段耦合力F波動小，勻速階段F接近于0。從圖4（b）可看出，在輪間耦合力最小驅動下，加速階段F只在開始瞬時有小變化，之后包括勻速階F均接近于0。即在這兩種驅動方法控制下，F的變化相似。

圖5為勻加速變勻速直線工況下，上述兩種驅動方式的滑移率仿真結果：

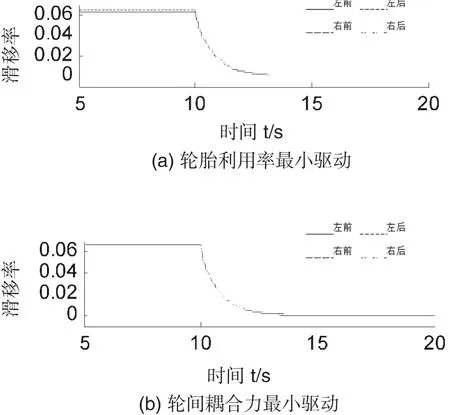
圖5 不同驅動方式下滑移率的仿真結果

如圖5所示，在加速階段，滑移率穩定在0.06，在勻速階段，滑移率平滑過渡，減小到穩定值0.01附近。在該復合工況下，兩種驅動方式的車輪滑移率變化非常相似，即耦合力最小驅動方法也能得到與其他方法類似的滑移率變化。

6.2 勻速直線變彎道工況

在勻速直線變彎道工況仿真中，設定車速為20 m/s，對前輪向左施加2°的轉角，圖6分別為輪胎利用率最小和輪間耦合力最小驅動方式下耦合力F的仿真結果。

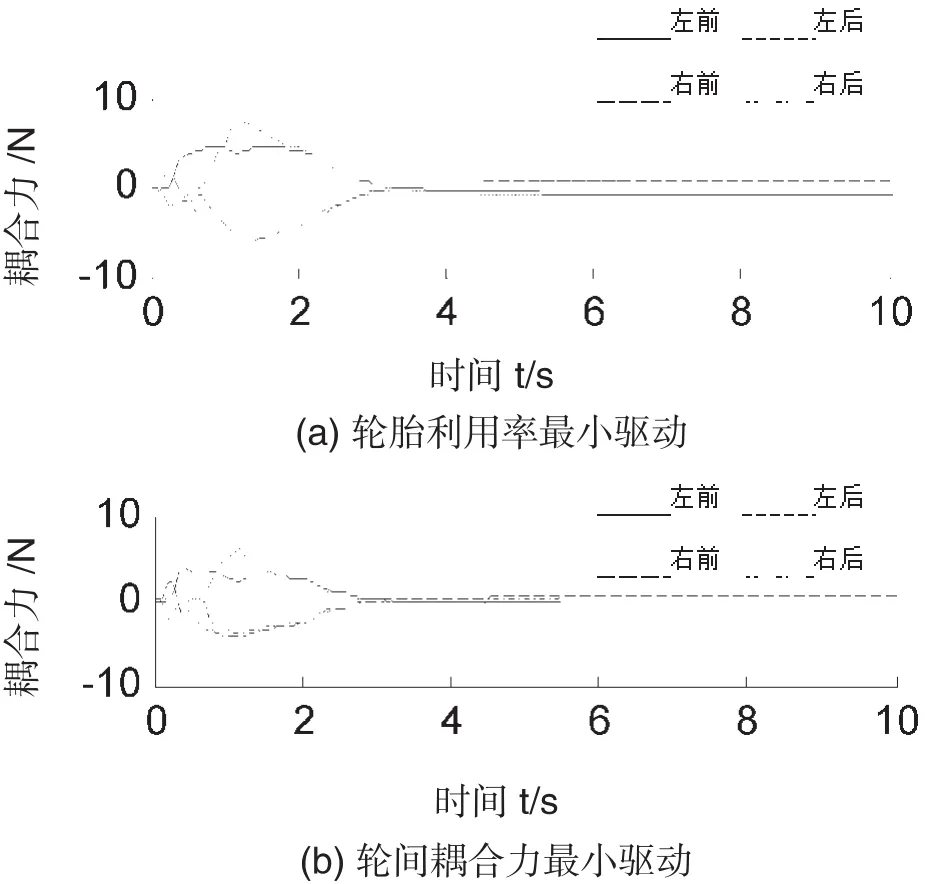
圖6 不同驅動方式下耦合力F的仿真結果

如圖6所示，在該復合工況下，輪胎利用率最小和輪間耦合力最小兩種驅動方式下，耦合力F在勻速階段都出現一定的波動后穩定于0附近。表明在該復合工況下，這兩種驅動方式的F也具有相似的變化趨勢。

圖7為勻速直線變彎道工況下，上述兩種驅動方式的滑移率仿真結果：

圖7 不同驅動方式下滑移率的仿真結果

如圖7所示，在勻速直線變轉彎工況下，輪間耦合力最小驅動與輪胎利用率最小驅動時，車輪的滑移率都相差很小，且變化趨勢都是由開始的小波動趨于一個穩定狀態。表明在這種復合工況下，耦合力最小驅動方法依然能夠得到與其他方法類似的仿真結果。

綜上所述，在勻加速變勻速直線與勻速直線變彎道兩種行駛工況下，進行輪胎利用率最小和輪間耦合力最小兩種驅動力分配方式的仿真實驗，仿真結果表明：兩種模式下的耦合力和車輪滑移率的變化相似，即輪間耦合力最小驅動策略均可以得到較理想的驅動效果。

7 實車實驗

7.1 直線行駛實驗

直線行駛實驗中，實車加速阻力、道路阻力直接影響電機負載，再加上實驗場地路面具有一定的不平度，導致車輪轉速和電機電流的變化趨勢存在相應差異。實驗結果如圖8所示，(a)、(b)、(c)分別為車輪轉速、電機電流及目標與實際電流比對的變化曲線。

圖8 直線行駛實驗曲線

從圖8（a）、8（b）可知，由于車輛加速度不大，載荷轉移不明顯，4個輪轂電機電流基本相同。圖8（c）表明，實際電流變化趨勢與目標值相互吻合，即電機電流在控制器的作用下可較好地跟蹤優化電流值，驗證了電機控制器的合理性。

7.2 轉彎行駛仿真與實驗

受實驗條件限制，圓周行駛實驗只在較低車速下進行。設定車速為4.3 m/s、前輪轉角為0.17 rad，為便于分析，將車輪轉速轉化為車輪質心速度。分別對輪速和電流進行了聯合仿真和實車實驗，結果如圖9、10所示。

圖9 仿真和實驗的輪速變化曲線

圖10 仿真和實驗的電機電流變化曲線

分析圖9、10，在轉彎行駛條件下，仿真與實車實驗的四輪轉速、電機電流都基本吻合。實車實驗的輪速、電流波動是由實驗場地不平引起的，屬于正常現象。

綜上所述，在直線行駛工況下，實車實驗結果驗證了所設計整車控制器的合理性；在轉彎行駛工況下，仿真與實車實驗結果基本吻合，變化趨勢一致。表明基于輪間耦合力最小的驅動力分配方法可以合理的分配4個車輪的驅動轉矩。

8 結束語

（1）通過分析驅動輪輪間耦合關系，建立驅動轉矩目標函數和約束條件，經優化求解，得出基于輪間耦合力最小的各輪理想驅動轉矩。

（2）建立Adams與Matlab聯合仿真模型，以最優控制理論為基礎，設計整車控制器，實現對各驅動輪轉矩的控制，得到整車控制策略。

（3）對比分析聯合仿真與實車實驗結果，在直線和轉彎工況下，實驗與仿真結果吻合，輪間耦合力最小的驅動力分配策略可根據車輛載荷轉移情況合理分配各車輪的驅動轉矩，效果顯著。