基于點云切片技術的曲面擬合方法研究

張開源，鄭德華，張崇軍

（1.河海大學 地球科學與工程學院，江蘇 南京 211100）

三維激光掃描儀是以“面”的測量手段采集點云數據，由于其具有測量精度高、工作速度快、采集信息量大等諸多優點，故而又被稱為“實景復制技術”[1]。該技術能實現迅速、海量獲取三維點云，是測繪領域的一大創新[2]。

三維激光掃描數據處理的結果是通過進行物體表面曲面擬合來建立三維模型。由于獲取的點云是海量數據以及目標物體的形態具有多樣性等特點，使得對該類數據處理難度變大。現有的大部分點云曲面擬合方法擬合得到的結果能夠保留一部分甚至絕大部分的原始點云特征，但有時也會出現局部失真的情況，尤其是對于復雜曲面，從而造成擬合結果精確性不高，影響擬合的效果。此外大部分點云曲面擬合方法的時間復雜度較高，擬合效率較低，尤其是針對包含多種曲面特征的復雜區域，擬合效率更低。為了能夠有效地對點云數據進行處理，引入了數據分割方法。數據分割[3]不僅實現了對點云的分塊和合并處理，而且建立了點云數據間的拓撲結構，為后續整體點云進行分塊曲面擬合提供了便利。

本文首先引入切片方法來對點云數據進行曲面擬合，切片方法通過投影將點云數據實現降維處理，可以克服曲率和法矢變化帶來的部分影響。通過切片處理，將整體點云數據分割成適量切片，能克服復雜曲面的不利影響。然后對基于切片的點云曲面擬合方法進行改進，從多個方向上對切片后的點云進行處理，得到點云擬合區域的擬合數據。為提高整體點云的光滑性，可使用基于移動最小二乘的方法對擬合后數據實現整體光滑處理。該方法保證了點云曲面擬合的質量，保留了更多的原始點云特征，可有效提高點云曲面擬合的精確性。

1 基于切片技術的點云曲面擬合方法

基于切片的點云曲面擬合方法可以分為兩步：切片數據的獲取及投影擬合。對切片數據的獲取，分別采用定寬和自適應切片兩種方法來對點云數據進行處理。對切片的投影擬合，引入移動最小二乘方法來提高切片的擬合精度。同時，提出使用雙向切片法來提升點云曲面擬合的穩定性和可靠性。

1.1 點云切片寬度

在點云數據中，以某一指定方向為法方向，沿該方向設置一個平面族Γ，則某一平面E的表面線即為該平面處的點云切片，其本質為平面E和點云相交后得到的點云區域。在實際應用中，由于各種因素的影響，要嚴格以平面上的點來計算獲取該平面處的點云切片是無法實現的，因此引入“切片寬度”，即將該平面E沿著法方向的兩側各移動相等寬度，生成兩個新的平面El和Er，則兩個新的平面El和Er中間的點云即為該平面所在的點云切片。點云切片寬度的確定是基于切片的點云曲面擬合方法研究的關鍵步驟之一，主要可以分為兩大類：定寬切片寬度的確定和自適應切片寬度的確定。

1.1.1 定寬切片寬度的確定

定寬切片是比較常見的切片獲取方法，它是通過計算獲得切片的寬度，以此寬度為基準對點云數據進行切片處理，獲得許多寬度相等的切片。目前常用的切片寬度計算方法為密度法，通過計算得出點云的密度，然后確定切片的寬度。本文介紹基于空間格網劃分的密度法[4-5]，這種方法是以K鄰點搜索中的空間分塊策略方法為基礎的[6]。根據劃分好的空間包圍盒網格，統計網格中空的包圍盒個數來進行計算：

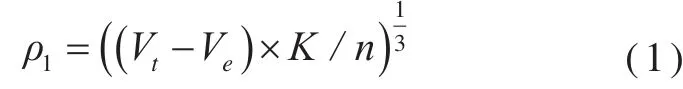
式中，Vt為所有小包圍盒的個數；Ve為所有空的小包圍盒的個數；K為鄰近點的個數；n為點云的總數。

根據公式求解點云數據密度，進一步求解切片寬度：

式中，k1為經驗系數，一般取值4～8。

1.1.2 自適應切片寬度的確定

定寬切片處理得到的切片寬度是一樣的，適用于曲率變化小的平緩點云或平面點云。對于曲率變化較大或局部密度不均勻的區域，如果仍使用定寬切片的處理方法，得到的切片進行投影之后，就會出現厚度相差較大的情況，會對后續擬合產生重大影響，進一步影響到點云曲面的擬合。因此，本節引入一種自適應的切片獲取方法，通過對切片投影厚度的控制，來調節切片的寬度，得到寬度不等的點云切片數據。自適應切片方法的主要思想是：

1）首先確定自適應處理過程中一些基本變量，例如以沿X軸為切片方向，則取最小值和最大值Xmin、Xmax作為切片的起止點。設切片的初始寬度為ΔX，這個初始寬度可以通過密度法計算得到。

2）在X1=Xmin時作為第一個切片平面，根據計算得到切片的初始寬度△X，則在X2=X1+ΔX時取第二個切片平面，兩個平面之間的數據即為第一個切片數據。

3）將第一個切片數據投影到切片平面上，得到切片投影數據，判斷切片投影數據的最大厚度是否超過設定的閾值。若超過設定的閾值，則進入到步驟（4）；若沒有超過，則進入到步驟（5）。

5）比較X2是否超過Xmax，如果超過Xmax，則令X2=Xmax，進入步驟（6）；如果沒有超過Xmax，則令X1=X2，X2=X1+ΔX，重復步驟（3）中的操作。

6）提取切片數據，處理完成。

1.2 切片擬合

點云切片數據的投影擬合是基于切片的點云曲面擬合方法的另一個關鍵步驟，根據切片處理方法得到點云的切片數據，對切片數據進行投影處理，然后擬合投影數據。本文引入了移動最小二乘法[7-9]（moving least square，簡稱MLS）來對切片的投影數據進行擬合。首先求出切片數據中每個數據點的緊支撐域，選取合適的權函數和基函數后，根據相應公式即可求出擬合后的數據。基于MLS法的擬合方法，通過選取不階基函數和權函數得到不同的精度和光滑度，能夠在一定程度上克服最小二乘法適用于數據量不大、切片形狀簡單的情況，但對于線形復雜、數據量較大的切片數據，則需要進行分塊擬合。

1.3 基于雙向切片技術的曲面擬合

在利用切片技術進行曲面擬合時，單一方向的切片方法能在一定程度上滿足點云數據曲面擬合的需要。大量的實驗表明，不同方向的切片得到的擬合數據效果不同。在對實驗對象做切片處理時，求出的最佳切片方向僅僅是針對某一部分數據而言，不存在對所有點云數據的切片效果都最佳的切片方向。

由于不同方向切片的擬合效果具有差異性，不同方向的切片擬合效果具有不穩定性，對多個方向進行切片得到的切片數據具有一定的優勢互補性。本文提出使用一種基于雙向切片優勢互補的點云曲面擬合方法，通過在多個方向上對同一實驗對象做切片處理，得到不同方向的擬合數據。為避免擬合數據過多而造成誤差累積，選取其中擬合效果最好或具有優勢互補效果的兩個方向的數據，然后根據移動最小二乘法原理，采用穩健光滑方法對兩個方向的擬合數據進行去噪光滑處理，可得到最終的擬合數據。具體算法流程如下：

1）對待擬合點云數據進行多方向切片擬合處理，根據條件選擇其中擬合效果最好或具有優勢互補的兩個方向切片數據，使用移動最小二乘法進行整合處理；

2）將原始點云數據和整合后的點云數據進行比較和計算，得出擬合后點云數據中每個數據點的殘差Vi以及中誤差σ；

4）利用剩下的點重新計算，循環執行（2）～（3）環節，直至所有點的誤差都在要求范圍內為止；

5）利用移動最小二乘法對最終得到的點云數據再次進行光順處理，即可得到最佳擬合結果。

相比于最小二乘法而言，移動最小二乘法的擬合函數構造相對簡單，由于引入緊支撐域，能有效提高擬合數據的光滑度，且穩健過程能有效剔除擬合過程中產生的粗差，保證了最終的擬合精度。

2 實驗案例及分析

使用Trimble GX型號三維激光掃描儀對石質雕像進行測量，得到點云數據，對預處理過的數據進行分割，獲得石質雕像的點云數據。由于雕像表面凹凸不平，毫無規則，所以選取整塊雕像點云數據進行實驗和選取部分雕像點云數據進行實驗效果類似，為方便后續的實驗對比，在聚類分割后的某一區域中截取一部分具有代表性的點云數據進行實驗。

截取點云及其附近數據共5 768個，然后提取點云數據的外邊界數據步驟為：①取K值為30，進行K鄰點搜索；②計算數據點的法矢，并對其做方向一致性調整；③根據點云數據邊界探測度量原則探測點云數據的邊界點；④使用旋向法對點云數據的外邊界進行提取，得到點云數據的外邊界數據。

對點云數據使用三次多項式擬合方法做擬合處理，得到函數為：

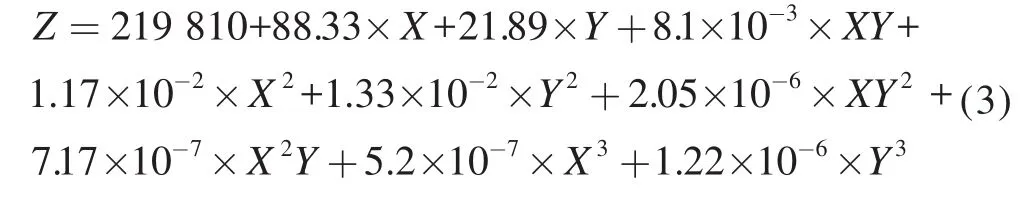
根據曲面函數對點云曲面數據及其附近數據進行內插計算得到插值數據，再根據邊界數據對點云曲面擬合數據進行提取，得到擬合數據共2 479個（見圖 1）。

使用基于切片的點云曲面擬合方法對點云曲面進行擬合，主要有定寬切片方法和自適應切片方法。使用基于自適應切片（X方向）的點云曲面擬合方法對點云數據進行切片、擬合處理得到切片擬合數據，得到33條切片數據、擬合數據5 380個（見圖2）。使用密度法計算得到點云定寬切片的寬度為12.5 mm，使用基于定寬切片（X方向）的點云曲面擬合方法對點云數據進行切片、擬合處理得到切片擬合數據，得到48條切片數據、擬合數據2 357個（見圖3）。

基于雙向切片優勢互補的曲面擬合方法，在多個方向上對同一實驗對象實現切片化，選取其中優勢互補的兩個方向（本實驗使用X、Y軸兩個方向進行處理）上的數據，使用穩健移動最小二乘方法進行綜合處理，得到最終的擬合數據共8 736個（見圖4）。

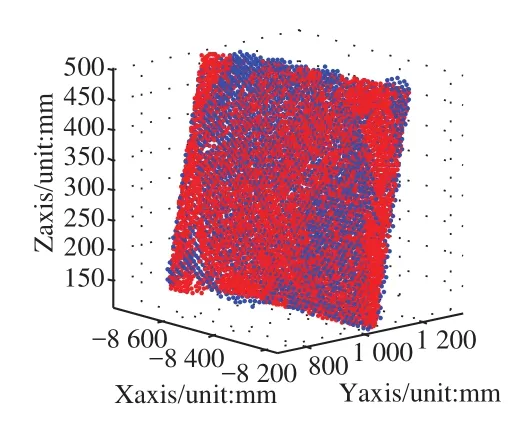
圖1 基于多項式方法的點云曲面擬合效果圖

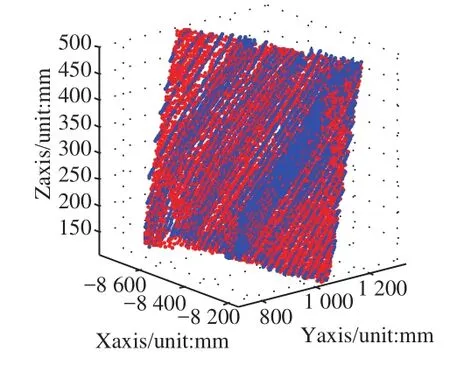
圖2 基于自適應(X方向)切片的點云曲面擬合效果圖

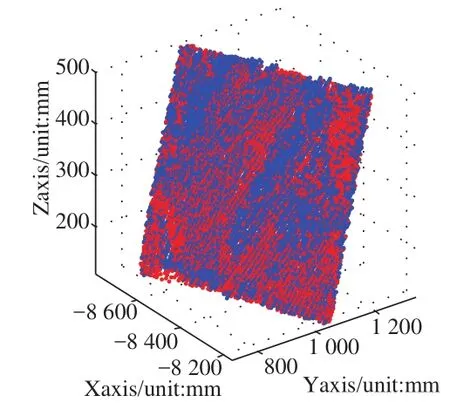
圖3 基于定寬(X方向)切片的點云曲面擬合效果圖

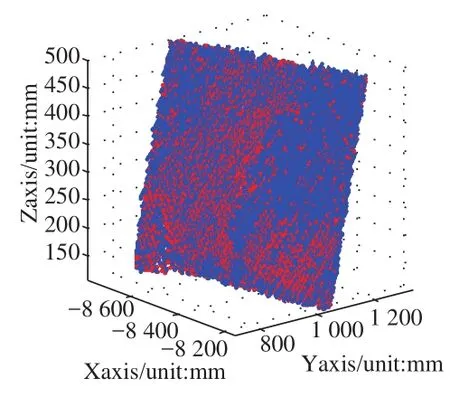
圖4 基于雙向切片優勢互補的點云曲面擬合效果圖

將本文使用的點云曲面擬合方法所得到的擬合效果進行整理，以使用最普遍的多項式曲面擬合方法為參照對象，將其他方法得出的結果與其比較，計算各方法提升的精度百分比（見表1）。

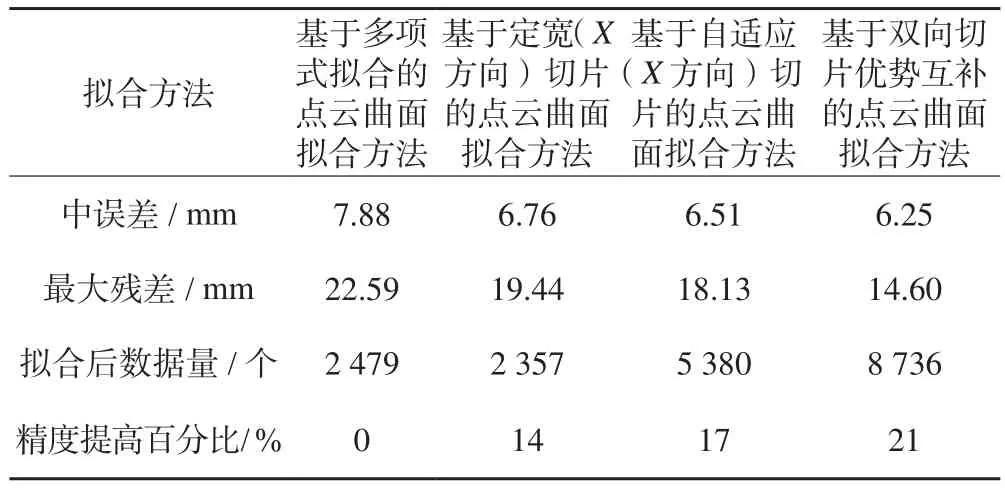
表1 不同點云曲面擬合方法擬合效果對比表

以散亂無規則、表面凹凸不平且分布不均勻的點云數據進行實驗，從以上各種方法的效果圖可以看出，這些方法的擬合數據能夠覆蓋原始點云曲面區域，滿足點云曲面擬合的要求，根據實驗得到如下結論：

1）對比不同點云曲面擬合方法的擬合效果，面對表面情況復雜、密度不均勻的點云，非切片法曲面擬合效果一般，切片法擬合效果明顯優于非切片法擬合效果，非切片方法法擬合的中誤差在6.99～7.88 mm，最大殘差在21.26～22.59 mm。切片方法擬合的中誤差在6.25～6.76 mm，最大殘差在14.60～19.44mm。由擬合的效果可以看出，對含有多種曲面特征的點云曲面數據進行擬合，基于切片的點云曲面擬合方法優于其他方法。

2）基于定寬（X方向）切片擬合的中誤差為6.76 mm，最大殘差為19.44 mm。基于自適應（X方向）切片擬合的中誤差為6.51 mm，最大殘差為18.13 mm。自適應切片能夠根據點云曲率和厚度的變化合理地進行切片處理，由擬合的效果可以看出基于自適應切片的方法優于基于定寬切片的方法。

3）基于雙向切片優勢互補的擬合方法的中誤差為6.25 mm，最大殘差為14.60 mm。使用單向切片方法對點云曲面擬合的效果具有不穩定性，因此本文提出使用雙向切片優勢互補的方法來提高點云曲面擬合的穩定性。由擬合的效果、擬合后數據量及精度提升百分比可以看出，基于雙向切片優勢互補的點云曲面擬合方法明顯優于單向切片方法。

3 結 語

使用單向的點云切片方法能夠快速、高效地對點云曲面數據進行擬合，由于切片方向不是唯一的，造成點云曲面擬合效果存在不穩定性。本文提出了一種基于雙向切片優勢互補的點云曲面擬合方法，選擇擬合效果最好或具有優勢互補效果的兩個方向的數據，利用移動最小二乘方法進行穩健光滑處理來獲得最終的擬合數據。根據實驗結果分析，相對于多項式擬合方法、單向切片方法，基于雙向切片優勢互補的點云曲面擬合方法在精度和穩定性方面均有了明顯提升。但本文主要對雙向切片方法進行了研究，在今后的工作中，可以進行深入研究一種基于三維空間特征方向或者更多方向的切片方法來提高點云曲面擬合結果的穩定性和可靠性。