關于幾個典型的剛體運動問題中被動力作用的教學討論
崔乃毅 米儀琳 孫連亮 李春磊 毛志國
(北方工業大學理學院,北京 100144)
被動力存在于有約束的物體運動問題中。例如,滑動摩擦力和靜摩擦力,軌道對質點的約束力等。在剛體的有軸轉動中,軸對剛體的約束力也是被動力。相對質點運動問題,被動力的存在在剛體運動問題中更不易直觀。教學中,忽視對這一問題的講解可能導致學生錯誤地理解剛體運動甚至錯誤地求解問題。本文結合幾個典型習題,就剛體碰撞中的被動力問題做一些討論。
1 小球撞懸掛桿問題
這是一類典型的被動力問題,這類問題的最普遍的教學難點是總有相當比例的學生不理解此類碰撞中動量為何不守恒,而錯誤地對小球-桿二體系統用動量守恒定律求解[1]。教學中,一般是討論整個小球-桿二體系統在碰撞中的動量變化來說明這一問題,但過程相對繁瑣[2,3]。而討論桿的懸掛軸處的被動力會使問題變得簡化,同時也直接切入了該問題中動量不守恒的關鍵[4]。為此,只把桿納入討論即可,把小球對桿的碰撞簡單表示為一個沖量。設勻質細桿的質量為M,長為L,無摩擦懸掛軸距桿的中點(質心)C的距離為x。初始時桿靜止于豎直方向,一大小為I的水平沖量作用于桿的下端(見圖1(a))。
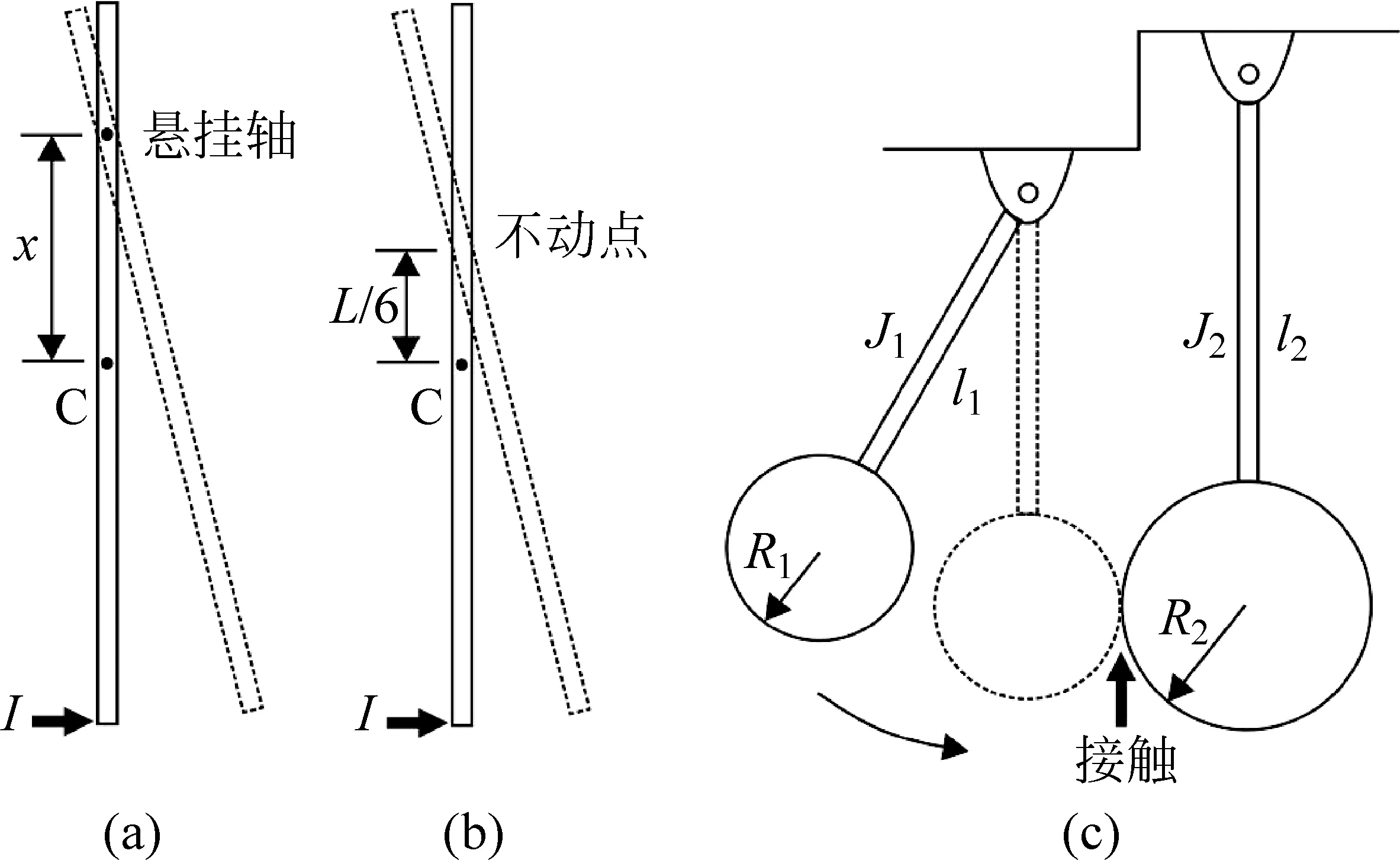
圖1 小球-桿二體系統(a)小球與懸掛桿碰撞;(b)小球與自由桿碰撞;(c)剛體擺碰撞問題的一個例子
為使描述盡量簡單以便于學生理解,僅討論水平方向的動量。學生一般認同使用關于懸掛軸的角動量定理求解這一碰撞過程,因此仍使用這一方法。這里略去推導過程,很易得到碰撞后桿繞軸的角速度如下:
(1)
這里轉動正向為逆時針,沖量正向向右。再利用碰撞后的瞬間桿的質心速度公式vC=ωx,即得懸掛軸對桿的沖量Ip=ΔMvC-I
(2)
顯然,此式并不永遠為零,表明碰撞中懸掛軸對桿確實施加了水平作用力,使小球-桿二體系統的動量發生變化。該力的沖量即由該式定量計算。式(2)還指出,決定Ip的值和指向的最重要因素是懸掛軸在桿上的位置x,并且依x不同,Ip可能向右,也可能向左。當Ip向右時,小球和桿的二體系統的總的水平動量增加,反之減少。至此,學生已經能夠理解為何該碰撞過程動量是不守恒的。
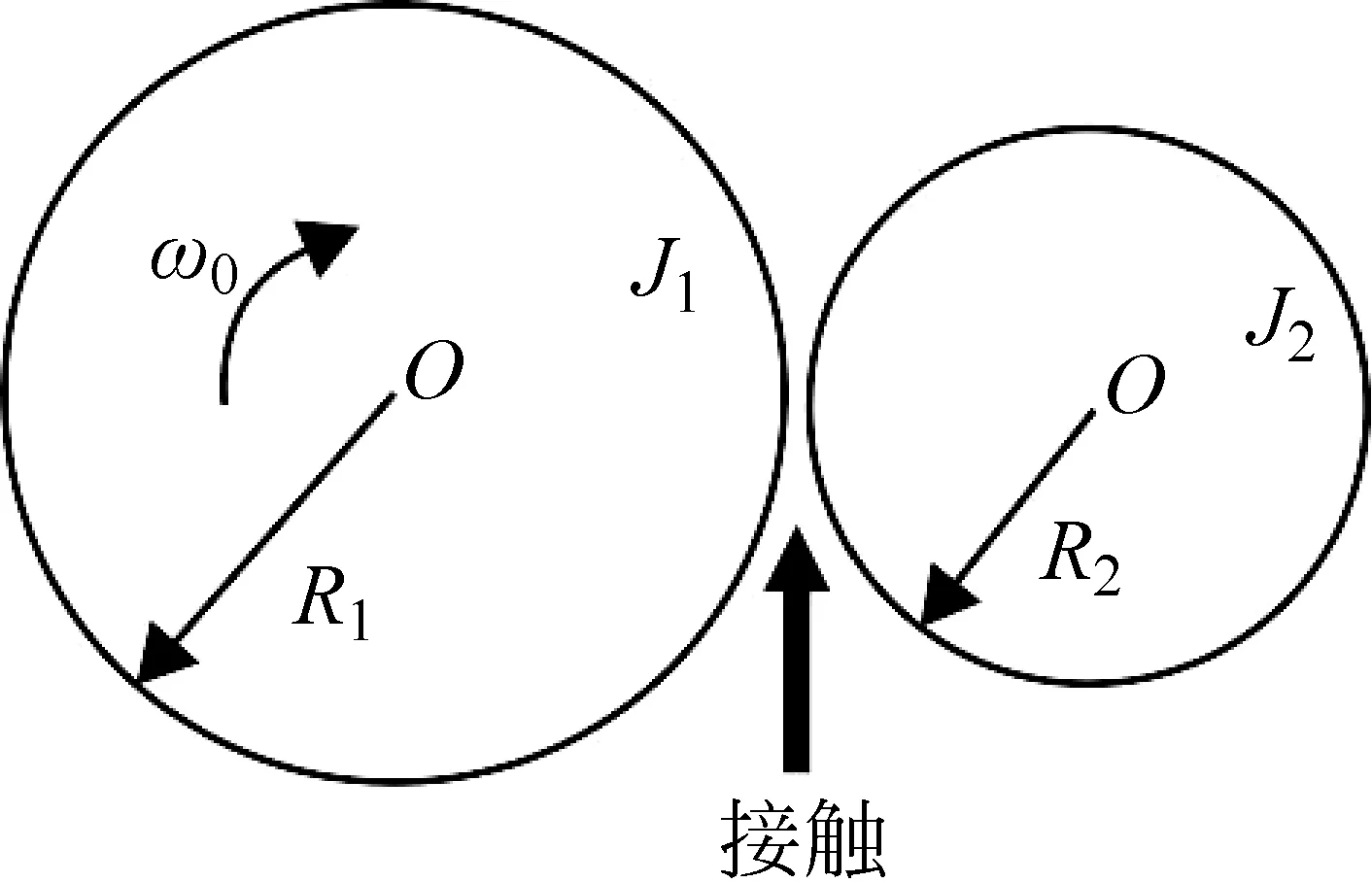
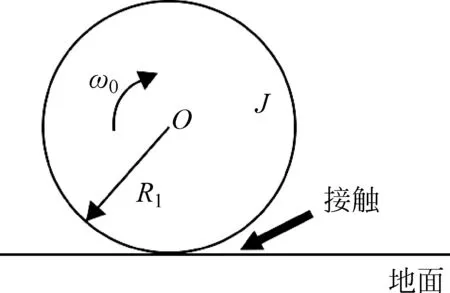
從由式(2)確定的Ip/I隨x/L變化的函數曲線(見圖2)可以清楚地看到,在x>L/6區間,Ip>0,與I同向,碰撞后二體系統的總水平動量增大;在x x=L/6 (3) 時,Ip=0,表明此時懸掛軸對桿沒有水平力。只有當懸掛軸選在這一點時,小球-桿二體系統同時滿足水平方向的動量守恒和關于懸掛軸的角動量守恒條件。可見,這一碰撞問題中體系動量守恒與否只與懸掛軸在桿上的安裝位置有關,與小球和桿的質量、小球與桿之間的碰撞是彈性或非彈性等因素均無關。 圖2 小球撞懸掛軸問題中懸掛軸對桿的被動力沖量Ip與軸的位置的關系,圖中橫軸為比值x/L,縱軸為比值Ip/I 另兩個特殊點是x=0和x=L/2,前者是把軸安裝在桿的中點,此時由式(2)得Ip=-I,碰撞中桿受到的水平總沖量為零,質心不動,碰撞傳遞給桿的動量全部被Ip抵消,I的作用只是對桿產生了繞質心C的轉動。后者是懸掛軸處于桿的上端。這時由式(2)得到碰撞中軸對桿的沖量為Ip=I/2,二體系統向右的總水平動量增加了I/2。 前面討論的問題與小球與無懸掛點的自由桿的碰撞問題密切相關。如圖1(b),如沿水平面在桿的一端沿垂直于桿的方向敲擊靜止放置于光滑的水平面上的勻質細桿,則敲擊前后桿上保持不動的點的位置(轉動瞬心)即為距桿的中心x=L/6處。 圖3 摩擦輪問題 如圖3,兩摩擦輪半徑分別為R1和R2, 其繞過中心且垂直于輪面的光滑軸的轉動慣量分別為J1和J2。輪1以角速度ω轉動,輪2靜止不動。如將兩輪邊緣接觸,則摩擦將使輪2轉動起來,直到最后接觸點處兩輪線速率相同因而兩輪間不會再存在滑動[5]。該過程中,如果轉動軸不存在,兩輪接觸后接觸點處的作用力將使兩輪分別向圖中的上方和下方飛走。而轉動軸的存在制止了這種運動。因此轉動軸處必存在被動力。設接觸點處摩擦力的總沖量的大小為I,由角動量定理,對兩輪分別有 (4) 式中ω1和ω2分別為兩輪接觸后接觸點處滑動消失后兩輪各自的角速度,它們之間滿足關系式ω1R1=ω2R2。利用此式可在式(4)中消去兩個角速度得到I的表達式: (5) 式(5)表明,只要ω0≠0,則兩軸處必有被動力。這個沖量的產生要求接觸點處存在滑動摩擦。但沖量值并不與摩擦系數有關。 圖4 剛體摩擦加速問題 見圖4,將一個質量為M轉動慣量為J,半徑為R,以角速度ω0旋轉的輪子保持豎直并緩慢地放到非光滑的地面上,接觸點處的被動力將使輪子加速,直至最后進入純滾動狀態。整個摩擦加速過程被動力f的總沖量可以如下求得。圓盤的平動速度v和轉動角速度ω應滿足的動力學方程分別為 此處J為圓盤的轉動慣量。將兩方程聯立消去f后所得到的新方程兩邊可對整個加速過程積分,取積分上、下限分別為初始條件和純滾動條件ω=v/R,即 (6) 由式(6)解出v=ω0R/(1+MR2/J)。此即為純滾動發生后圓盤的滾動速度。圓盤獲得這一速度的唯一原因是接觸點處的力,因此這一過程中接觸點處的被動力的沖量即為圓盤質心獲得的動量: I=Mv=Mω0R/(1+MR2/J) (7) 與前一個問題類似,這個沖量的產生也要求接觸點處存在滑動摩擦,而沖量值與摩擦系數也無關。如果圓盤是勻質的,可把轉動慣量J=MR2/2代入結果,得到I=Mω0R/3。 以上對幾個實例通過求被動力的沖量討論了被動力在分析剛體動力學問題中的作用。涉及被動力的剛體力學問題很多。使學生正確理解和求解這類問題的關鍵是要說明有約束和無約束時剛體運動的不同是因為約束對剛體施加了力,即被動力。即約束是通過力作用于剛體的。比如在問題一中,如果學生定量計算出了懸掛軸施于桿的力的值,則很易理解桿的動量為何不守恒。因此,在研究剛體運動過程中決不能忽視被動力的存在,否則導致錯誤地求解問題。而這正是在目前大學物理教學中的薄弱環節。在分析力學中,可以用更加嚴密、更為快捷的辦法計算約束力。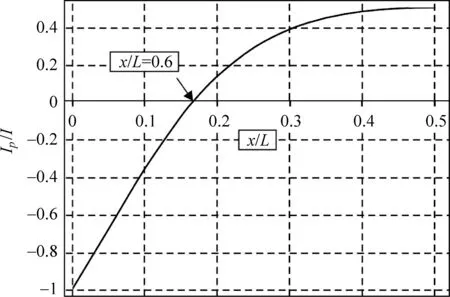
2 摩擦輪問題
3 剛體摩擦加速問題
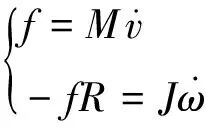

4 結語

