基于優化FOA-BPNN模型的脫貧時間預測

朱容波，張靜靜，李媛麗，海夢婕，王德軍

(中南民族大學 計算機科學學院，武漢430074)

二十世紀中期以來，國際社會和各國政府致力于解決貧困問題.中國政府和人民經過多年探索實踐找到一條具有中國特色的減貧道路——精準扶貧戰略思想[1].目前，精準扶貧的相關研究主要集中在理論層面的定性分析以及運用信息技術對精準扶貧工作進行管理[2, 3].缺乏對脫貧的深層次原因和機理進行精確定量分析的模型和方法[4].

神經網絡由于具有自學習[5]、聯想存儲與高速尋優能力[6,7]，在非線性問題分析與預測方面得到了廣泛應用[8]：利用神經網絡和回歸樹對肝癌患者的生還率進行預測[9]、構建乳腺癌分類預測模型[10]等.相比于粒子群優化等群智能算法，果蠅優化算法(Fruit Fly Optimization Algorithm, FOA)因其參數簡單而為人們所接受[11].FOA中果蠅通過與相鄰個體交換信息，向味道濃度最高的個體聚集；食物到達視覺范圍后，準確飛向目標[12].FOA具有較強處理復雜優化問題的能力且易編碼實現[13].

為了對扶貧的成效與脫貧時間等因素進行準確刻畫與定量分析，本文引入具有自學習以及尋優能力強的神經網絡，實現脫貧時間的有效預測.并針對BP神經網絡模型可能陷入局部最小的缺陷，引入果蠅優化算法對BP神經網絡的參數選擇進行改進，形成FOA-BP神經網絡預測模型.以BP神經網絡的預測誤差作為適應度值，尋找最優的BP神經網絡參數值，提高預測精度.在標準果蠅優化算法中引入動態變速因子和種群密度，調節種群在不同搜索階段的間隔步長，提高果蠅種群的收斂速度和精度.

1 基于DSFOA-BPNN的脫貧時間預測

1.1 問題描述

針對不同的貧困戶個體，如何對扶貧政策進行合理的配置，才能使貧困戶在最短的時間實現脫貧？該問題可以表述為圖1所示的優化問題：以貧困戶的敏感屬性以及政策組合作為輸入，輸出貧困戶的脫貧年限.

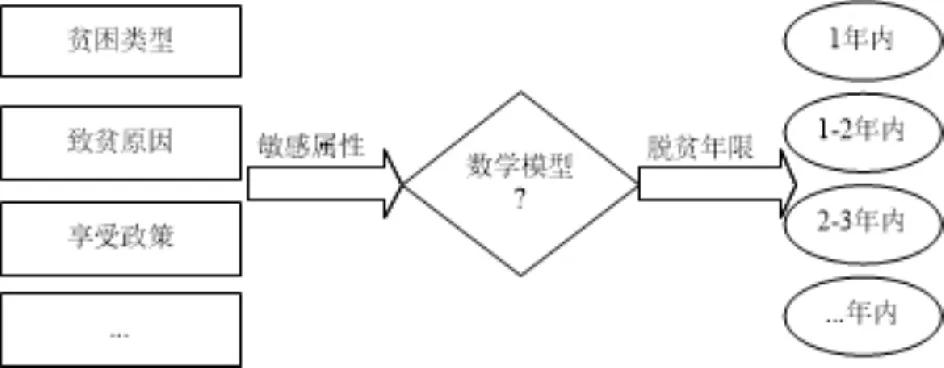
圖1 問題描述Fig.1 Description of the problem

通過對入庫貧困戶相關基本信息進行整理，提取貧困戶的貧困戶類型(T)、致貧原因(R)、子女數(C_n)、耕地面積(A)、技能程度(B)以及享受的政策等敏感信息(C)作為模型的輸入X；抽取貧困戶的入庫日期以及脫貧日期，計算貧困戶從入庫到脫貧所用的時間即脫貧年限Y，即Y={y1,y2,y3,…,ym}作為模型的輸出，構建脫貧時間預測模型，其框架如圖2所示，包括數據預處理模塊和預測建模模塊.

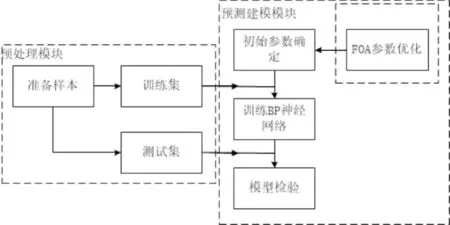
圖2 模型框架Fig.2 Model framework

數據預處理模塊將已脫貧與未脫貧貧困戶進行分離，利用Python對已脫貧貧困戶數據表中冗余項、缺失項進行刪除填充操作，將貧困戶的貧困戶類型、致貧原因、以及享受的政策進行one-hot編碼.同時對已脫貧貧困戶數據進行分割，形成測試集與訓練集.

預測建模模塊的核心是利用BP神經網絡構建的分類預測模型，該模型旨在利用訓練集數據進行多次訓練，對模型參數反復調整，直至模型的準確率達到預期效果.在建模過程中需要確定BP神經網絡的輸入層節點數、隱層數及隱層節點數、輸出節點數、初始權重閾值、學習率等相關參數.考慮到BP神經網絡的初始參數選擇不當可能會導致模型的準確率降低，本文提出了改進的果蠅優化算法實現初始權重和閾值選擇，提升模型的預測準確率.

1.2 動態步長果蠅優化算法

果蠅群體搜尋食物的過程可看作解決優化問題的過程，抵達食物的個體代表問題的可行解.其中標準果蠅優化算法具體步驟[13]如下：

步驟1：定義果蠅種群規模為Size，種群迭代尋優的最大迭代次數Maxg，當前迭代步數g，果蠅種群的初始位置(X_axis,Y_axis)，初始搜索步長R0；

步驟2：確定果蠅個體搜索步長R，根據果蠅群體的初始位置隨機生成果蠅個體i的位置坐標(xi,yi)；

步驟3：計算個體當前位置離原點的距離dist(i)，取其倒數S(i)作為氣味濃度的判定值；

步驟4：通過適應度函數Function()計算果蠅個體i的適應度值Smelli；

步驟5：找出本次迭代氣味濃度最高的果蠅個體，記錄該個體的編號bestIndex與位置坐標(xbestIndex,ybestIndex)以及氣味濃度信息bestSmell；

步驟6：比較當代最優氣味濃度是否高于上一代，若是則執行步驟7，否則返回步驟2；

步驟7：更新種群的初始位置(X_axis,Y_axis)，保留當前最高的氣味濃度值SmellBest；

步驟8：判斷迭代次數是否達到最大值，若是則算法結束，否則回到步驟2.

由上述步驟可知果蠅優化算法(FOA)的收斂精度和搜索速度與搜索步長有密切關系.在傳統FOA中，搜索步長R為定值，可能導致初期迭代尋優搜索范圍過小，難以在規定迭代時間內獲得最優解；或迭代后期R偏大，種群無法精確找到最優解.為避免上述情況發生，對算法的搜索步長進行動態調整，保證果蠅群體在尋優的不同階段獲得合適的搜索半徑，提高搜索精度.

動態步長果蠅優化算法(DSFOA)在步驟2中利用變速因子和種群密度動態調整搜索間隔，搜索步長表達式如下:

(1)

其中，變速因子α描述相鄰迭代最優氣味濃度變化引起的搜索間隔變化程度；bestSmelln為第n次迭代最優氣味濃度.當α>0時，降低搜索步長提高局部尋優能力；當α<0時，增大搜索步長，擴大搜索范圍.本文引入種群密度ρ，理想情況下，搜索前期種群密度偏小，保證種群的多樣性，提高搜索速度;搜索后期種群密度偏大，提高局部尋優能力；迭代次數越大，種群密度對步長的影響越小.

(2)

(3)

DSFOA其他步驟同FOA，由于DSFOA在搜索過程中通過α和ρ調節搜索速度和范圍，在加快種群靠近目標的同時，提升了搜尋范圍的精準度，對算法的復雜度沒有太大影響.

1.3 基于DSFOA的BP神經網絡模型

利用果蠅優化算法對BP神經網絡的的初始參數進行尋優，構建基于果蠅優化算法的BP神經網絡模型(Fruit Fly Optimization Algorithm BP Neural Network, FOA-BPNN)，在一定程度上提高BP神經網絡的預測精度.其算法流程如圖3所示.

基于動態步長果蠅優化算法的BP神經網絡模型(Dynamic Step Fruit Fly Optimization Algorithm BP Neural Network, DSFOA-BPNN)是在FOA-BPNN的基礎上，將左側FOA替換為本文提出的DSFOA，利用DSFOA對BPNN的初始參數進行一定程度的優化.

DSFOA-BPNN算法詳細步驟為：

1)選擇原始數據作為樣本數據，進行歸一化等相關數據預處理；

2)確定BPNN拓撲結構形式和相關參數；

3)執行動態步長果蠅優化算法.在本次實驗中，將果蠅個體作為參數可行解應用到BP神經網絡，并對測試樣本集進行預測得到均方根誤差，以此作為動態步長果蠅優化算法步驟4(同FOA步驟4)中果蠅個體的適應度值，即氣味濃度.因此個體i適應度函數Functioni表示如下：

(4)

其中n為測試樣本數量;Oobs,j與Omod,j分別表示實例值與網絡輸出值.

4)將步驟3)中得到的權值和閾值賦予BPNN進行訓練，利用優化算法對BP神經網絡權重與閾值進行調節.

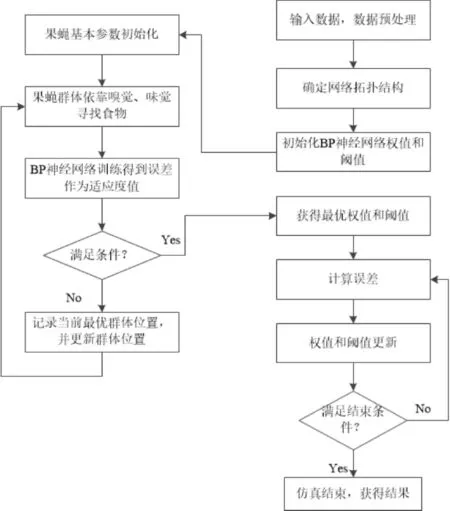
圖3 FOA-BPNN算法流程圖Fig.3 Flowchart of FOA-BPNN algorithm

2 實驗結果

2.1 實驗設置

實驗硬件環境為：Ubuntu14.0 64位系統，利用Python的集成開發環境Jupyter實現數據預處理操作及果蠅優化算法，借助Tensorflow深度學習框架構建神經網絡.本研究收集了某貧困地區在2014～2016年間脫貧的貧困戶數據共95000條，依據貧困戶的脫貧時間將數據分為3類，即脫貧時間為2014年、2015年、2016年，數據量分別為21640、42850、30510.按照4∶1的比例對預處理后的數據進行均勻分割，形成訓練集與測試集.

模型輸入包括貧困戶類型(T)、致貧原因(R)、享受的政策等敏感信息(C)等26項，則模型輸入層節點數為26；與3個脫貧時間段相對應，輸出層節點數為3；根據經驗公式(5)確定隱層節點數為6.

(5)

其中Nin，Nh，No分別表示輸入層、隱層、輸出層的結點數，α為正整數，且0≤α≤10.

為了綜合下降算法和隨機梯度下降算法的優缺點，實驗中每次只計算一小部分訓練數據的損失函數，這一小部分數據被稱為一個batch.通過矩陣運算，每次在一個batch上優化神經網絡的參數并不會比單個數據慢太多.利用指數衰減法設置學習率并使用L2正則化避免過擬合問題，限制權重大小使模型不能任意擬合訓練數據中的隨機噪音.

對于動態步長果蠅優化算法部分，設置種群規模Size為30，最大迭代次數Maxg為300.每一個果蠅個體的維度為D，其表達式為：

D=NinNh+NhNo+Nh+No.

(6)

2.2 實驗結果及分析

經過訓練集數據訓練后，3種方法對脫貧時間的預測準確率與損失函數值的變化曲線如圖4所示.

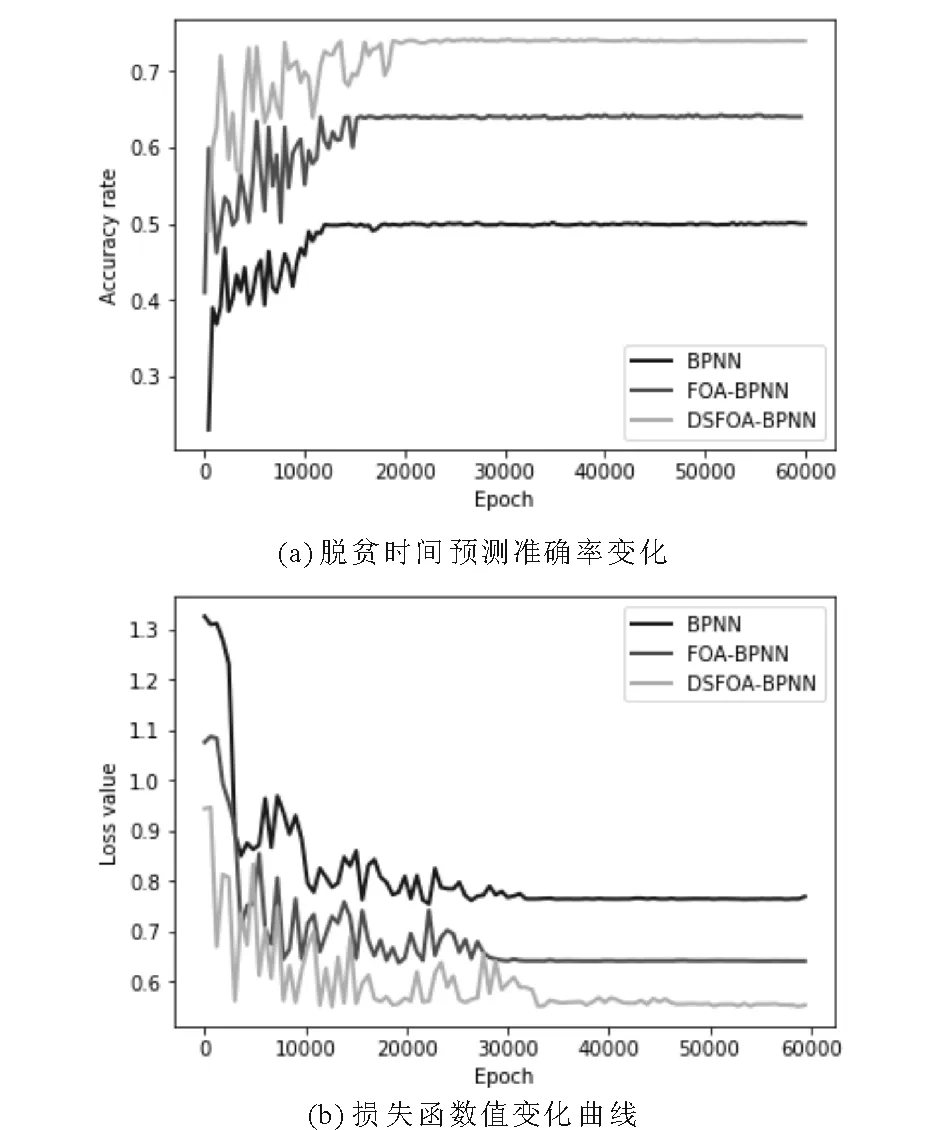
圖4 訓練樣本為50000時模型預測準確率與損失函數值變化曲線Fig.4 The curves of the accuracy rate and loss value with 50000 samples

從圖4(a)中我們可以看出，BPNN模型在隨機初始參數下脫貧時間預測的準確率在22%左右，對于一個三分類問題，所選的初始參數顯然無法達到預期效果；模型預測準確率最終穩定在50%，準確率不夠高.針對建模方法及過程，結合現有條件，分析造成上述現象的原因之一可能在于隨機選擇的初始參數不合適，模型在訓練后期無法掙脫局部解空間，因此需要借助尋優算法提高模型初始參數的質量，提升模型的收斂精度.

針對上述問題，根據提出的果蠅優化算法優化BP神經網絡的方案，利用標準FOA與DSFOA優化BP神經網絡，進一步進行實驗驗證，實驗結果如圖4(a)中FOA-BPNN與DSFOA-BPNN所示.測試集對應的3種方法預測準確率的對比如表1所示.

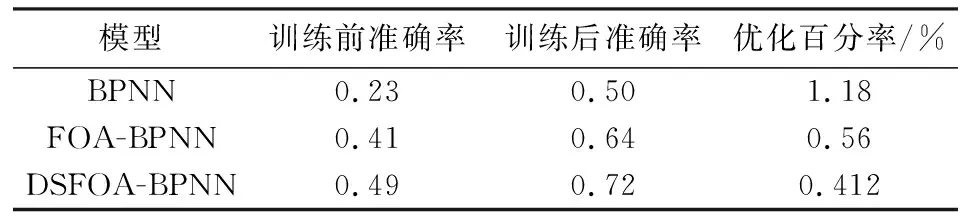
表1 模型訓練前后準確率對比Tab.1 Accuracy rate comparison before and after model training

FOA-BPNN預測模型的初始參數是經過果蠅優化算法優化后得到的，由圖4(a)可以看出模型在初始參數下的預測準確率為50%左右，遠高于BPNN的22%，FOA-BPNN脫貧時間預測準確率最終穩定在65%左右，相較于BPNN有了一定提高.產生上述結果的根本原因在于初始參數選擇，初始參數不僅決定了模型的初始準確率，在一定程度上也影響了模型跳出局部最優的能力，進而影響模型最終的預測準確率.這表明相較于利用正態分布隨機取得初始參數的模型，由果蠅優化算法選擇初始權重和閾值的模型在訓練過程中更容易得到最優的權重和閾值.

通過對果蠅優化算法的步長變化進行調整，形成DSFOA-BPNN預測模型，在初始參數下模型預測準確率為50%，模型的最終預測準確率穩定在73%左右，在一定程度上提升了脫貧時間預測的準確率.上述結果表明動態果蠅優化算法(DSFOA)對初始參數的優化效果要好于標準果蠅優化算法.這是因為標準果蠅優化算法在尋優過程中搜索步長固定，容易陷入局部最優的困境；而動態步長果蠅優化算法在尋優的不同階段根據需要賦予果蠅個體不同的搜索步長，獲得最優初始參數的幾率更大.

圖4(b)為3種方法建模過程中損失函數的變化趨勢.實驗過程中的平均損失是交叉熵損失與正則化損失之和，如式(7)所示：

loss=cross_entropy_mean+regularaztion,

(7)

其中loss為總損失，cross_entropy_mean表示平均交叉熵損失，regularaztion指正則化損失，交叉熵作為評判輸出向量和期望向量接近程度的方法之一，刻畫了兩個概率分布之間的距離.正則化項為L2型正則化，在一定程度上解決了過擬合問題，提高了泛化能力.

3種方法在建立預測模型的過程中損失函數變化曲線都呈下降趨勢.由圖4(b)可知BPNN與FOA-BPNN、DSFOA-BPNN的初始損失值不同，前者的初始參數明顯要劣于后者，產生的誤差損失較高.BPNN模型隨著訓練次數增加，模型損失逐漸下降，最終穩定在0.78左右.FOA-BPNN的初始參數下模型損失約為1.1，經過若干輪訓練，誤差函數值穩定在0.64左右，相較于BPNN減少了22%；進一步優化果蠅優化算法的步長選擇，最終DSFOA-BPNN的誤差函數值穩定在0.57.

為了進一步驗證3種方法的性能，在原有數據集上新增一個縣的扶貧數據45000條，按照4∶1的比例對數據集進行分割，形成訓練集與測試集，分析3種方法在發生數據增量時的性能.當訓練樣本增加近一倍時，對比圖4和圖5，3種模型訓練前期準確率震幅增大，收斂時間增加.結合表2與圖5(a)，BPNN與FOA-BPNN的穩定性與收斂精度影響不大；對于DSFOA-BPNN，數據量的增大并未對模型的預測精度造成較大負面影響，然而由于噪聲數據隨著數據量的增加而增加，模型在訓練前期的震蕩加重，從圖5(b)可以看出DSFOA-BPNN在訓練Epoch值達到15000時，損失函數值出現一次較明顯的波動，這是因為總損失由正則化損失和交叉熵損失組成，噪聲加劇導致正則化損失增加.

圖5 訓練樣本為95000時模型預測準確率與損失函數值變化曲線Fig.5 The curves of the accuracy rate and loss value with 95000 samples

Tab.2 Accuracy comparison of incremental experimental models before and after training

模型訓練前準確率訓練后準確率優化百分率/%BPNN0.2270.4981.19FOA-BPNN0.400.6380.575DSFOA-BPNN0.500.710.40

3 總結與展望

本文提出了一種DSFOA-BPNN模型對脫貧時間預測進行準確刻畫與定量分析，在對某地區貧困戶基本信息進行預處理后，建立特征量映射數據庫，將改進的果蠅優化算法與BP神經網絡結合，實現對脫貧時間的有效預測.實驗對比表明：在對貧困戶脫貧時間預測的應用中，DSFOA-BPNN預測模型具有較好的預測效果.下一步將更全面地考慮貧困戶的各項屬性及其相互之間的關聯，提高模型的準確率與實用性.