Archimedean Copula函數在風電場功率爬坡風險評估領域中的應用

程亞麗， 王致杰， 江秀臣

(1. 上海電機學院 電氣學院，上海 201306； 2. 上海交通大學 電氣工程學院，上海 200240)

目前，對功率爬坡事件的研究主要集中于爬坡預測上[1]，而爬坡事件對電網產生的風險的研究很少，且只是對爬坡單一特征量進行分析[2]，已經很難滿足對于極端氣候變化特征和電網風險管理的需求。因此，有必要對爬坡要素間的相互關系和聯合概率分布特征進行研究。Sklar[3]在1959年提出的Archimedean Copula函數，是一類將變量聯合分布函數與邊緣分布函數連接在一起的函數，很好地描述變量之間的相關性并計算其聯合概率分布。聯合分布里包含了所有風險要素的信息，可以全面評估事件的風險大小，被廣泛地用于水文事件、干旱、沙塵暴等方面的多變量研究中[4-10]。文獻[11-13]把Copula理論運用到了金融市場的風險分析中，分析風險因子之間的相關性；文獻[14-16]結合Copula理論對投資組合風險進行度量，能夠更準確地度量投資組合的風險值。但是將此函數運用在風電場功率爬坡風險評估方面較少，本文利用Archimedean Copula函數多維聯合的靈活性，構建風電功率爬坡事件的二維聯合分布，建立了萊州風電場發生功率爬坡的概率模型，定量分析風電場發生功率爬坡的風險，為風電場功率爬坡風險評估研究提供新的思路。

1 風電場功率爬坡特征量的選取

在短時間內風電功率的劇烈波動使得風力發電具有不確定性、間斷性和隨機性，這種現象被稱為風電功率爬坡事件，描述一個爬坡事件的主要特征量是確定的，包括爬坡幅值、爬坡方向、爬坡率、爬坡起止時間和持續時間，如圖1所示。爬坡幅值通常是在爬坡持續時間內最大和最小功率的差值，爬坡方向用爬坡幅值的正負表示，正代表上爬坡事件，負代表下爬坡事件。

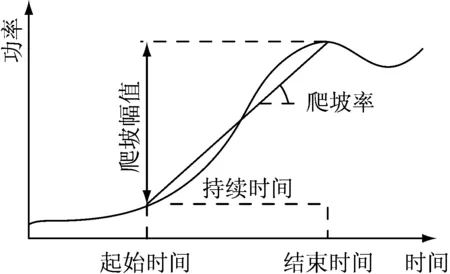
圖1 爬坡事件特征圖

由圖1可見，爬坡幅值越大，爬坡持續時間越短，則爬坡事件越嚴重。因此，選取爬坡幅值和爬坡持續時間這兩個特征量作為風電功率爬坡事件的主要特征量，建立二維聯合分布。

2 Archimedean Copula函數

Archimedean Copula函數主要包括Frank Copula、Clayton Copula和Gumbel Copula函數，本文選用3種二維Archimedean Copula函數進行爬坡特征量二維聯合，具體的分布函數及參數范圍如表1所示。

對于Archimedean Copula函數擬合度的檢驗方法通常采用離差平方和(Oridinary Least Square,OLS)準則法，采用文獻[5]中的OLS準則法公式。該函數參數擬合度優劣的判斷依據是OLS越小，表明該Archimedean Copula與其經驗點距的誤差越小，函數擬合程度越好。

表1 二維Archimedean Copula分布函數及參數范圍

表1中，u1，u2為Archimedean Copula函數中的兩個隨機變量。

3 基于Archimedean Copula函數的爬坡特征量聯合分布

3.1 爬坡特征量邊緣分布函數

通過對目前國內外概率分布函數的研究，本文假定爬坡持續時間服從對數正態分布，風電功率爬坡幅值服從廣義極值分布，則相應的分布函數和概率密度函數設計如下：

設隨機變量x的樣本點為x1,x2,…,xn，隨機變量指的是風電功率爬坡持續時間的實際數據，對數正態分布的概率密度函數為

(1)

風電功率爬坡持續時間t的累積分布函數為

(2)

式中：μ為隨機變量的均值，也稱為位置參數；σ2為標準差，也稱為形狀參數。

極值分布是指在概率論中極大值(或者極小值)的概率分布，概率密度函數為

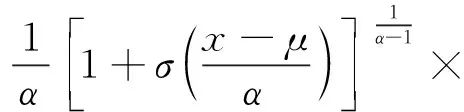
(3)

爬坡幅值ΔP的累積分布函數為

(4)

式中，α為尺度參數。

利用極大似然函數進行邊緣分布參數估計，爬坡持續時間的參數估計計算公式如下：

(5)

對式(5)兩邊取對數，得

(6)

根據式(6)建立似然函數組為

(7)

可得

式中：L(μ，σ2)為似然函數；ti為爬坡持續時間變量。爬坡幅值分布函數的參數估計按照式(5)～式(7)類推。

4 實例研究

本章算例采用的數據是2015年一年萊州風電場的實測數據，風力發電機組的輸出功率每15 min采樣一次，分別采用對數正態分布、廣義極值分布對爬坡持續時間和爬坡幅值進行擬合，利用極大似然法對各邊緣分布函數進行參數估計，并通過K-S法對各邊緣分布函數進行檢驗。采用Archimedean Copula函數構建風電功率爬坡幅值和爬坡持續時間的聯合概率分布模型，并根據OLS準則法最小原則，選取最合適的Archimedean Copula函數構建爬坡幅值和爬坡持續時間的聯合概率分布函數。

4.1 爬坡特征量擬合分布

運用極大似然法分別對爬坡持續時間、幅值的邊緣分布函數參數進行估計，結果如表2所示。利用K-S法對各分布函數進行檢驗，取K-S檢驗的顯著性水平α=0.05，當n=44時，查詢檢驗分位數表得到對應的分位點D0=0.200 56，當邊緣分布的檢驗統計量D<0.200 56時，表明K-S檢驗通過且擬合情況較好。爬坡幅值、持續時間的K-S檢驗的計算結果如表3所示，對數正態分布和廣義極值分布對于爬坡特征量的擬合檢驗值都通過了0.05的顯著性檢驗，說明上述兩種概率分布函數對于爬坡特征量的擬合效果較好。因此，選取廣義極值分布進行爬坡幅值邊緣分布的擬合，選取對數正態分布進行爬坡持續時間邊緣分布的擬合。

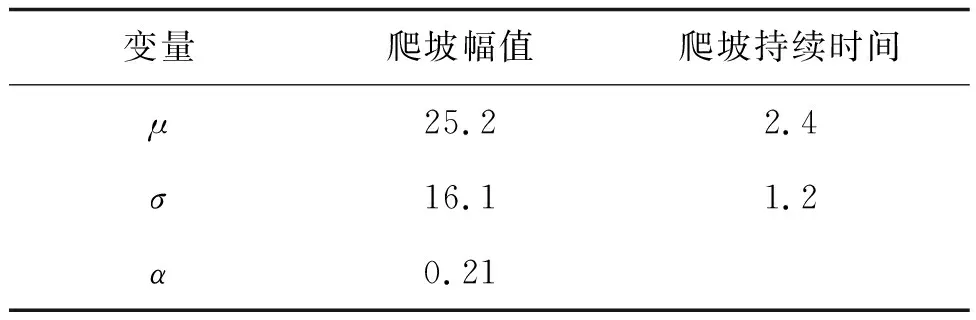
表2 邊緣分布函數的參數值

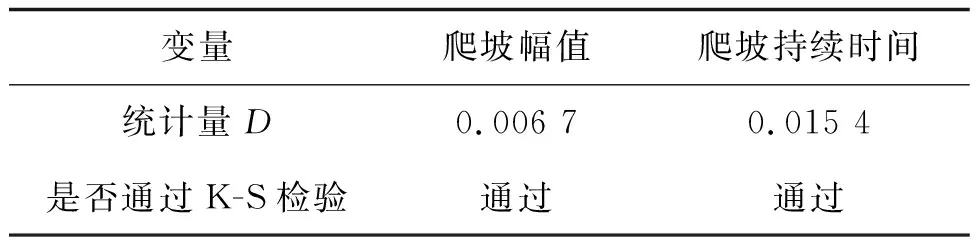
表3 爬坡特征變量的K-S檢驗

4.2 爬坡特征量二維聯合分布

對爬坡特征量中的爬坡持續時間和爬坡幅值構建Archimedean Copula函數二維聯合分布，利用式(5) ～式(7) 進行參數估計，采用表1中的函數公式進行二維擬合，通過OLS準則法進行優度檢驗，相關參數及檢驗值見表4。

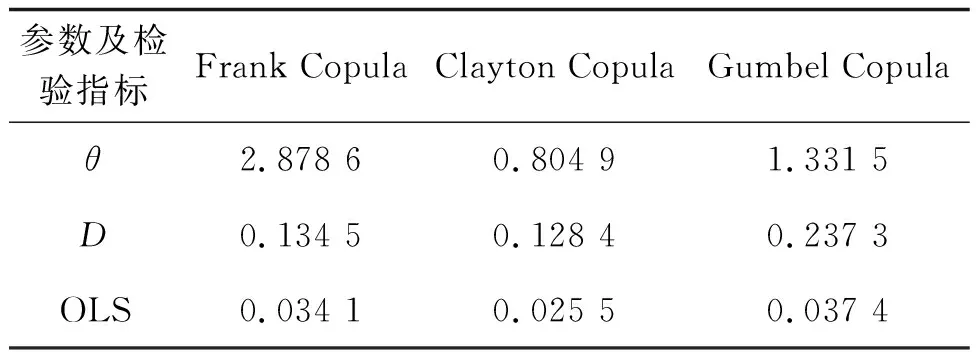
表4 分布函數參數及檢驗值

從表4中可見，從K-S檢驗統計量D值分析，3種Archimedean Copula聯合函數的D值都小于臨界值0.200 56。因此，3種函數都可以構建萊州風電場爬坡持續時間與爬坡幅值的聯合分布模型；從擬合優度的評價指標分析，Clayton Copula函數構建的聯合分布模型的OLS值最小，擬合效果最優。因此，選取Clayton Copula函數模型為萊州風電場爬坡持續時間與爬坡幅值的聯合分布模型。

為了進一步驗證擬合效果的優劣，利用Matlab軟件對萊州風電場爬坡持續時間與爬坡幅值的數據編程，Frank Copula函數可以很好地描述對稱的相關關系，以Frank Copula函數為例，運用Matlab求Frank Copula函數參數程序如下。

?

調用copulafit函數估計二元Frank Copula中的參數

rho_norm = copulafit('Frank',[U(:), V(:)])

[Udata,Vdata] = meshgrid(linspace(0,1,31));

Cpdf_norm = copulapdf('Frank',[Udata(:), Vdata(:)],rho_norm);

Ccdf_t = copulacdf('t',[Udata(:), Vdata(:)],rho_t,nuhat);

繪制二元Frank Copula的密度函數圖

figure;

surf(Udata,Vdata,reshape(Cpdf_norm,size(Udata)));

xlabel('爬坡持續時間');

ylabel('爬坡幅值');

zlabel('二元Frank Copula密度函數)');

?

通過Matlab仿真，得到爬坡持續時間與爬坡幅值的概率密度分布圖如圖2～4所示。Frank Copula函數具有對稱性，尾部很厚，可用于描述具有對稱的相關關系(見圖2)。由于風電場發生嚴重爬坡事件和一般爬坡事件時不具有對稱性，因此該函數不能很好地描述風電場功率爬坡嚴重事件引起的風險。Gumbel Copula函數分布似“J”形，擁有較厚的上尾部特征，上尾部特征是描述變量間同時出現大的變化的概率(見圖3)。風電功率爬坡特征量的Gumbel Copula函數上尾部特征突出，不能很好地描述風電場中爬坡幅值較大且爬坡持續時間較短的極端爬坡事件。Clayton Copula不具有對稱性，分布似“L”形，具有較厚的下尾部特征(見圖4)。風電功率爬坡特征量的Clayton Copula函數具有很好的下尾部特征，能較好地描述極端爬坡事件小概率發生的現象，從而可以分析極端事件引起的損失。

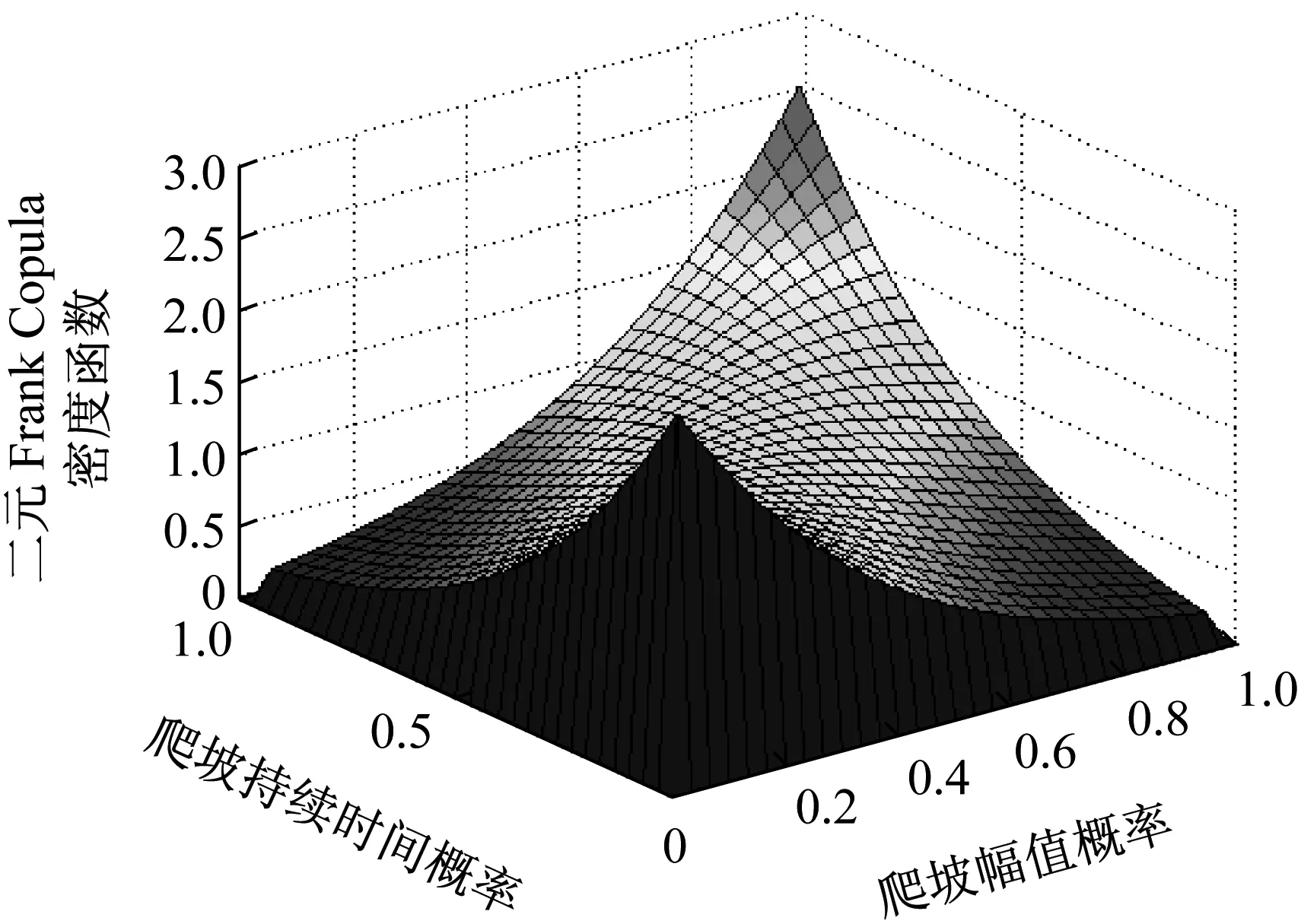
圖2 Frank Copula函數的爬坡幅值和爬坡持續時間概率密度分布

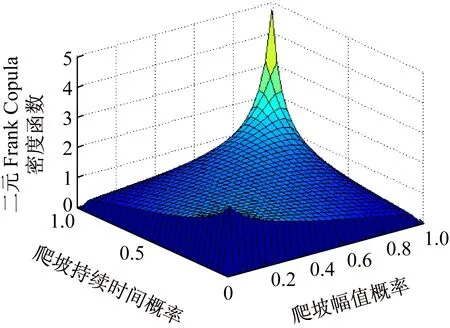
圖3 Gumbel Copula函數的爬坡幅值和爬坡持續時間累計概率分布

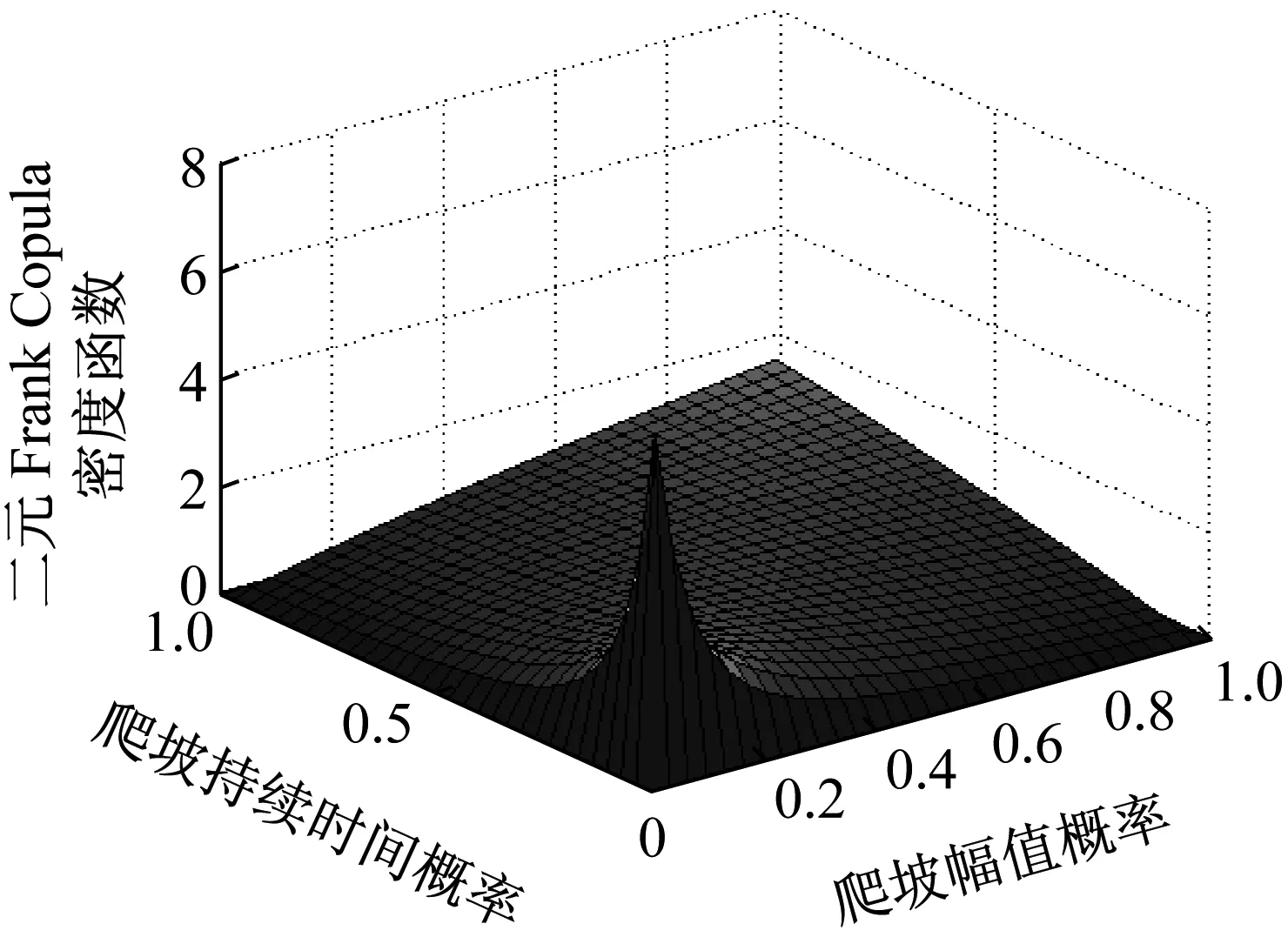
圖4 Clayton Copula函數的爬坡幅值和爬坡持續時間概率密度分布

根據上述分析可知，可用Clayton Copula函數描述萊州風電場功率爬坡幅值和爬坡持續時間的聯合分布，表達式如下：

FΔP,t=Cu1,u2=

(8)

萊州風電場功率爬坡幅值和爬坡持續時間的聯合分布概率計算模型如下：

F(ΔP1? ΔP? ΔP2,t1?t?t2)=

F(ΔP2t2)-F(ΔP2,t1)-F(ΔP1,t2)+

F(ΔP1,t1)

(9)

該模型同時包含了爬坡幅值和爬坡持續時間信息，可準確地計算爬坡事件發生的概率，能定量分析風電功率爬坡事件的風險評估，方便調度人員更好地做出調度策略，減少風險引起的損失。

5 結 語

選取了風電功率爬坡事件的爬坡持續時間和爬坡幅值兩個特征量，對其采用對數正態分布和廣義極值分布進行邊緣分布擬合，并在建立風電功率爬坡幅值和爬坡持續時間邊緣分布模型中，推導了利用極大似然法進行參數估計的過程，最后采用K-S檢驗法對擬合優度檢驗。在此基礎上，根據3種Archimedean Copula函數模型的表達式建立了爬坡幅值和爬坡持續時間的二維聯合分布函數，并采用OLS準則法作為擬合優度的評價指標，確定了Clayton Copula模型作為萊州風電場爬坡事件概率計算模型，從而定量地分析風電場功率爬坡的風險。本文為風電場功率爬坡風險評估方面提供一定的理論依據和支撐，拓展了Copula理論的應用前景。