四節點手性拉脹超材料在彈塑性大變形下的等效力學性能研究
朱一林, 朱一立
(1.成都大學 建筑與土木工程學院, 四川 成都 610106;2.煙臺大學 機電汽車工程學院, 山東 煙臺 264005;3.冰輪環境技術股份有限公司, 山東 煙臺 264000)
0 引 言
拉脹超材料是自20世紀90年代起迅速發展起來的一類功能和結構一體化的多孔材料[1-3].與常規材料相反,當拉脹超材料承受單軸拉伸(壓縮)載荷時,在與負載垂直的方向上出現膨脹(收縮)而表現出負泊松比效應.由于這種特殊的變形形式,拉脹超材料相較于傳統多孔材料具有更優越的性能,如超常彈性常數、抗壓痕性、抗沖擊性、抗斷裂韌性、可變滲透性以及聲學和能量吸收性能等[3-4].此外,拉脹超材料還表現出同向曲率的獨特物理性能[5].這些獨特的力學和物理特性使拉脹超材料在航空航天、生物醫學和傳感器等[6-9]領域有廣泛的應用前景.
手性拉脹超材料是目前被廣泛研究的一類典型二維拉脹超材料,其元胞結構由一個中心圓環與幾條與圓環相切的手臂組成.根據手臂數目的不同,手性拉脹超材料可相應地分為三節點、四節點和六節點結構.由于等效力學性能,如泊松比和彈性模量,是設計拉脹超材料的重要指標并且也是建立相應本構模型的基礎,科研人員通過實驗以及數值方法對其進行了系統的研究[10-12].需要指出的是,上述研究大都局限在小變形彈性框架下,而拉脹超材料在使用過程中通常會發生彈塑性大變形.對此,本研究針對四節點手性元胞結構的拉脹超材料在彈塑性大變形下的等效力學性能,包括泊松比、彈性模量和塑性強化應力,進行分析,擬對手性拉脹超材料的改良設計以及相應本構模型的建立提供依據.
1 分析方法
1.1 元胞尺寸
根據Alderson等[10]的方法,四節點手性拉脹超材料的元胞結構(見圖1)可由3個面內幾何參數來描述,即圓環長度r、手臂長度l以及厚度t.需要指出的是,本研究假設四節點手性拉脹超材料的面外尺寸遠大于面內尺寸,因此,在其數值計算中可采用平面應變假設.圖1中元胞結構的相對尺寸為l∶r∶t=22∶5∶1.25,其相對密度約為18%.

圖1四節點手性拉脹超材料元胞結構
1.2 基體材料屬性
本研究采用AA6061-T4鋁合金為所分析拉脹結構的基體材料,其材料性能參考文獻[13].基體材料的彈性模量和泊松比分別為110 GPa和0.28,其塑性硬化行為由表1確定.數值計算采用ABAQUS分析軟件完成.計算中所用的單元類型為CPE4二維大變形平面應變單元.基體材料本構模型為簡單彈性—多線性塑性本構模型.

表1 AA6061-T4鋁合金的應力—塑性應變特性
1.3 基于周期性邊界條件的均勻化方法
本研究的四節點手性拉脹超材料的等效力學性能由基于ABAQUS分析軟件的數值均勻化方法來確定.為了消除邊界條件的影響,計算時對元胞結構施加如式(1)所示的周期性邊界條件[14],
(1)
式中,x+和X±分別為元胞相對平面的空間和參考坐標;t±=P±N±代表外法向為N±平面上節點的牽拉應力,其中,P為第一類皮奧拉—基爾霍夫應力.
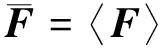
(2)
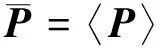
(3)
式(2)、(3)中,V0、?V0分別為元胞在參考坐標系下的體積和邊界.
元胞的整體變形可由Biot應變[15]來度量,即,
(4)
式中,l為二階單位張量.
參照Ciambella等[16]的研究,等效泊松比定義為,
(5)
分析時,彈性模量可通過加、卸載的應力—應變曲線來測定.
2 等效力學性能
本研究通過數值計算方法分析了四節點手性拉脹超材料的等效泊松比、等效彈性模量以及等效塑性強化應力.為了獲得不同取向的性能,在數值計算時,元胞的取向(以圖1中的角度θ表征)從0 °旋轉到360 °.
2.1 等效塑性強化應力
四節點手性拉脹超材料在不同取向時的等效應力—應變曲線如圖2所示.
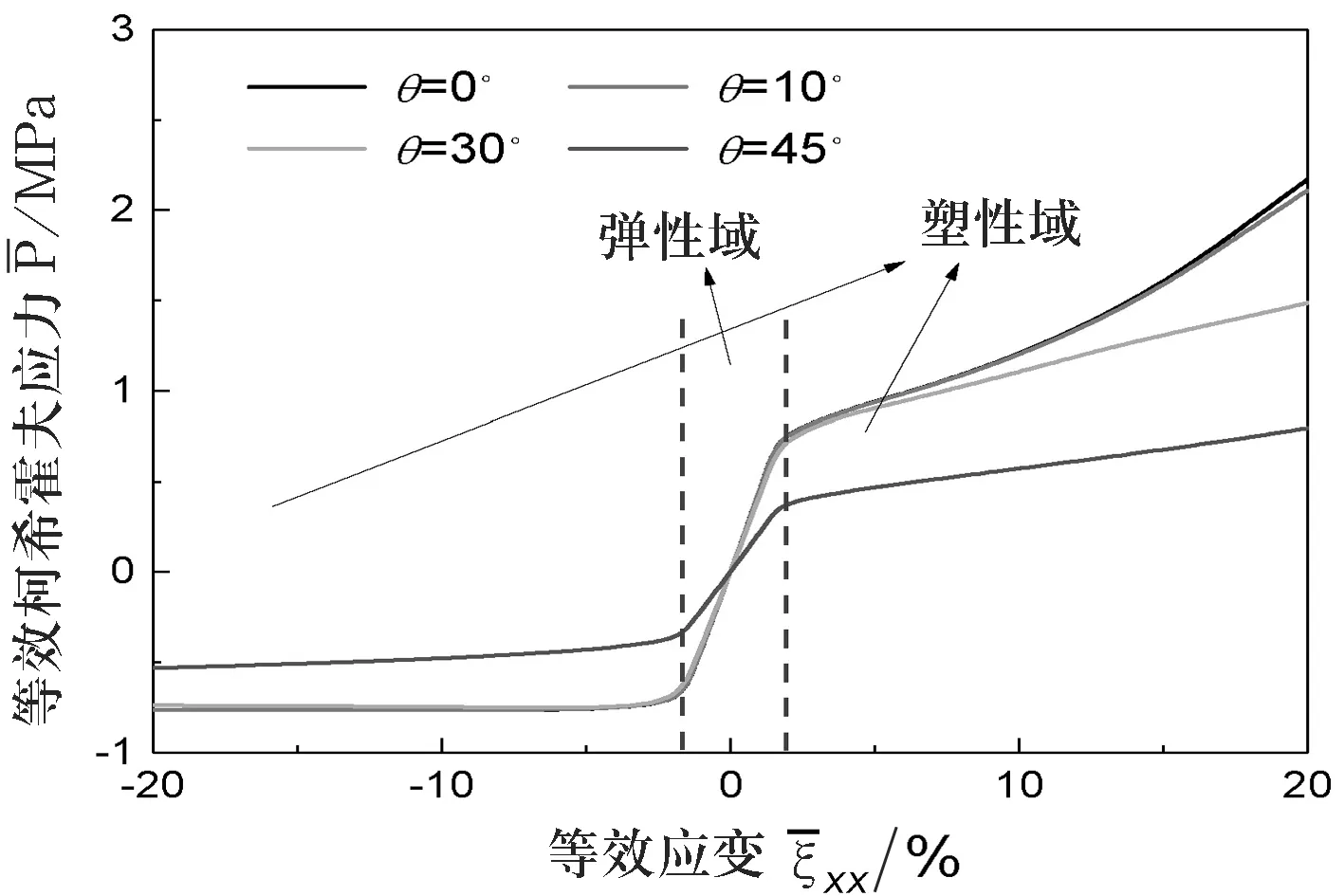
圖2不同元胞取向時的等效應力—應變關系
由圖2可見,同傳統金屬材料一樣,該拉脹超材料的等效應力—應變曲線也可分為彈性和塑性兩部分,且拉伸和壓縮時呈現不同的強化模式.拉伸塑性屈服時呈指數硬化的特征,壓縮塑性屈服時呈理想塑性硬化的特征.此外,圖2還表明,不同取向時該拉脹超材料表現出不同的等效應力—應變關系.
為了更好地觀察該拉脹超材料在整個面內的屈服強化行為,本研究進一步給出了其在不同變形時的等效強化應力—取向角度極坐標圖(見圖3).
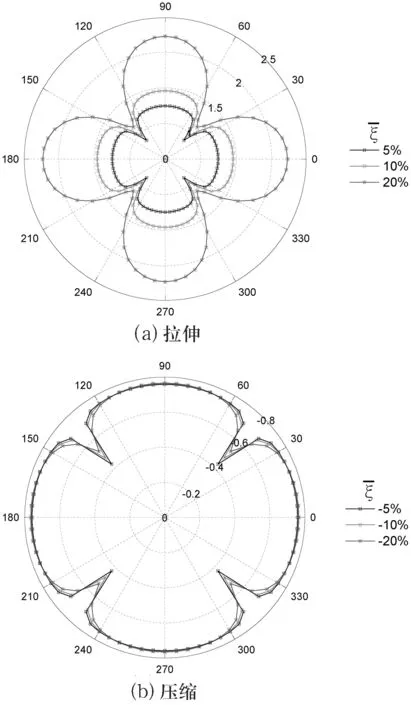
圖3不同變形時的等效強化應力—角度關系(極坐標圖)
由圖3可見,該拉脹超材料的等效強化應力不具備各向同性,而是呈現出4度旋轉對稱(旋轉角為90 °)的特征.當角度θ=(k/2)π(k=0,1,2,3,4)時,材料的強度最大;當角度θ=(1/4+k/2)π(k=0,1,2,3)時,材料的強度最小.
2.2 彈性模量
四節點手性拉脹超材料在不同取向時的等效彈性模量隨應變的演化曲線如圖4所示.
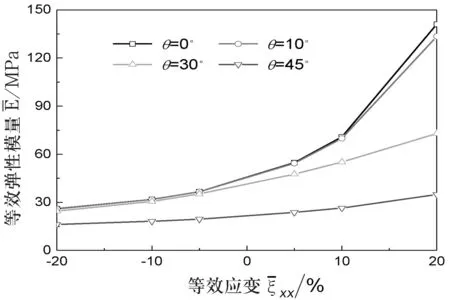
圖4不同元胞取向時的等效彈性模量演化
由圖4可見,本拉脹超材料在不同取向時的等效彈性模量均隨應變的增加呈指數演化趨勢,且不同的取向具有不同的演化速度.
同樣,為了更好地觀察該拉脹超材料在整個面內的等效彈性模量演化行為,本研究進一步給出了其在不同變形情況下的等效彈性模量—取向角度極坐標圖(見圖5).
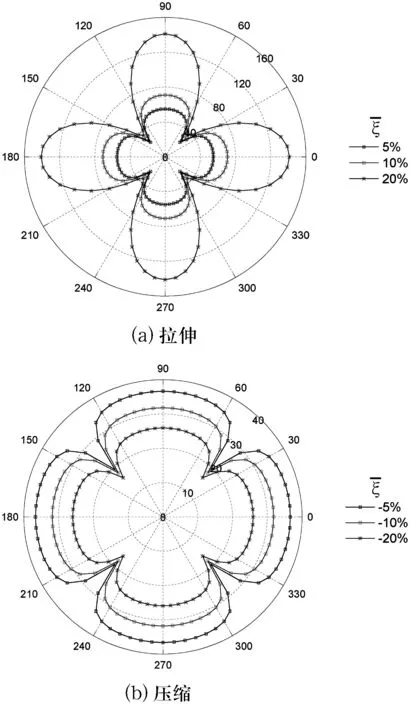
圖5不同變形時的等效彈性模量—角度關系(極坐標圖)
由圖5可見,該拉脹超材料的等效彈性模量也呈現出4度旋轉對稱(旋轉角為90 °)的特征.同樣,當角度θ=(k/2)π(k=0,1,2,3,4)時,材料的剛度最大;當角度θ=(1/4+k/2)π(k=0,1,2,3)時,材料的剛度最小.
2.3 泊松比
四節點手性拉脹超材料在不同取向角度下的等效泊松比演化曲線如圖6所示,在不同變形情況下的等效泊松比—取向角度極坐標圖如圖7所示.
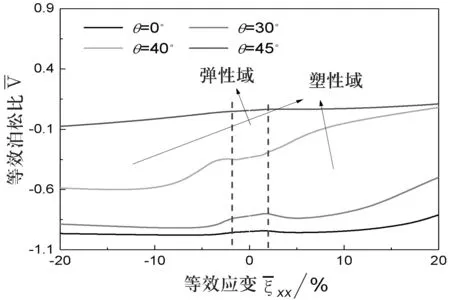
圖6不同元胞取向時的等效泊松比演化
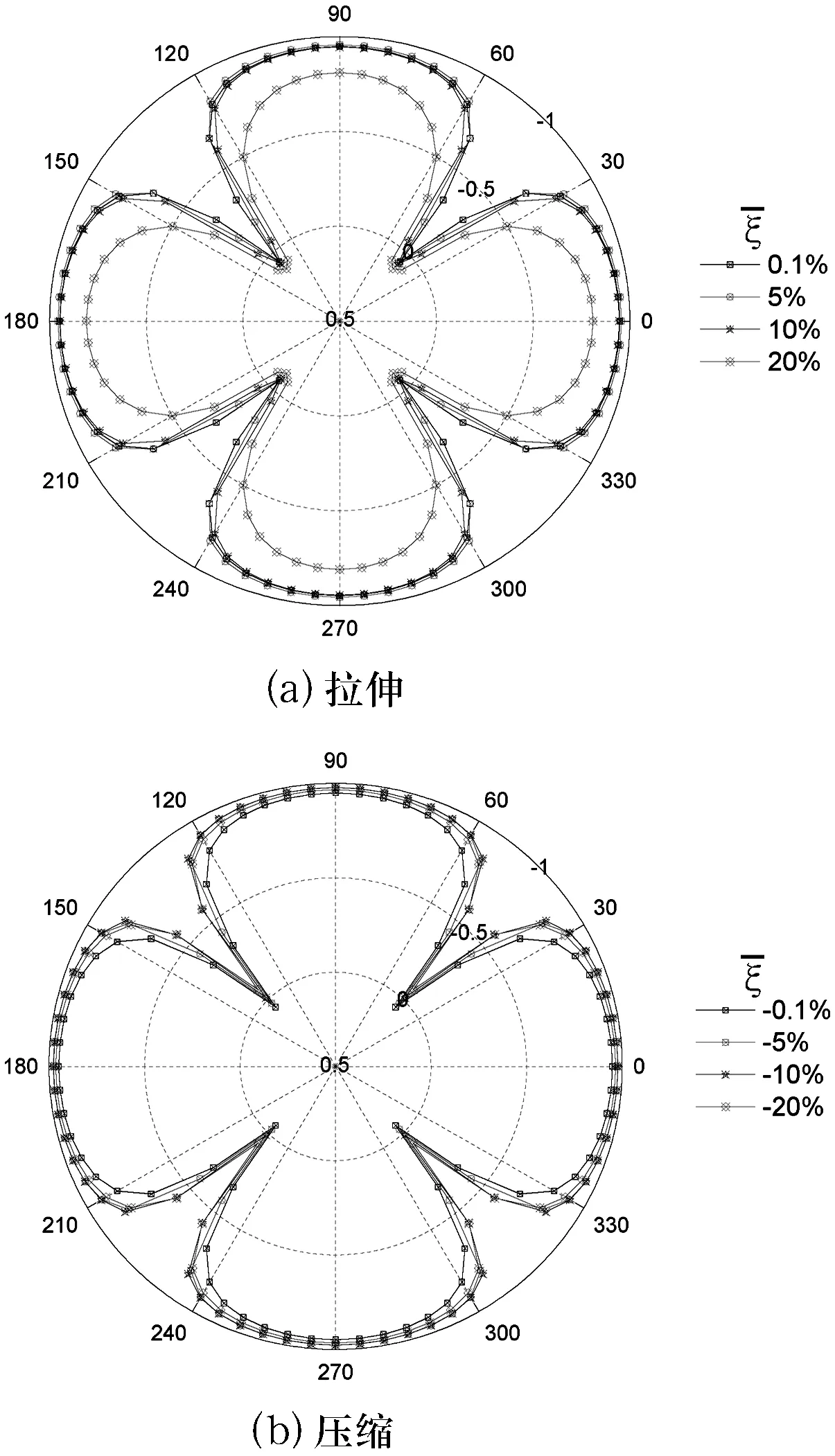
圖7不同變形時的等效泊松比—角度關系(極坐標圖)
由圖6、7可見,在大變形時,該拉脹超材料的等效泊松比不再為恒定值,而是隨著變形的演化而演化,且在不同的取向角度表現出不同的負泊松比效應,其等效泊松比的極坐標圖同樣呈現出4度旋轉對稱(旋轉角為90°)的特征.即,在角度θ=(k/2)π(k=0,1,2,3,4)時,材料的負泊松比效應最大;當角度θ=(1/4+k/2)π(k=0,1,2,3)時,材料的負泊松比效應最小.
3 結 論
本研究采用周期性邊界條件的數值均勻化方法,系統地分析了四節點手性拉脹超材料在彈塑性大變形下的等效力學性能,得到了如下結果:
1)在彈塑性大變形時,材料的等效力學性能不再是恒定值,而是隨著變形的變化而演化.
2)等效強化應力、等效彈性模量和等效泊松比的面內極坐標圖均呈現出4度旋轉對稱(旋轉角為90°)的特征.
3)當角度θ=(k/2)π(k=0,1,3,4)時,材料的強度、剛度以負泊松比效應最大;而當角度θ=(1/4+k/2)π(k=0,1,2,3)時,材料的強度、剛度以及負泊松比效應最小.

