考慮躍遷系數的軸向受力鐵木辛科梁的自由振動
陳岳陽, 李翔宇
(西南交通大學 力學與工程學院, 四川 成都 610031)
0 引 言
目前,承受軸向力作用的梁廣泛應用于土木工程,生物醫學和機械制造等領域[1-3].由于軸向受力的梁具有優良的拉伸和彎曲性能,其力學行為,例如振動,屈服,彎曲等,一直受到科研人員的廣泛關注[4-7].值得指出的是,在軸向受力鐵木辛科梁的變形過程中,軸向力的作用方向在相關文獻中有兩種假設:第一種是假定軸向力與梁的中性軸相切[8-9];另一種則認為軸向力垂直于變形后的梁的橫截面[10-11].這兩種假設導致軸向受力的鐵木辛科梁的力學行為呈現不同的結果,即軸向受力鐵木辛科梁的許多力學問題仍需要做進一步探討.基于此,本研究著重分析了軸向受力鐵木辛科梁的自由振動問題,同時系統地探究了軸向力的作用方向對該梁的影響.
1 統一模型和特征方程
1.1 統一模型
在笛卡爾坐標系Oxy下,考慮長度為L,高度為h的鐵木辛科梁,其中包含著軸向力F(假設其在變形過程中保持不變)和一個外加的橫向均布簡諧載荷p(x,t),具體如圖1所示.
軸向載荷的作用方向對梁的力學行為非常重要,在文獻中對此存在兩種假設.這兩種假設在歐拉梁模型中是一樣的,但是對于鐵木辛科梁來說,這兩種假設會導致不一樣的結果.對此,2016年,陳濤等[12]
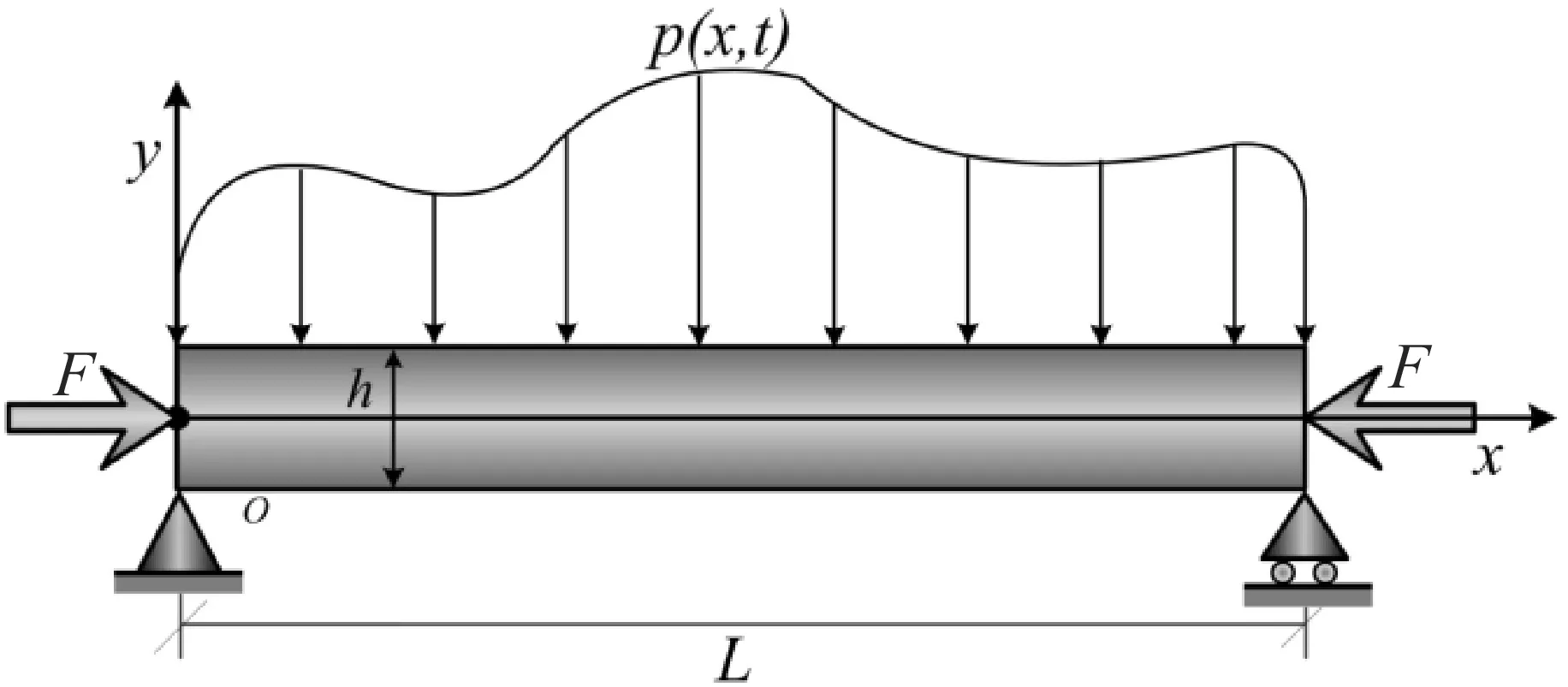
圖1鐵木辛科梁模型示意圖
建立了一個統一的模型并引入一個躍遷系數(α)來表示軸向力的作用方向,α的取值范圍為0到1,而上述兩種假設能夠由躍遷系數取特定值,即0或1,來實現.
在統一模型中,彎矩M和豎直方向的剪力V可表示為,
M=EIΨ′
(1)
V=κGA(Ψ-w′)+F[w′+α(Ψ-w′)]
(2)
根據牛頓第二定律,可得到如下的控制方程,
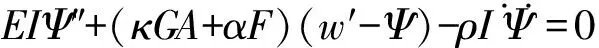
(3)
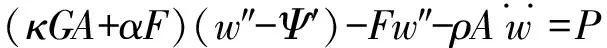
(4)
式中,κ,I,ψ,w,E,G,F,A和α分別代表著剪切修正因子、慣性矩、扭轉角、撓度、剪切模量、楊氏模量、軸向力、截面面積和躍遷系數,式中的“·”和“′”分別
表示對時間t和空間坐標x的導數.
在研究中,假定一個壓縮(或拉伸)軸向力為正(或負),通過改變相應的系數,式(3)和式(4)可以退化成歐拉梁或瑞利梁的相應運動方程.
消去式(3)及(4)中的轉角ψ,鐵木辛科梁控制方程可以轉化為位移表示的偏微分方程,
(5)
式中,
c1=κGA+αF-F,c2=κGA+αF.
在本研究中,只分析鐵木辛科梁的自由振動,故假設,
w(x,t)=W(x)eiΩt
(6)
式中,W表示橫向振動的振幅,Ω表示為系統的圓頻率.
將式(6)帶入式(5)中可得,
W″″+λ1W″+λ2W=0
(7)
式中,λ1=a1+a2Ω2,λ2=a4Ω4-a3Ω2.
事實上,歐拉梁和瑞利梁的自由振動微分方程和鐵木辛科梁的方程(7)相同,僅除了歐拉梁和瑞利梁的微分方程中參數的表示不同.表1中給出了其對應參數的表達式.
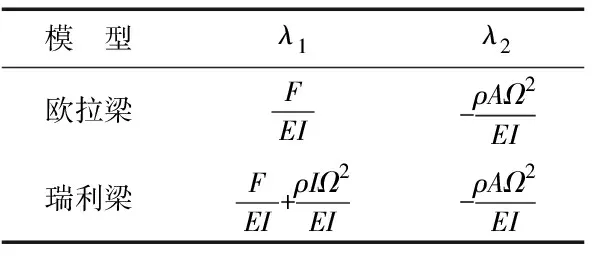
表1 歐拉梁和瑞利梁的參數形式
對應于歐拉梁和瑞利梁,躍遷系數α不包含λi(i=1,2)的表達式,這是因為歐拉梁和瑞利梁的橫截面在變形過程中的正方向假定為與撓曲線切線平行.
1.2 頻率方程
從文獻[4]可知,式(7)依賴于截止頻率,
式(7)的通解可以表達成以下形式,
W(x)=A1coshs1x+A2sinhs1x+A3coss2x+
A4sins2x,Ω<Ωc
(8)
式中,
為方程的特征根.此外,Ai(i=1,2,3,4)為待定常數.
在文獻[4]中詳細闡述了截止頻率的物理意義,本研究的分析將限制在Ω<Ωc的情況下.
為了確定固有頻率,需要確定鐵木辛科梁的邊界條件.由于躍遷系數的引入,邊界條件與相關文獻相比將呈現不同的形式,其中系數α設置為1或0.表2為邊界條件.

表2 邊界條件
其中,
由通解和表2的邊界條件,易得鐵木辛科梁的頻率方程如表3所示.

表3 頻率方程
其中,
2 數值分析
2.1 有效性驗證
考慮一個正方形截面(b=h=0.1 m)的鐵木辛科梁,其長度L=0.5 m,密度ρ=2 778 kg/m3,楊氏模量E=7×1010N/m2,剪切模量G=2.61×1010N/m2.本研究利用此梁建立有限元模型來驗證本研究方法的準確性,同時考慮采用多種邊界條件來驗證本研究的解析結果.為此,采用了正方形截面的簡支梁、簡支—滑動梁和固支梁,使用有限元軟件ANSYS進行數值模擬,其中單元為beam 189,并將梁劃分為201個節點.
引入Ncr和Ω0作為無量綱化的參考量.其中,Ncr表示不同邊界條件的臨界屈曲載荷.Ω0是無軸力時正方形截面(b=h=0.1 m)的簡支鐵木辛科梁的基頻[9].
1)無軸力時,無量綱頻率的對比情況如圖2所示.
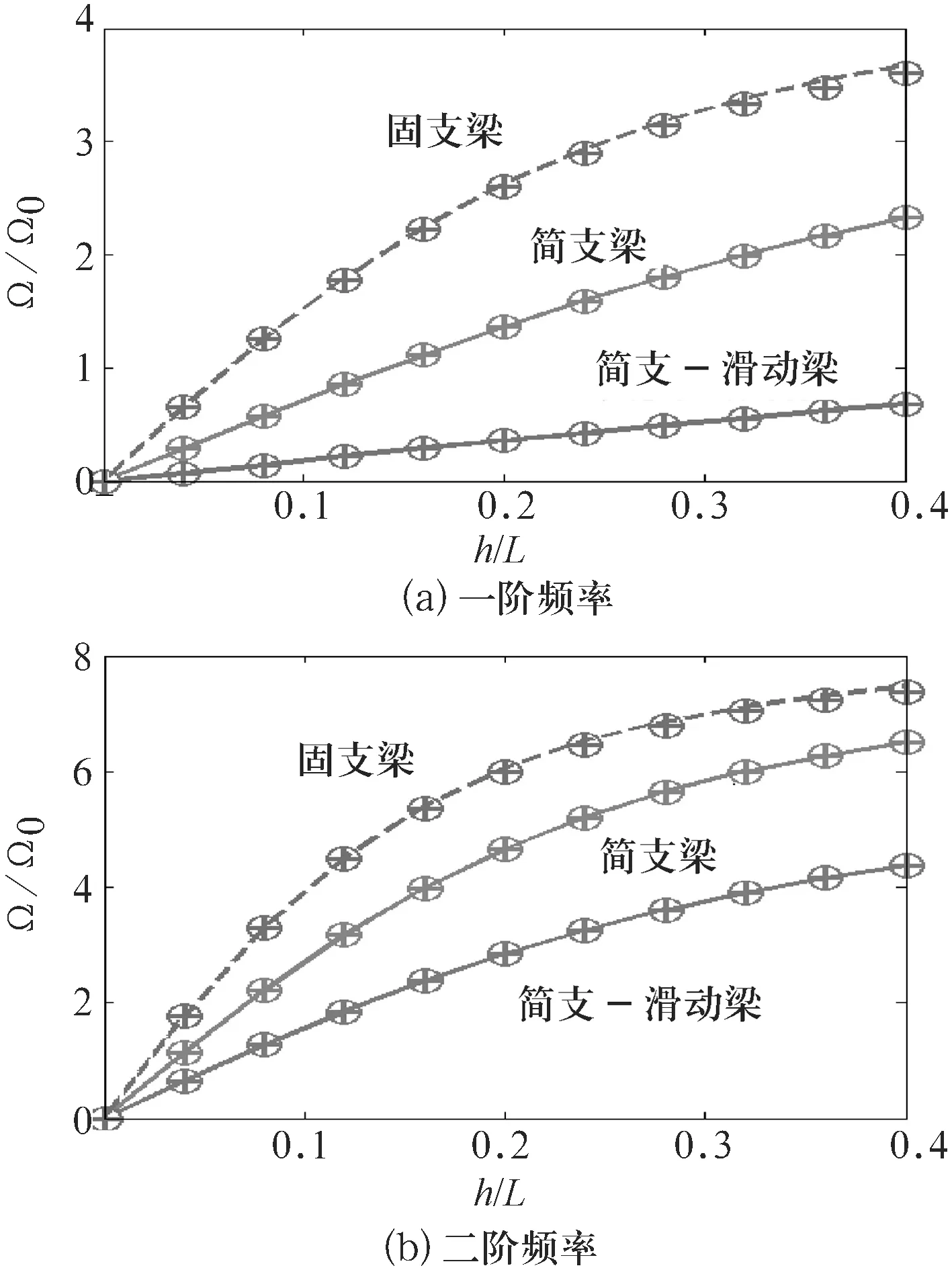
圖2無軸力時無量綱頻率的對比
由圖2可知,簡支梁、簡支—滑動梁和固支梁不考慮軸向力時,前兩階模態的無量綱頻率Ω/Ω0隨高跨比h/L的變化結果(標識)與參考文獻[9](實線)和數值模擬得到的結果(虛線)一致.值得注意的是,由于此時軸向力不存在,躍遷系數α對固有頻率沒有影響.
2)考慮軸力時,無量綱頻率的對比情況如圖3所示.
在圖3中考慮了軸力的影響,無量綱頻率隨著軸向力的大小變化而變化,明顯得出α=0對應的本研究結果與文獻[9]給出的解以及有限元模擬值是一致的.這是因為文獻和ANSYS軟件都是假設梁處于變形過程中,軸向力的作用方向與變形層中性軸相切(即,α=0的情況),當軸向力接近于臨界屈曲力時,基頻趨近于0.
2.2 軸向力對自由振動的影響
無量綱頻率隨無量綱軸向力的變化(h/L=0.3)如圖4所示.
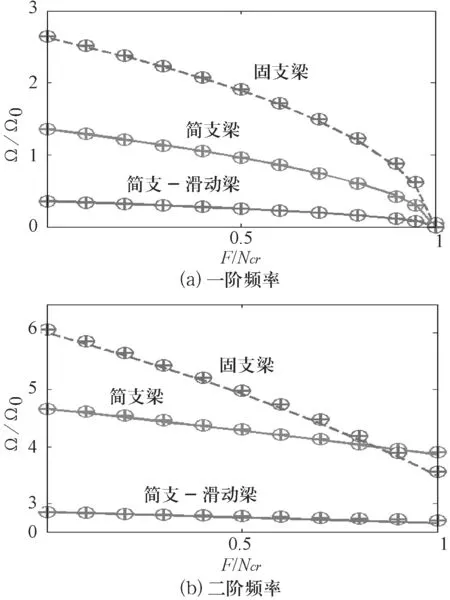
圖3考慮軸力時無量綱頻率的對比
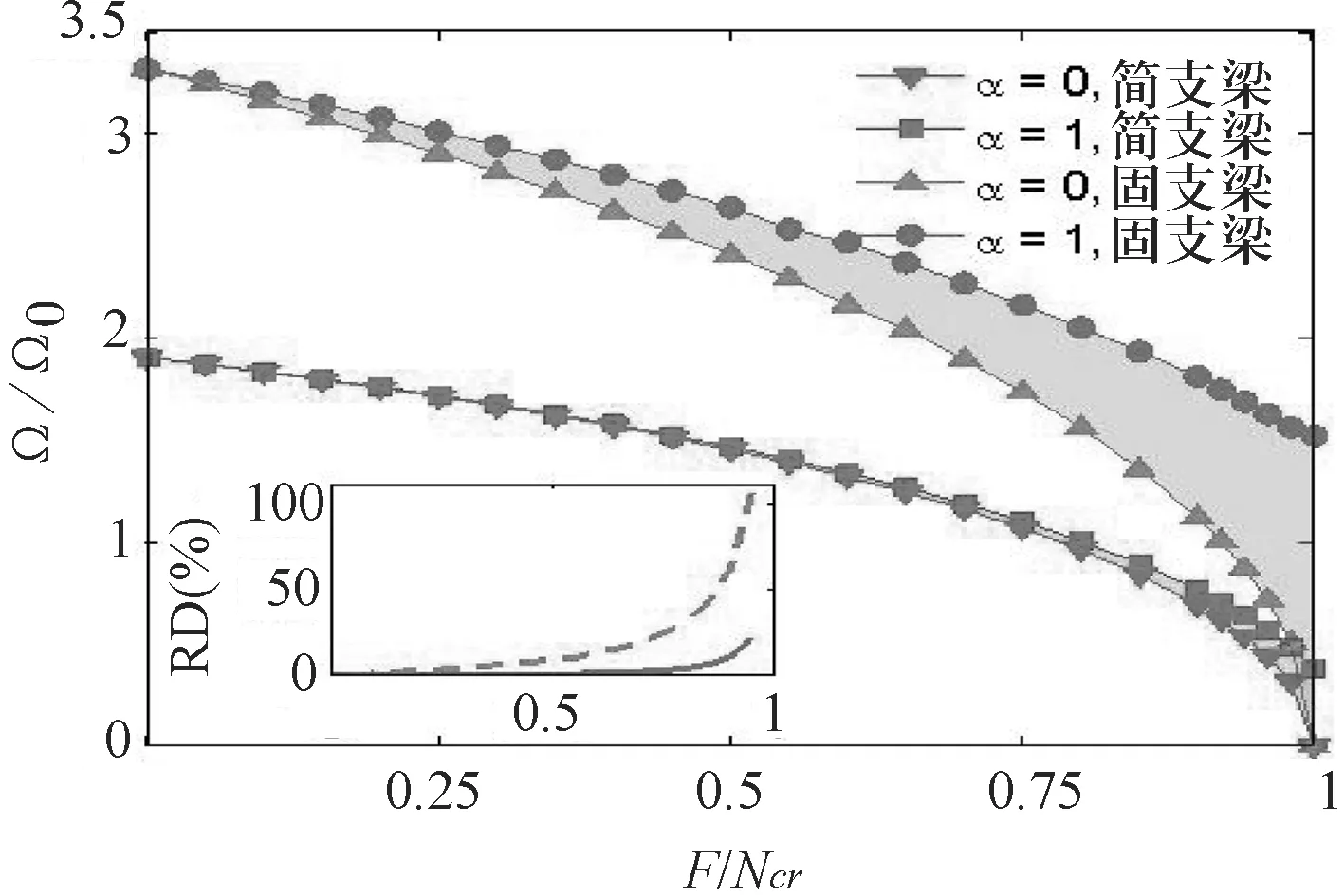
圖4無量綱頻率隨無量綱軸向力的變化(h/L=0.3)
由圖4可知,給定高跨比h/L為0.3的梁,其固有頻率在軸向載荷作用初期,頻率降低得較慢,隨著軸向載荷的增加,基頻的衰減量逐漸變大,最后當軸向力達到臨界屈曲力時,基頻衰減到0.
圖4中陰影區域表示α=0和α=1之間的頻率差距.為了直觀地分析躍遷系數的影響,定義相對誤差RD=(Ωα=0-Ωα=1)/Ωα=0×100%.可以看出,躍遷系數α對固支梁的影響比簡支梁大得多,這是因為軸向力在變形時對固支梁的剪力貢獻比對簡支梁的剪力貢獻大.
2.3 高跨比對自由振動影響
無量綱高跨比的變化對無量綱頻率的影響如圖5所示.
由圖5可知,考慮軸力F=0.8Ncr的固支鐵木辛科梁的躍遷系數對自由振動的影響和高跨比h/L成正比,且躍遷系數對固支梁的影響較大.在較為極端的情況下(h/L=0.4),固支梁的相對誤差RD=49.49%,即躍遷系數對固支鐵木辛科梁的影響非常顯著.
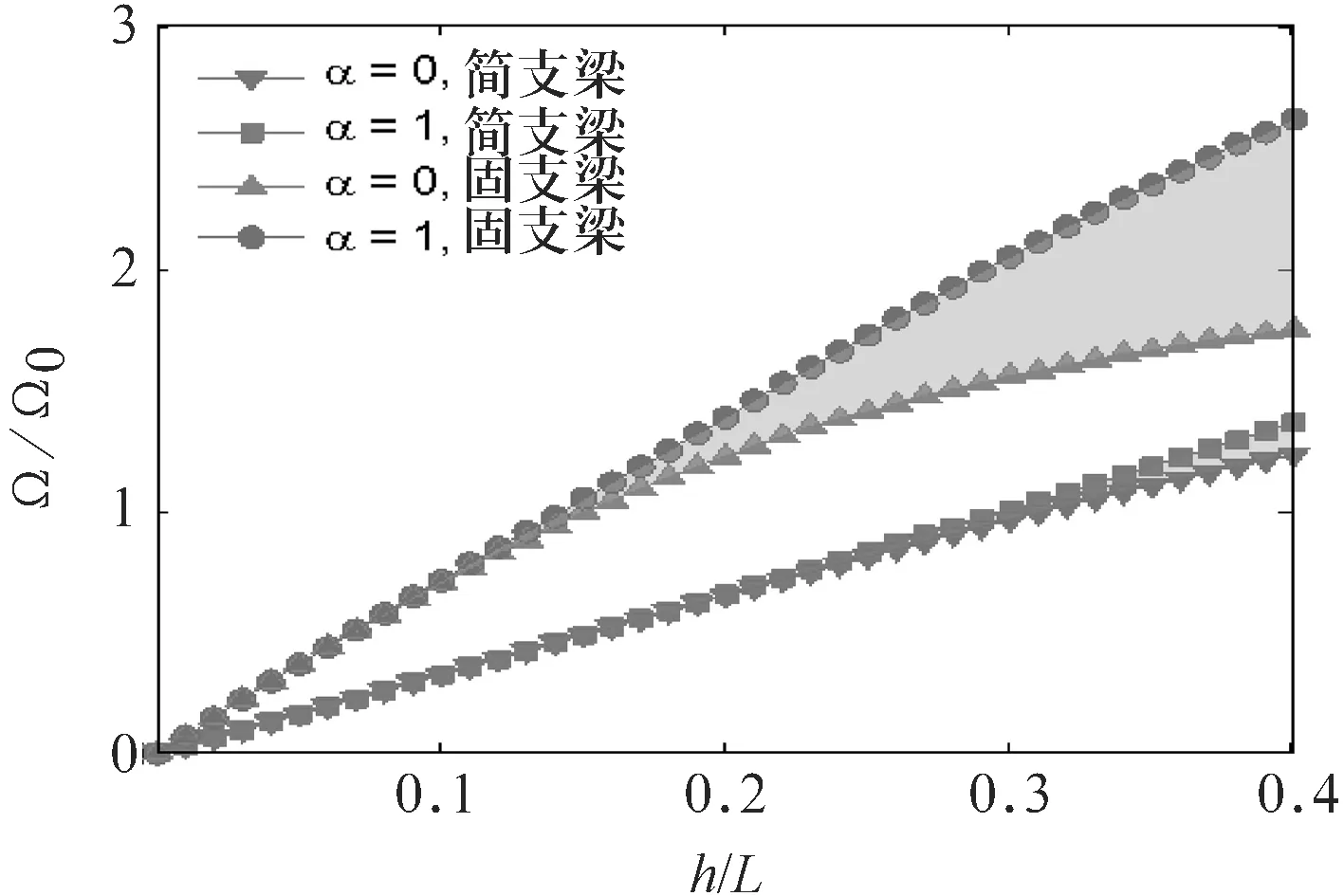
圖5無量綱頻率隨無量綱高跨比的變化
3 結 論
本研究利用包含躍遷系數的統一模型推導了多種邊界條件下軸向受力鐵木辛科梁的頻率方程,利用數值模擬驗證了結果的正確性.通過對比躍遷系數取0和1的情況發現,在考慮軸向力作用方向時,在較大的軸向力和高跨比的取值的情況下,躍遷系數對梁的自由振動的影響更顯著.在數值模擬中,本研究發現躍遷系數對固支梁的自由振動有顯著的影響,而對簡支梁的影響較弱.在F=0.8 Ncr,h/L=0.4時,兩種經典軸力方向對應的固支鐵木辛科梁的相對誤差可達到49.49%.

