含多耦合故障的轉子系統的響應分析
伍小莉, 楊 洋, 葛玉梅
(西南交通大學 力學與工程學院, 四川 成都 610031)
0 引 言
隨著現代機械工業的快速發展,旋轉機械也在向高轉速、高效率的方向發展.由于一些不可避免的因素,使得旋轉機械會出現各種各樣的故障,降低了旋轉機械的性能,有時候還會導致機器永久性的破壞,甚至發生機毀人亡的事故[1].而在旋轉機械的各種故障中,不對中及碰摩是極為常見的情形.不對中故障一般可分為平行不對中、角度不對中及綜合不對中.據相關資料顯示,約70%的機械振動故障是由軸系不對中引起或與之相關[2].針對此情況,科研人員進行了相關的研究,并取得了一系列成果[3-7].在此基礎上,本研究以某旋轉機械轉子系統為分析對象,利用數值仿真的方法分析了具有不平衡—不對中—碰摩耦合故障轉子系統的動力學特性,并討論了平行不對中程度與碰摩間隙對其動力學行為的影響規律.
1 不對中—碰摩耦合故障下轉子的動力學模型
1.1 動力學方程
本研究建立的考慮轉盤質心和形心不同心,且存在平行不對中—碰摩耦合故障的轉子系統的動力學模型如圖1所示.
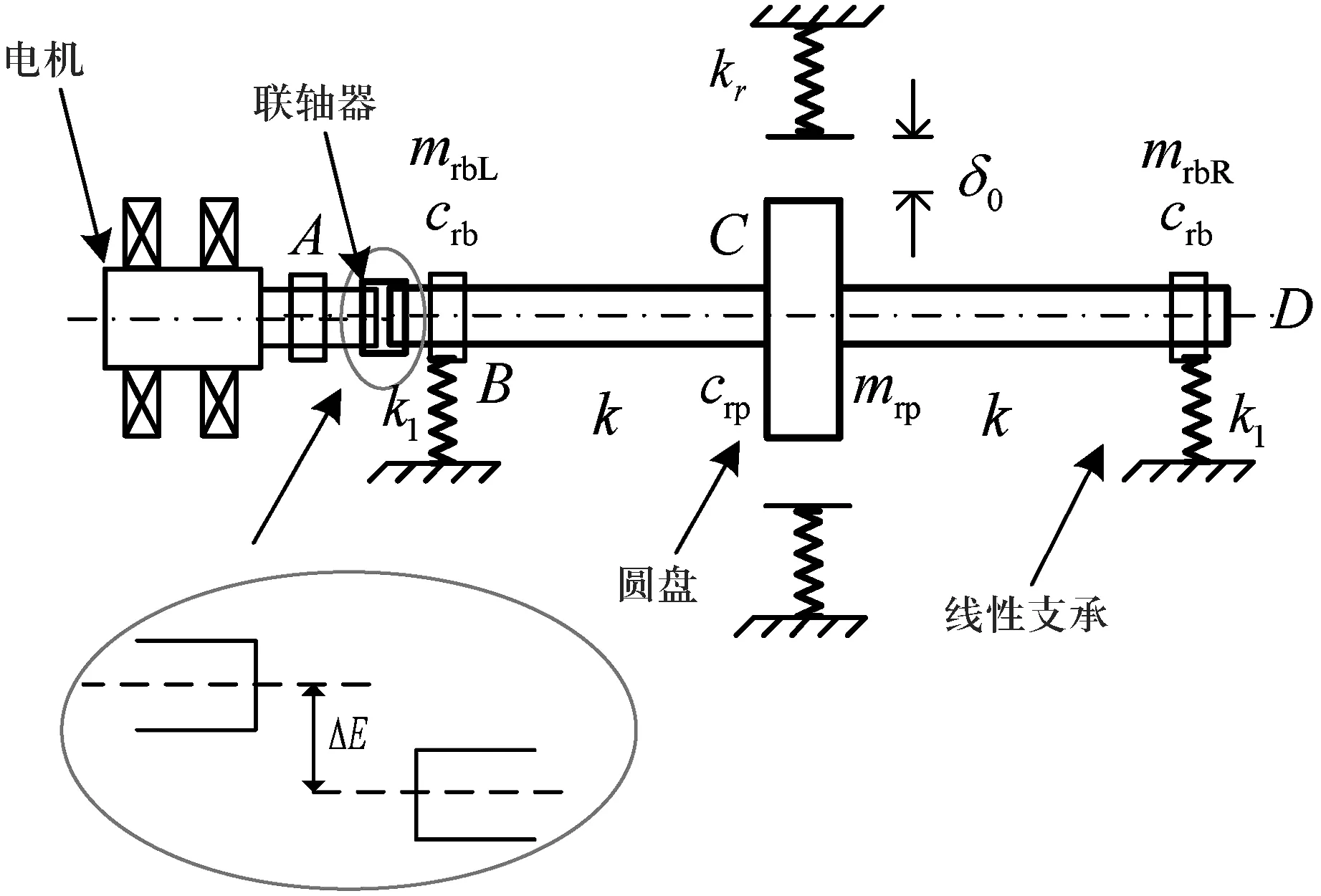
圖1轉子系統動力學模型示意圖
在圖1模型中,左側部件為一電機,它與右側轉子通過聯軸器連接.此處,令mrp為轉盤的等效質量,mrbL、MrbR分別為左端線性支承和右端線性支承處的等效質量,k1為兩端線性支承的剛度,k為轉盤左右兩彈性軸的剛度,kr為轉盤處的碰摩接觸剛度,crp為轉子在轉盤處的阻尼系數,crb為軸承處的阻尼系數,ΔΕ為轉子平行不對中量,e為轉盤質量偏心量,mc為聯軸器齒套的質量,δ0為轉子和靜子部件間的初始間隙,f為轉子與靜子部件間的摩擦系數.
該動力學模型中,共有6個自由度,分別為:轉盤的橫向自由度xrp和豎向自由度yrp,左端軸承有橫向自由度xrbL和豎向自由度yrbL,以及右端軸承處的2個自由度xrbR、yrbR.
轉子系統的動能、勢能和耗散函數分別為,
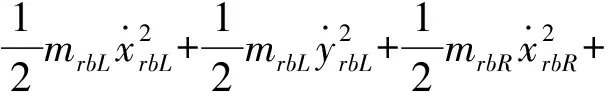
(1)
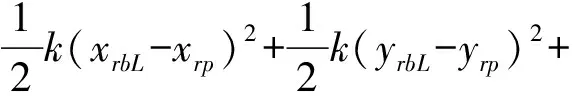
(2)
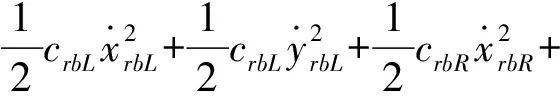
(3)
耗散系統的Lagrange方程為,
(4)
式中,L為Lagrange函數,L=T-V,T為系統總動能,V為系統的勢能,Qj是廣義力.
將式(1)~(3)代入式(4),可得,
(5)
式中,FxL、FyL、FxR、FyR為左右兩端線性支承處的支承力,Px、Py為不對中產生不對中激振力在x、y方向的分力,Fx、Fy為由于碰摩故障產生的碰摩力在x、y方向的分力.
1.2 不對中模型
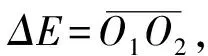
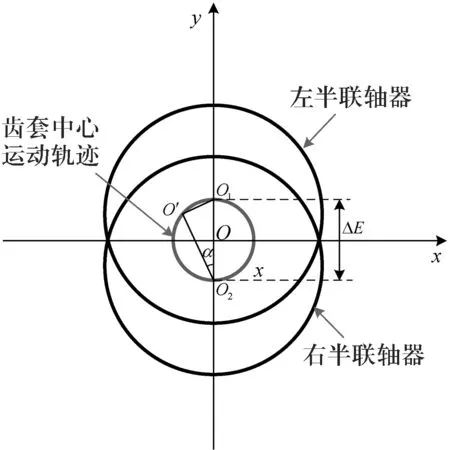
圖2不對中模型示意圖
齒套中心O′的運動軌跡表示為,
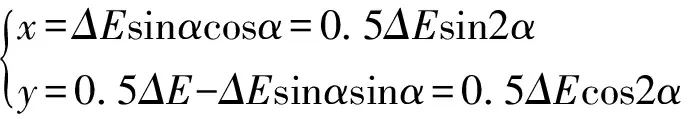
(6)
將式(6)對時間t求2階導數,以此得到O′的加速度為,
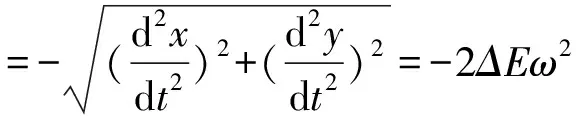
(7)
由于聯軸器的質量較大,因此轉子存在平行不對中故障時,相當于給轉子施加了一個不對中激振力,激振力PO′及激振力在x、y方向上的分力Px、Py分別為,
PO′=-2mcΔEω2
(8)
(9)
式中,mc為聯軸器齒套的質量,ΔE為聯軸器的平行不對中量.
1.3 碰摩力模型
轉子系統的碰摩力模型如圖3所示.圖3中,碰摩力分為徑向碰摩力Fn和法向碰摩力Fτ.假設摩擦符合庫侖摩擦定律,將碰摩力分解在x和y軸上,可以得到在x和y方向的碰摩力為,
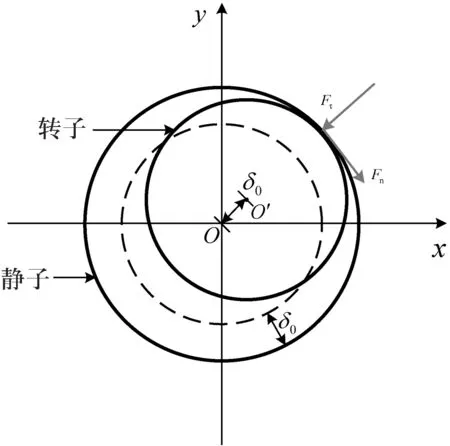
圖3碰摩力模型示意圖
(10)
2 仿真計算與分析
本研究利用龍格庫塔法[8]對模型進行數值仿真與分析.轉子系統的主要參數為:mrp=32.1 kg、mrbL=mrbR=4 kg、mc=2.61 kg、k=2.5×107N/m,kr=3.5×107N/m、k1=1.1×108N/m、crp=2 100 N·s/m、crb=1 050 N·s/m、e=0.01 mm、f=0.1.
2.1 碰摩故障的發生對系統動力學特性的影響
當轉子系統高速運轉時,不對中可能會誘發碰摩故障的產生.為了對比不對中故障未誘發碰摩故障與誘發碰摩故障這兩種情況的動力學特性,分析了無故障轉子、不對中量ΔE=0.2 mm且不發生碰摩以及不對中量ΔE=0.2 mm且碰摩間隙δ0=0.02 mm這3種狀態下轉子系統的幅頻曲線.仿真結果如圖4所示.

圖4 3種狀態下轉速—轉盤橫向位移圖
從圖4可以看出,由于不對中故障,系統在約臨界轉速二分之一的附近出現了突起,即不對中故障會引發系統在約二分之一臨界轉速處振動加劇.此外,與不對中故障未誘發碰摩故障相比較,當不對中誘發碰摩故障時,系統的臨界轉速增大,且在臨界轉速處的轉盤的橫向位移由于碰摩的發生有所下降,當轉速到達二分之一臨界轉速時,由于碰摩的發生,轉盤的響應會出現一個突降.
2.2 不對中量對不對中—碰摩耦合故障下轉子系統動力學特性的影響
轉子系統在不對中故障和碰摩故障相互耦合作用下,會由于這種耦合故障的產生導致聯軸器的不對中量在運轉過程中發生改變.為研究在不對中—碰摩故障耦合下,不對中量對系統響應的影響,分析了在轉靜間隙為δ0=0.01 mm,分別取不對中量為0.2 mm、0.3 mm及0.4 mm時,轉盤隨著轉速增加,其橫向位移的變化趨勢.仿真結果如圖5所示.
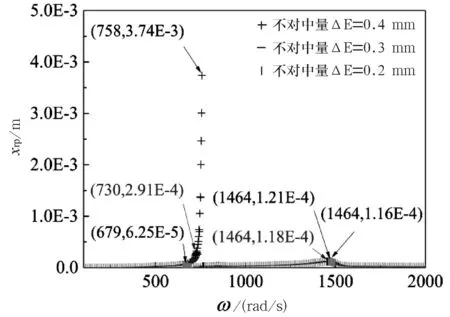
圖5不同不對中量下的轉速—轉盤橫向位移圖
從圖5可以看出,隨著不對中量的增加,轉盤在轉速到達臨界轉速時,橫向位移呈現增加的趨勢.此外,由于不對中所產生的在約二分之一臨界轉速的突起會隨著不對中量的增加,突起的最高點會呈現一個往后移動的趨勢.
2.3 轉靜間隙對不對中—碰摩耦合故障下轉子系統動力學特性的影響
當轉子系統發生不對中—碰摩耦合故障時,在運轉過程中由于碰撞摩擦等因素可能會導致轉靜間隙發生改變.為研究轉靜間隙的改變對不對中—碰摩耦合故障下轉子系統動力學特性的影響,分析了在不對中量ΔE=0.2 mm,轉靜間隙取0.01 mm、0.015 mm、0.02 mm時,轉盤隨著轉速增加,其橫向位移的變化趨勢.仿真結果如圖6所示.
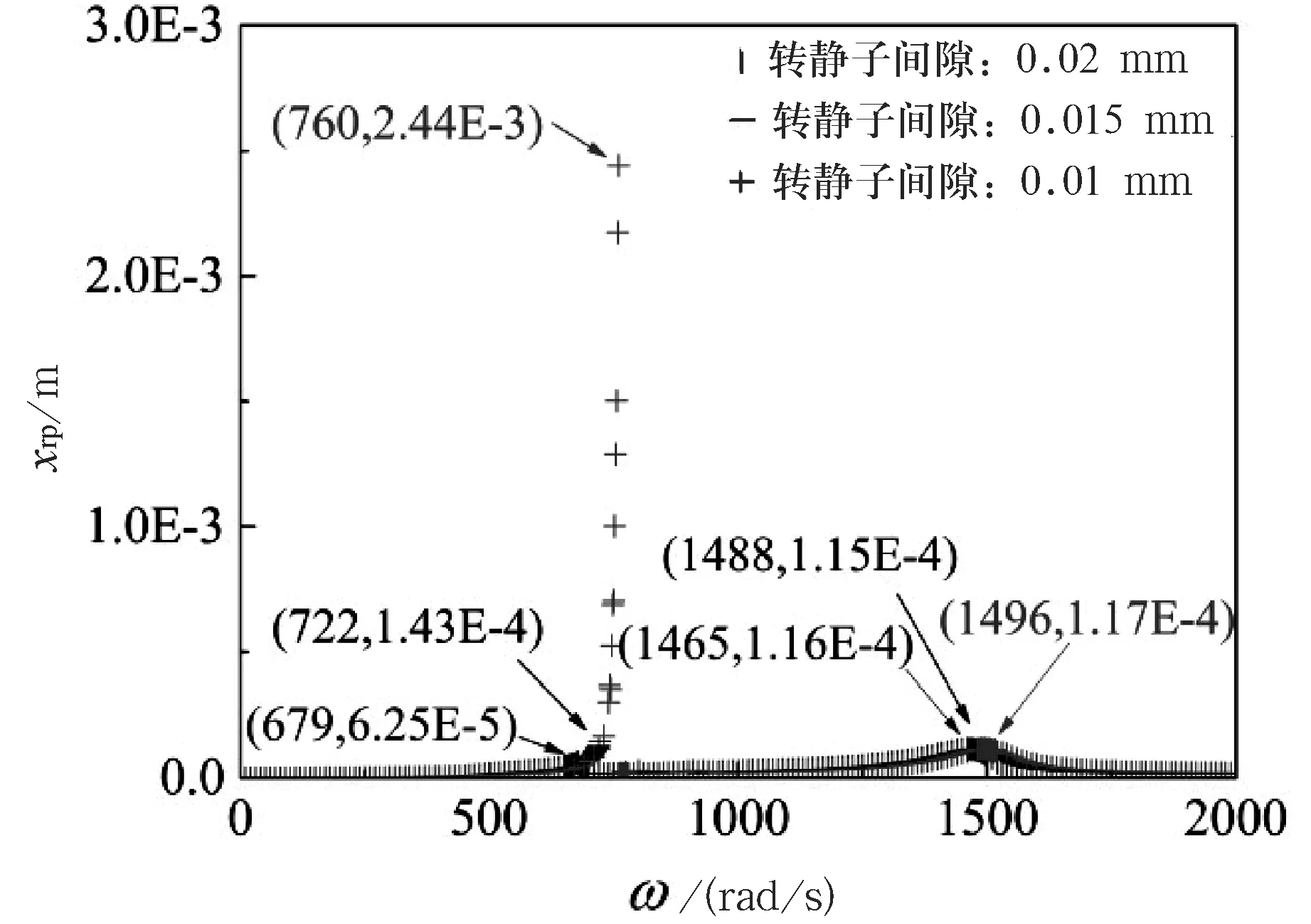
圖6不同轉靜間隙下的轉速—轉盤橫向位移圖
從圖6可以看出,隨著轉靜間隙的增大,臨界轉速隨之減小,且臨界轉速對應的橫向位移越來越小.此外,當轉速到達二分之一臨界轉速附近時,由于轉靜間隙的增大,系統對應于最大橫向位移的轉速越來越大.
3 結 論
本研究通過對一多耦合故障的轉子系統的動力學特性的分析,得出如下結論:與不對中未誘發碰摩故障對比,當轉子系統的不對中故障誘發碰摩故障后,系統的臨界轉速與臨界轉速對應的橫向位移增大,且在二分之一臨界轉速的位置由于碰摩故障的發生會出現突降現象;隨著不對中量的增加,不對中—碰摩耦合故障下轉子系統的臨界轉速與臨界轉速對應的橫向位移增大,且在約二分之一臨界轉速突起最高點的位置的轉速和橫向位移越來越大;隨著轉靜間隙的增大,不對中—碰摩耦合故障下轉子系統的臨界轉速與臨界轉速對應的橫向位移減小,且在約二分之一臨界轉速突起最高點的位置的轉速和橫向位移越來越小.

