《數學實驗手冊》 在“五步法數學教學”中的實踐應用研究

黃豐蘭

[摘? 要] 《數學實驗手冊》為初中數學教學提供了新型的教學資源，文章從“五步法數學教學”三大課型（新授課、復習課、實驗課）入手，將《數學實驗手冊》和課本有機結合，選取實驗對象，設計實驗內容，全面激發學生的數學學習興趣，引導學生進行觀察、探索、猜想、驗證，從而獲得數學理解，實現數學學科能力和素養的全面提升.

[關鍵詞] 初中數學實驗手冊;深入理解;數學情感;空間想象;實踐推理

傳統的數學教學常以“教師講，學生聽”的方式為主，在講解過程中，教師會追尋知識的來源，但大多或以呈現為主，或把數學知識發現的過程簡約化，使學生在感知與概括之間出現思維斷層，這不利于學生創造性思維的培養.

數學家歐拉說過，數學這門學科需要觀察，也需要實驗. 《義務教育數學課程標準（2011年版）》指出：為了幫助學生真正理解數學知識，教師應注重數學知識與學生生活經驗的聯系，與學生學科知識的聯系，組織學生開展實驗、操作、嘗試等活動，引導學生進行觀察、分析、抽象概括、運用知識進行判斷. 基于以上理論，初中數學實驗研究小組根據初中教學內容，精心編制了《初中數學實驗手冊》（以下簡稱《手冊》），共涉及65個實驗，其目的便是引導學生利用數學實驗，探索數學知識，提高學生的學習水平. 本文結合筆者的教學經驗，就如何利用《手冊》應用于“五步法數學教學”，做了以下探索.

《手冊》在“五步法數學新授課”

中的主要應用

列夫·托爾斯泰曾說：知識，只有當它靠積極的思維得來，而不是憑記憶得來的時候，才是真正的知識. 學習概念、性質時，學生往往只對概念、性質進行記憶，而對概念、性質的本質屬性理解不夠，這種一知半解的情況，造成了諸多的知識漏洞. 為了讓學生真正掌握概念及性質，教師可充分、合理地利用《手冊》，引導學生細心觀察，感知表象;動手探索，大膽猜想;交流思考，概括總結，實現對概念及性質的深入理解.

如講解無理數的概念時，許多教師都會直接告知學生：無限不循環小數是無理數，常見的無理數有以下兩種形式：一是無限不循環小數，如π，2.010010001…;二是開方開不盡的數，如. 這種教學方式只對概念進行了記憶，缺少了對概念的感知過程. 教師可利用《手冊》設計實驗，先讓學生把分數化為小數，通過觀察其小數點后的數字，發現分數都可以化為有限小數或無限循環小數;其次，通過擲骰子寫小數的游戲方式，及利用Excel軟件產生隨機小數，體會無限不循環小數的真實存在性;隨后，通過構造2.010010001…這樣的小數，進一步體會無限不循環小數的客觀存在性;最后，通過拓展活動，了解圓周率也是無限不循環小數，從而讓學生感知和體驗無理數概念的形成過程，深入理解無理數的概念.

再如，探索勾股定理時，按《手冊》可設計四步教學過程：首先，運用全等三角形的知識和割補圖形的方法，利用方格紙設計計算格點正方形ABCD的面積;其次，通過方格紙上的操作、實驗，探索分別以格點直角三角形的三邊為邊長的三個正方形的面積與直角三角形三邊長之間的關系，感受數形結合思想;再次，用上述方法完成四組不同圖形面積的相關計算，并在上述操作的基礎上，猜想直角三角形三邊之間的關系;最后，化特殊為一般，通過構造圖形加以驗證，歸納得出勾股定理. 這一系列的操作過程，能讓學生經歷觀察—猜想—歸納—驗證的發現過程，能把抽象的數學問題通過直觀的背景呈現出來，能幫助學生抓住本質，實現對勾股定理的接受和理解.

《手冊》在“五步法數學復習課”

中的主要應用

“五步法數學復習課”不是舊知識的簡單再現或機械重復，而是學生在教師的引導下，梳理知識體系，把學過的零碎知識系統化，在應用舊知的同時，有新知識、新方法的再生成和再創造. 在此課型中設計數學實驗，不但能提高學生上復習課的興趣，而且能在體驗、發現、創造的過程中，激發學生的空間想象能力，提高學生的數學實踐推理能力和綜合應用能力. 復習課中設計的數學實驗主要有如下三類：

1. 生活情景類活動——主在促進學生的數學情感體驗

數學來源于生活，又服務于生活. 教學時，教師引導學生把數學知識和生活實踐聯系起來，如天平與等式、不等式之間的聯系，鐘面上數字所夾的角度等，讓學生在所設計的生活情景實驗中探索數學知識，這樣所獲得的知識無疑是深刻的、牢固的. 這種生活情景類實驗，能讓學生體會到數學知識是看得見、摸得著的，能寓學于樂，提高學生學習數學的興趣. 同時，在學生獨立思考的同時，能加強學生與學生、學生與教師之間的合作與交流，在成功的體驗中、同學的肯定中、教師的表揚中，學生也會有一系列的情感體驗.

2. 勞技制作類實驗——主在培養學生的空間想象能力

有些數學知識的掌握需要學生有一定的空間想象能力，教師在教學過程中，可引導學生動手操作，通過折、剪、拼等方式，制作幾何體實物或模型，在操作的過程中，讓學生感知平面圖形與立體圖形之間的轉換，或從實物模型轉換至數學模型，發展學生的空間觀念.

如學習“展開和折疊”這節內容后，我們都會對正方體的展開圖進行適當拓展. 但教師為了節約時間，往往會直接和學生簡單地商量出正方體的11種展開圖，并以口訣的形式傳授給學生. 其實，教師可以利用《手冊》開展“展開與折疊”這一實驗：首先，通過畫、剪、折來研究幾何圖形，從折疊無蓋的盒子到折疊成正方體，再到折疊成標有字母的正方體，讓學生初步感受平面圖形和立體圖形之間的關系;其次，在想象的基礎上，通過動手操作，理解復雜的平面圖形的折疊，實現從“無序”到“有序”的轉變;最后，在前面環節的鋪墊下，想象正方體盒子的平面展開圖，進一步體會立體圖形與平面圖形之間的關系. 這樣的教學方式，能有效地培養學生的空間想象能力，達到“授之以魚，不如授之以漁”的效果.

3. 圖形變換類操作——主在提高學生的實踐推理能力

初中數學常見的變換形式有三類：對稱、翻折、旋轉. 教學時，教師常用幾何畫板軟件呈現圖形的變換過程，從而讓學生發現點的運動軌跡或圖形的基本特征. 但學生平時解決問題時，沒有幾何畫板這一輔助工具，故課堂上學生觀察幾何畫板呈現的變換就如同看雜技表演，在感嘆其形象化的同時，并沒有掌握解決問題的方法. 此時，教師可以先讓學生動手實驗、探索猜想，結合幾何畫板軟件對猜想進行驗證，找到解決問題的方法. 雖然這樣操作會耗費一定的時間和精力，但在操作的過程中，隨著實踐操作、提出問題、分析問題、解決問題，學生的推理創新能力定能得到培養和提升.

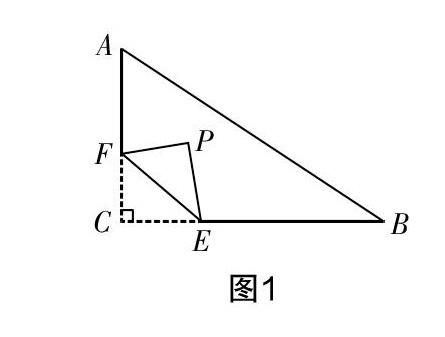
例如，如圖1，在Rt△ABC中，∠C=90°，AC=7，BC=8，點F在邊AC上，且CF=2，點E為邊BC上的一個動點，將△CEF沿直線EF翻折，點C落在點P處，則點P到邊AB距離的最小值是多少？

該題屬于圖形的翻折問題，探索時可讓學生按題意進行操作，在翻折的過程中，發現點C翻折后產生的運動軌跡為圓，從而得出定點加定長產生隱形圓的基本模型，此時題目便已轉化為在定圓上找一點，使它到定線段距離最短的問題. 在實驗中，教師幾何畫板的操作僅為輔助工具，學生的探索才是主體. 隱形圓的運動軌跡是由學生自主實驗探索得到的，故他們能夠深刻理解、透徹掌握此模型的條件、結論、原理和依據，這有助于深化數學應用意識.

《手冊》在“五步法數學實驗課”

中的主要應用

《手冊》作為初中數學教材的補充和輔助，其實驗操作多數安排為課堂教學中的一個環節，以幫助學生進行學習. 但如“七巧板拼圖”這一數學實驗，教材中的說明“惜字如金”，但它作為“5.2 圖形的變化”教學內容的一部分，卻有著一定的意義和作用. 對于這類實驗，教師可根據教學情況，充分利用《手冊》，設計成“五步法數學實驗課型”進行教學，幫助學生拓寬知識面，重視數學發現、數學創造的過程，從而提高學生的數學素養.

如在“七巧板拼圖”授課中，教師可先安排學生查閱與交流七巧板的歷史，讓學生了解祖先的智慧以及數學對社會發展、人類進步起到的巨大作用;其次，在學生逐步認識七巧板、拼拼七巧板、創意七巧板的實驗活動中進行思考、探索、交流，激發學生的學習熱情，提高學生的創新能力，感受空間圖形與現實生活之間存在的密切聯系，并進一步體會數學的無窮魅力.

《數學實驗手冊》為初中數學教學提供了一個新型的教學資源. 教師在教學過程中，不要全盤照搬，而要深入研究教材，根據實際情況，選取適當的實驗對象，設計恰當的實驗內容，與課本有機結合，融入和分解到日常教學中，幫助學生在活動中獲得感性認識和相應經歷，通過分析概括、推理演繹，獲得數學理解，在全面激發學生數學學習興趣的基礎上，實現學生數學學科能力和素養的全面提升.