仿生機器魚尾鰭推進效率的多參數優化研究?

張開升， 楊明明， 王 強， 張保成

(中國海洋大學工程學院機電工程系, 山東 青島 266100)

魚類作為地球上出現最早的脊椎動物，經過數億年的自然選擇，進化出了非凡的水中運動能力，其游動具有推進效率高、機動性強、隱蔽性好、噪聲低、對周圍環境擾動小等優點[l]。正是魚類這些運動特點啟發機器人學者，通過模仿魚類的運動方式，不斷研制和完善具有魚類運動特點的仿生機器魚，以期構建采用高效、高機動游動方式的新型水下機器人系統。國內外學者越來越重視仿生機器魚的研究與開發，并取得了很多階段性成果。但是，目前仿生機器魚的推進效率與自然魚類仍相差較遠[2-3],僅僅對尾鰭單一參數進行優化，無法實現高效推進。哈爾濱工業大學的王冉冉[4]通過基于三坐標系的仿魚機器人穩態游動速度求解算法，分別研究魚體的振幅、頻率、尾鰭最大擊水角度等參數對推進效率的影響，得出最大的推進效率只有33%；中國科學技術大學的陳宏[5]，通過Froude游動效率仿真，得出的最好平均效率為0.58；弗吉尼亞理工學院的A K Kancharala 和M K Philen[6]對尾鰭水動力性能進行了研究，得到的最大推進效率只有45%。這些研究成果相比于自然界中魚類90%左右的推進效率相去甚遠。

本文針對目前仿生機器魚優化推進效率的研究現狀，提出對尾鰭推進進行多參數優化的思路，使各參數相互配合，以接近自然魚類的真實游動，從而使仿生機器魚達到較高的推進效率。

1 尾鰭運動參數

尾鰭的運動實質是由多個簡單的動作復合而形成的，其中包括平動和轉動，而每個簡單的動作又可以用不同的參數進行描述。本文將尾鰭的復雜運動分解為以下幾個參數[6-7]來進行多目標優化。

1.1 轉動頻率

尾鰭轉動頻率ω(Hz)，描述尾鰭繞尾柄轉動的快慢。O點為尾柄，轉動頻率的定義如圖1所示。

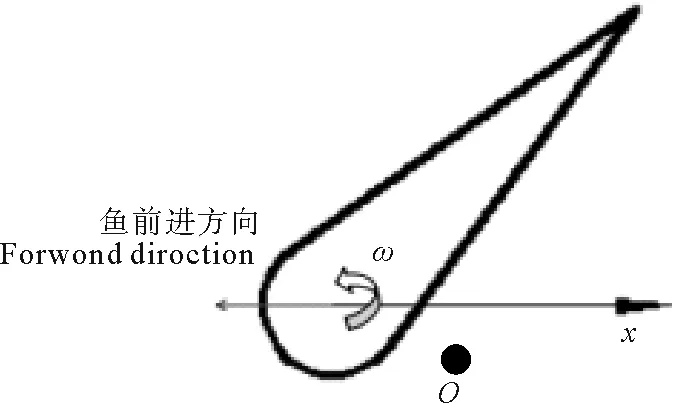
圖1 轉動頻率示意圖

1.2 擺動幅值

尾鰭的擺動幅值H(m)，描述尾鰭隨尾柄往復擺動的最大距離。

1.3 最大擊水角度αmax

尾鰭的擊水角度α(Deg)，為尾鰭中心線與尾柄軌跡切線間的夾角，如圖2所示。其中最大擊水角度αmax是尾鰭擺動幅值為0時，尾鰭中心線和尾柄軌跡切線間的夾角。擊水角度對推進力和側向力的方向變化起著重要的作用，在不同的游速下，最大擊水角度各不相同。由于尾鰭在運動過程中擊水角度隨時發生變化，因此本文用最大擊水角度αmax描述其對推進效率的影響。

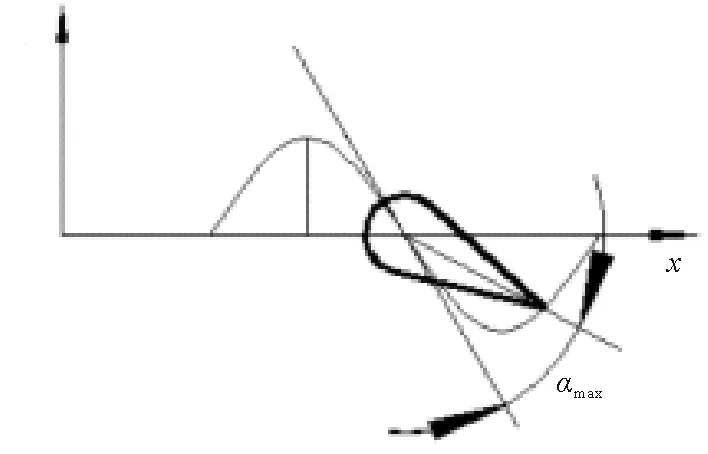
圖2 尾鰭最大擊水角度示意圖

1.4 擺動周期

尾鰭的擺動周期T(s)，描述尾鰭隨尾柄由初始位置經過一次往復擺動恢復到原位置所用的時間。尾鰭的擺動是一個復合運動，即尾鰭轉動與y軸方向尾柄平動的合成運動，因而其擺動周期與轉動周期不同，如圖3所示。

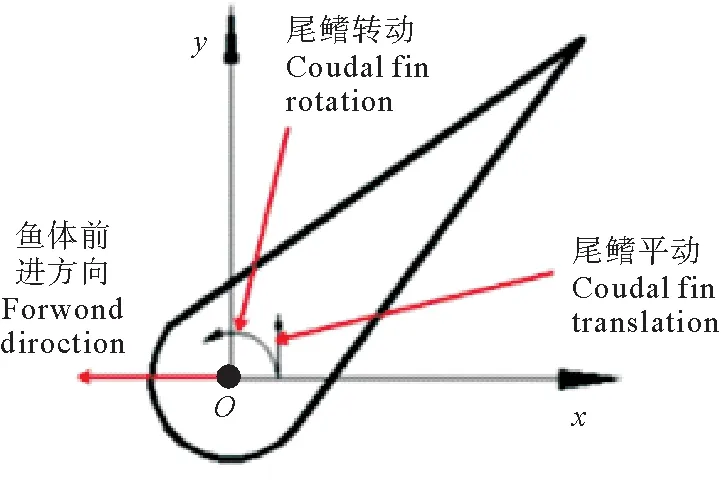
圖3 尾鰭擺動示意圖

2 以推進效率為目標的多參數優化設計

2.1目標函數

推進效率是仿生機器魚研究的重要指標，它是衡量仿生機器魚推進性能的關鍵參數，因此，本文研究仿生機器魚在巡游狀態下的推進效率，以此建立目標函數，在前人研究的基礎上，提出一種新的優化方法。

魚類在游動過程中，其有用功是由尾鰭產生的推進力提供的，而無用功則是由側向力產生的，因此其推進效率計算公式可以定義為：

(1)

式中：WT為推進力作功；WF為側向力作功。

根據前人成果，可以計算尾鰭上的升力和阻力，其計算公式如下：

(2)

式中：ρ：流體密度；VC：尾鰭速度；CL：升力系數；CD：阻力系數；S：尾鰭面積 。其中，VC是3個速度的合成，包括尾鰭轉動速度V1，尾柄平動速度V2和魚體前進速度u，即VC=V1+V1+u。

則尾鰭在x(魚體前進方向)和y(垂直于魚體前進方向)方向的受力為：

(3)

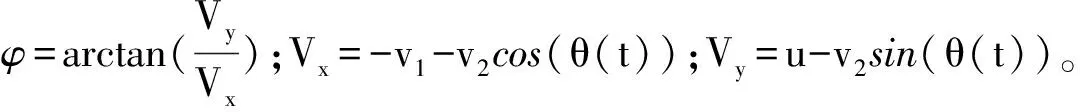
其中：Vy為尾鰭速度在y方向的分量；Vx為尾鰭速度在x方向的分量，其表示如圖4所示。

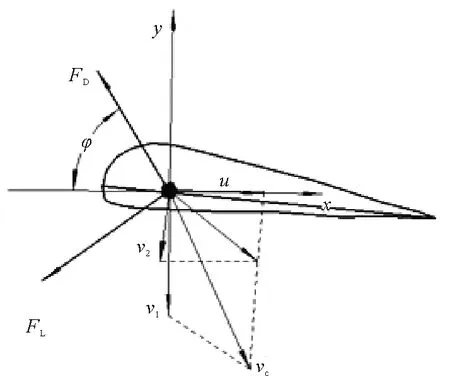
圖4 φ角示意圖

則尾鰭瞬時產生的有用功率和側向功率是：

(4)

從而得到運動周期內的平均效率為：

(5)

文中關于尾鰭的參數數據來源于作者所在科研團隊的前期研究成果[9]，其中，尾鰭面積S=5×10-3m2，尾鰭的弦長：l=45 mm。

2.2 約束條件

本文依據目前單一優化推進效率的參數所得到的結果，再結合本文具體的模型，給出了適合本文的參數變化范圍。

2.2.1 轉動頻率 目前對仿生機器魚推進力及推進速度的研究中，選擇的擺動頻率一般在5 Hz以下，本文將轉動頻率的取值范圍設為ω∈[0,10]。

2.2.2 擺動幅值 魚類在游動過程中，其擺動幅值要受到體長(L)的限制，擺動幅值一般不會超過體長的20%，本文所用模型體長為L=0.69 m，因此擺動幅值的范圍是H∈[0，0.2L]。

2.2.3 擺動周期 由于本文模型的擺動幅值和優化時所選游速的限制，因此擺動周期的取值范圍是T∈[0，20 s]。

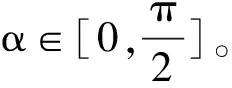
2.3 優化求解及結果分析

2.3.1 優化求解 本文采用遺傳算法進行目標函數的優化。

2.3.1.1 編碼 由于二進制編碼方式簡單，便于實現交叉、變異等遺傳操作，本文采用24位的二進制編碼方案對參數進行編碼。

2.3.1.2 產生初始種群 本文選擇初始種群的個體數目為200個。

2.3.1.3 計算適應度 本文所優化的目標函數為效率的最大值，所以直接引用目標函數作為適應度函數。

2.3.1.4 遺傳操作 本文采用錦標賽選擇法；交叉操作采用二進制單點交叉，交叉率為0.9；變異操作采用二進制單位變異，變異率是0.1。

2.3.1.5 收斂條件 本文的終止進化代數設定為80代。

2.3.2 優化結果及分析 魚類穩態游動時游速通常不高，且目前對仿生機器魚進行效率優化時游速的取值也在1 m/s以下，因此本文分別取游速為0.2L、0.4L、0.6L、0.8L、1L、1.2Lm/s進行參數優化，得到在某一特定游速下的最佳參數取值。本文將所得幅值H換算成體長的倍數，以便得到幅值與體長的關系。得到的參數優化結果如表1所示。

據此，其推進效率與巡游速度的關系如圖5所示。

從圖5可以看出尾鰭推進效率和游速之間的關系，游速在0.2L～0.6Lm/s之間時，推進效率隨游速的增加而增大，其原因在于隨著尾鰭擺動速度的增加，推進力增加的速度大于側向力；當穩態游動速度在0.6Lm/s時推進效率達到最大，這是因為尾鰭推進力增加的速度和側向力相同；當游速大于0.6Lm/s后，推進效率隨著游速的繼續增大而逐漸下降，這是因為尾鰭的擺動幅值和頻率在不斷增大，側向力增加的速度超過推進力，消耗在水中的無用功也在持續增加。因此本文的研究對象游速在0.6Lm/s時推進效率最佳。

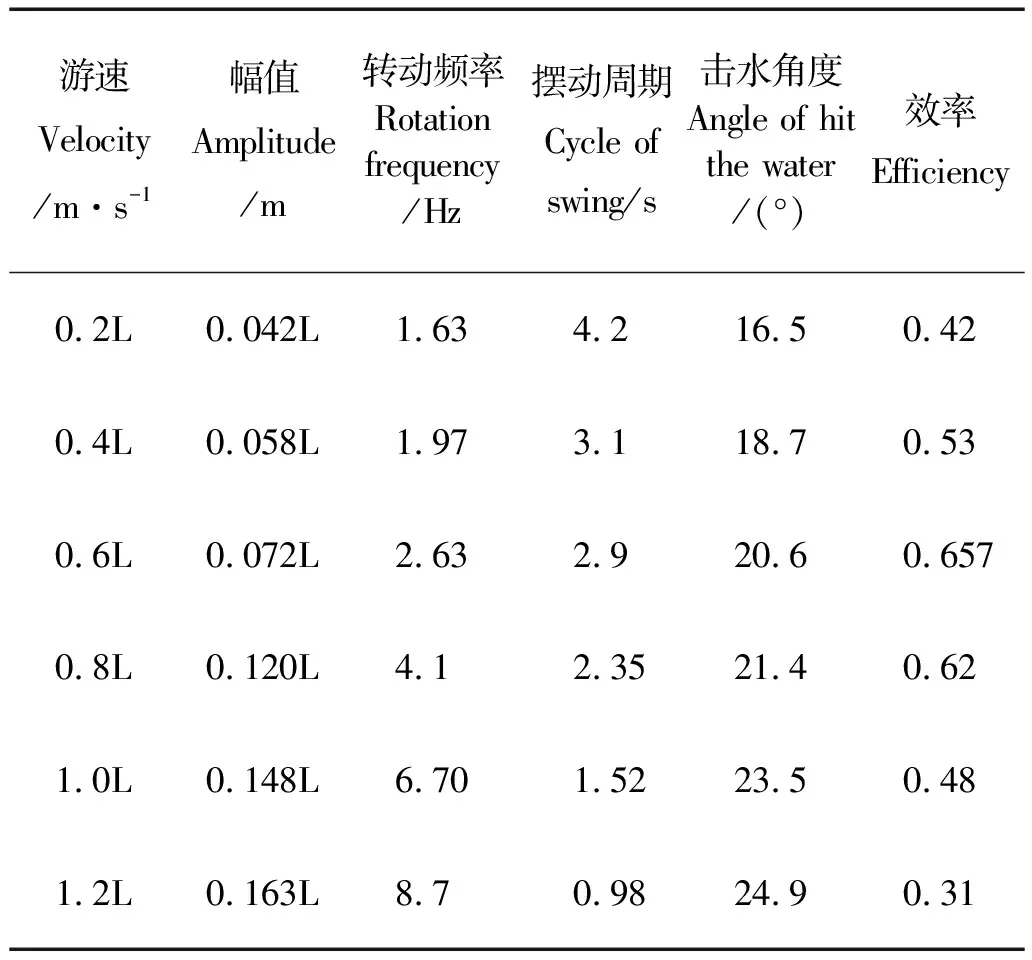
表1 參數優化結果

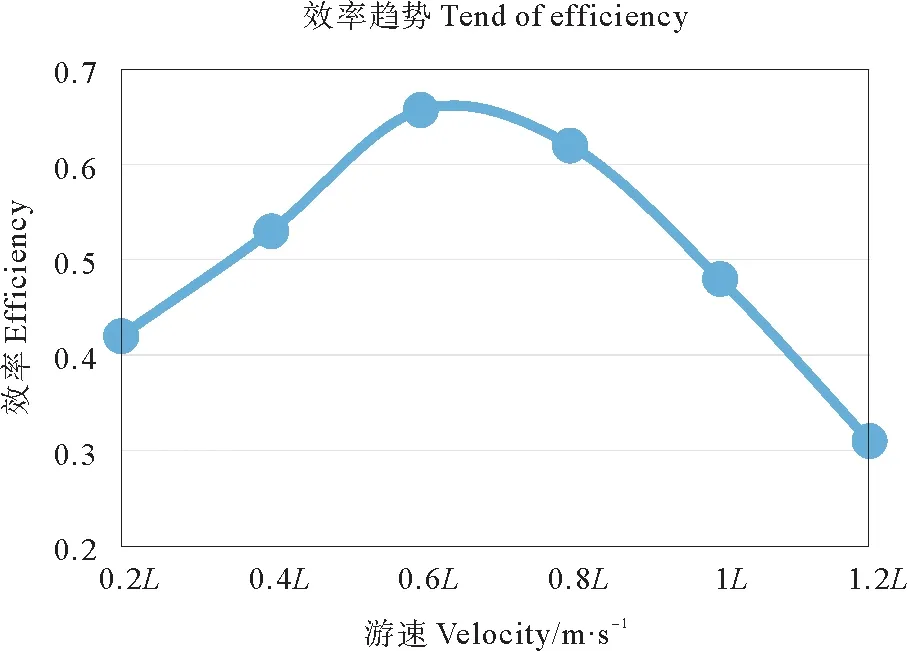
圖5 效率變化趨勢圖

轉動頻率趨勢和擺動幅值、周期趨勢分別如圖6、7所示，可以看出隨著游速的增大，尾鰭轉動頻率和擺動幅值都在單調遞增，角頻率是隨著游速的增大，增大的幅度在加快，而幅值增加的幅度在減緩，這說明增大轉動頻率和擺動幅值都能使游速加快，但由于體長的原因幅值不能無限增大，如果需要加速只能通過增大尾鰭轉動頻率的來達到目的。尾鰭的擺動周期變化趨勢如圖7所示，擺動周期隨著游速的增大而單調減小，是因為擺動頻率在增大，因此相應的周期也會減小。

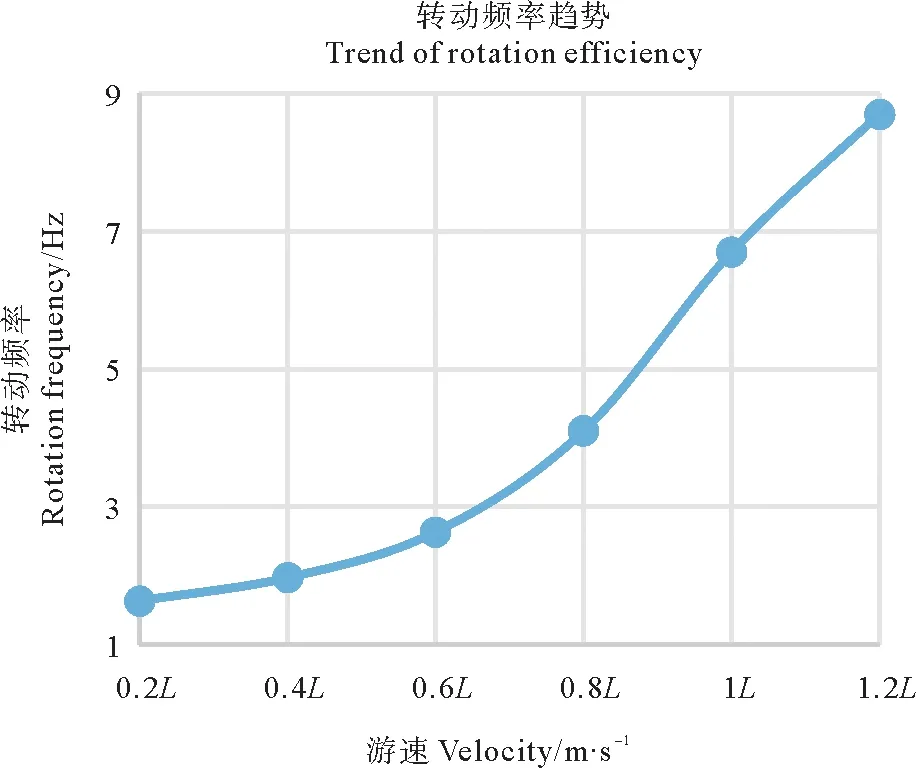
圖6 轉動頻率變化趨勢圖

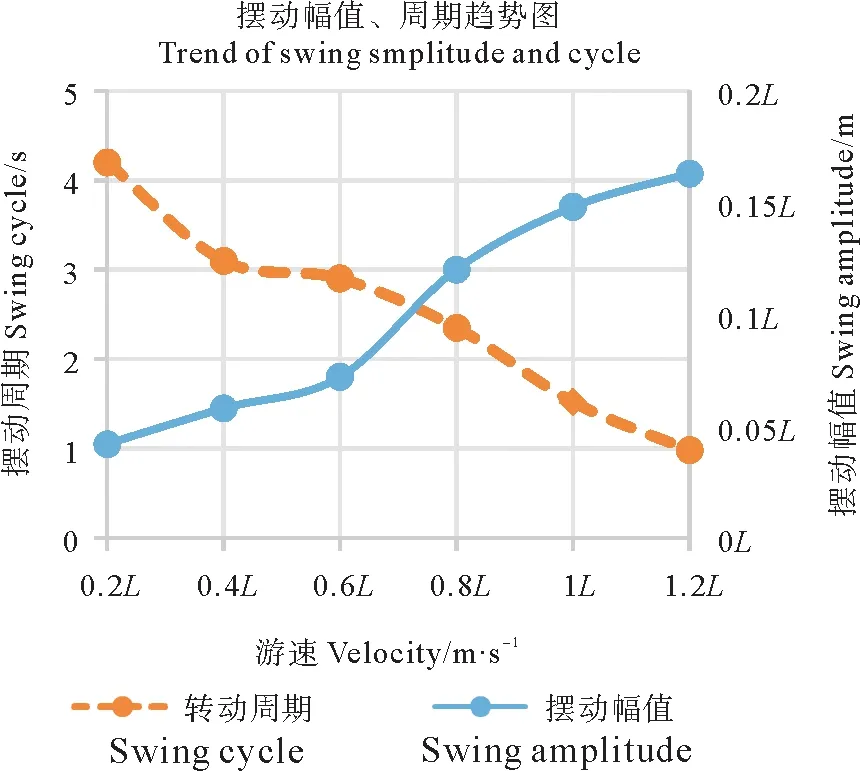
圖7 擺動幅值、周期變化趨勢圖

尾鰭的最大擊水角度變化趨勢如圖8所示，可知其隨著游速的增加而單調遞增，這說明當機器魚需要比較大的推進力時，尾鰭就會需要一個比較大的擊水角度來產生足夠的推進力，這個數據也吻合王冉冉[4]的研究成果。

3 仿真驗證

本文使用仿真軟件FLUENT進行仿真，并采用了動網格技術。仿真尾鰭在各游速下實際的推進效率，并與優化得到的推進效率相比較，來驗證上述算法是否正確。

圖9為本文采用的物理模型，圖10為本文仿真驗證所用的網格。

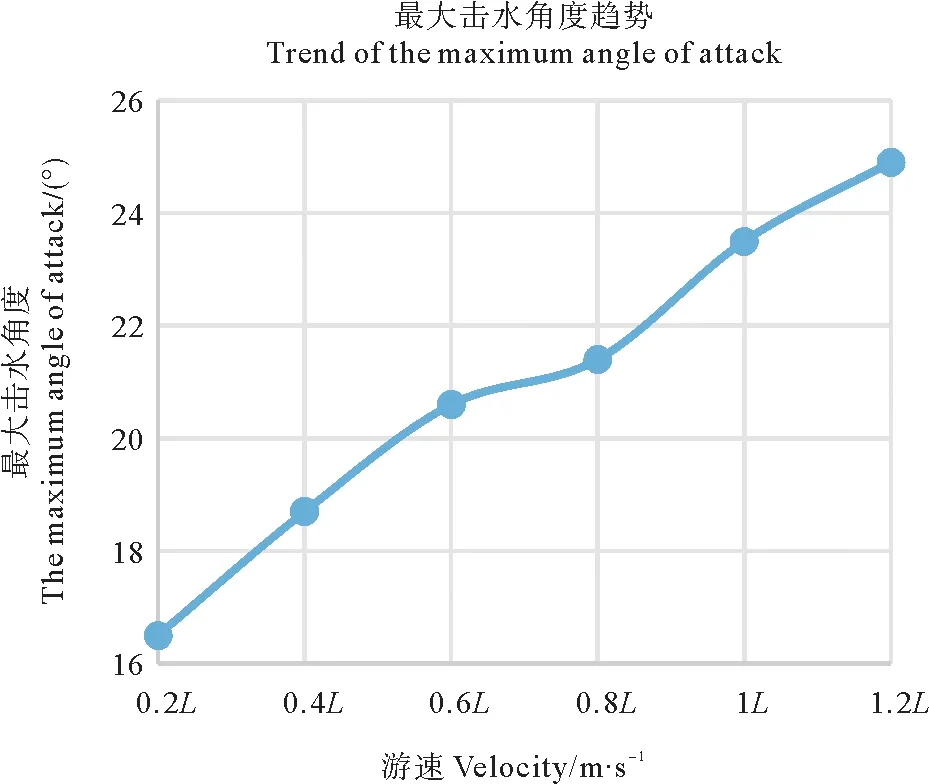
圖8 最大擊水角度變化趨勢圖

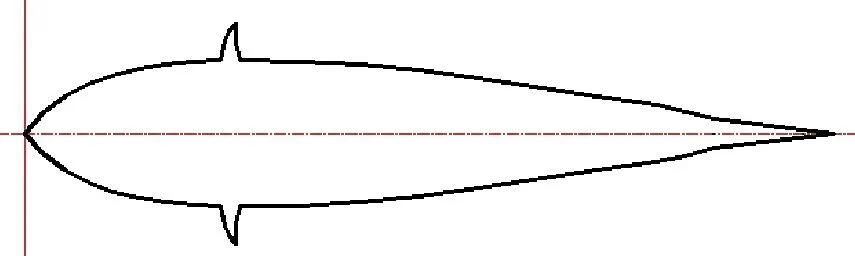
圖9 仿生機器魚的物理模型

圖10 仿生用網格

動網格仿真所需數據是各穩態游速下進行效率優化所計算出的結果，將這些數據加入到UDF中，就可以進行仿真。圖11為游速為0.6Lm/s時推進效率的仿真結果。

圖11 游速0.6Lm/s時仿真結果圖

圖中，(1 0 0)代表游動方向(x方向)上0.5個周期內產生的平均推進力FT，(0 1 0)代表水平面內游動垂直方向(y方向)上0.5個周期內產生的平均側向力FF。其推進效率為：

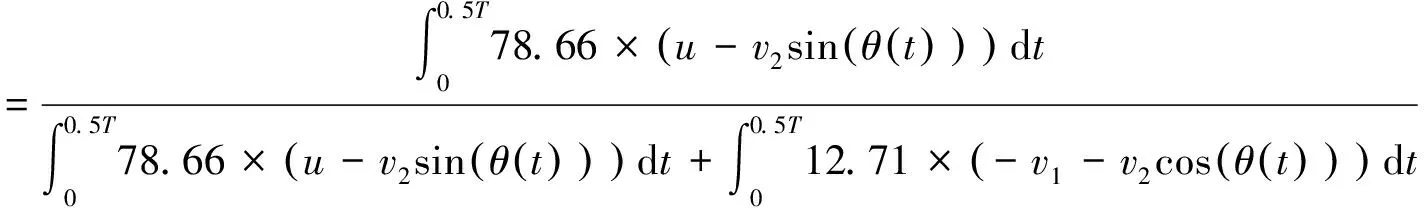
(6)

采用同樣的方法可得出其他游速時的效率，結果如表2所示。

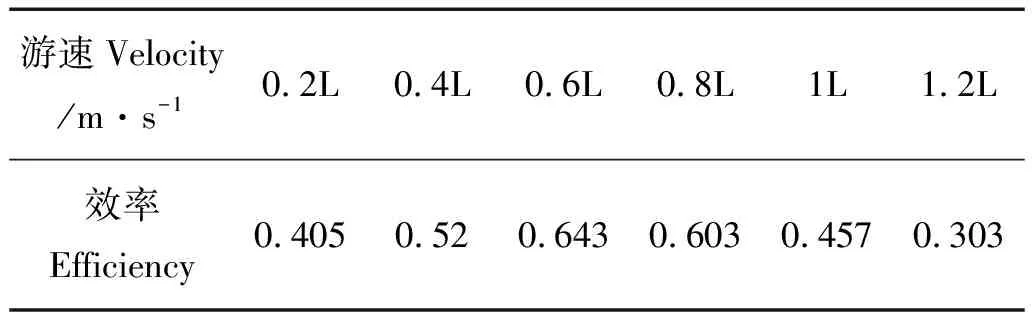
表2 仿真效率

圖12、13分別為游速0.6L和1.2Lm/s時的壓力云圖，可以看出游速為0.6Lm/s時尾鰭兩側受到的壓差大于游速為1.2Lm/s時的壓差，這說明游速0.6Lm/s時，尾鰭所受到的由壓差產生的推進力較大，這也從另一方面說明了為什么游速0.6Lm/s時的推進效率高于1.2Lm/s。

將數值計算的效率和仿真結果進行對比，如圖14所示，從圖中可以看出2種方法得到的結果變化趨勢是一致的，且數值接近，這說明本文所提出的數值計算方法是正確的。仿真所得效率值比數值計算結果稍低，這是因為仿真時流體粘性所產生的影響所致。

圖12 游速0.6Lm/s時壓力云圖

圖13 游速1.2Lm/s時壓力云圖

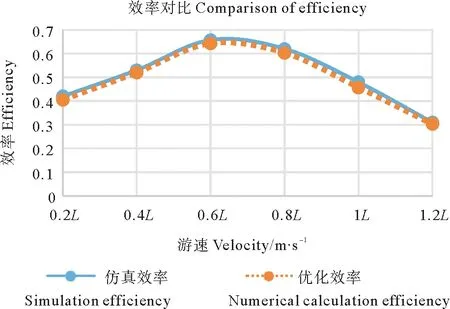
圖14 仿真結果與數值結算結果效率對比圖

陳宏在“仿生機器魚巡游和機動的運動機理研究”[5]中，得到的推進效率為0.58；陳斐[10]仿真了尾鰭的擺動幅值和擺動頻率等單一參數變化對推進效率的影響，得到的最高仿真推進效率是0.62。而本文的最高仿真推進效率達到了0.643，相較于其他的研究成果有了一定的提高，這主要是因為本文將尾鰭的轉動頻率、擺動幅值、最大擊水角度和擺動周期這4個參數進行了綜合優化，在游動過程中各參數之間密切協同，使尾鰭處于最佳工作姿態，從而提高了推進效率。

4 結語

本文根據仿生學的研究定義了尾鰭的4個游動參數，依據細長體理論建立了評價推進效率的數學公式，并進行了以推進效率為目標函數的多參數優化設計，采用遺傳算法對目標函數進行了多參數優化，通過FLUENT軟件對尾鰭的推進效率進行仿真，并將仿真結果與優化結果進行對比。

本研究得到的尾鰭最高仿真推進效率為0.643，最高數值計算推進效率為65.7%，通過對比目前的研究成果可以發現，尾鰭的多參數優化產生的效率高于單參數優化的效率，且存在不小的差距。因此，本研究所提出的尾鰭多參數優化方法是正確的。本研究針對研究目標得出的最佳巡航速度是0.6Lm/s，但是不同的游速都可以得出一組最佳的配合參數，這就為以后仿生機器魚的控制開辟了一種新的思路，在特定游速下首先優化出一組參數，通過這些參數的密切配合，達到在這種特定游速下效率最高的效果。