WSTi3515S阻燃鈦合金超塑性變形行為及本構關系研究

張學敏，曹宇霞，李 悅，焦奔奇,梁夢妍,袁戰偉,曾衛東

(1.長安大學,陜西 西安 710064)(2.西北工業大學 凝固技術國家重點實驗室,陜西 西安 710072)

0 引 言

為了防止發動機中鈦合金燃燒事故的發生，減輕飛機重量，滿足高推重比先進航空發動機的需要，各國競相開展了阻燃鈦合金的研制工作。2011年，西部超導材料科技股份有限公司聯合西北有色金屬研究院、北京航空材料研究院、西北工業大學等單位在美國研制的Alloy C(Ti-35V-15Cr)、Alloy C+(Ti-35V-15Cr-0.6Si-0.05C)和我國研制的Ti40(Ti-25V-15Cr-0.2Si) 合金的基礎上，通過調整V、Si、C元素含量，成功研制了一種新型高合金化β型阻燃鈦合金WSTi3515S合金(Ti-35V-15Cr-xSi-yC)[1]。目前已對該合金的熱物理性能、力學性能、熱暴露性能、工程化制備等方面進行了深入研究[2-5]，但有關其超塑性成形的研究尚未見報道。這可能是由于WSTi3515S阻燃鈦合金內部為單相粗大β晶粒，不能滿足細晶超塑性要求晶粒粒徑小于10 μm的前提條件。然而，近年研究表明具有粗大晶粒的鈦合金在適當的變形條件下也具有良好的超塑性[6-8]。大晶粒超塑性的實現對于縮短工藝流程，提高生產效率具有重要意義。鑒于此，研究了WSTi3515S阻燃鈦合金超塑性拉伸的力學行為，建立合金的超塑性本構方程，旨在探討WSTi3515S阻燃鈦合金的最佳超塑性變形條件，描述材料變形時熱力學參數之間的關系模型，為后續有限元數值模擬以及制定和優化成形工藝參數提供依據。

1 實 驗

實驗材料為熱軋退火態WSTi3515S合金，其原始組織為粗大的單相β晶粒，晶粒尺寸約為32 μm(圖1)。通過線切割將試樣加工成標距尺寸為10 mm×6 mm×2 mm的拉伸試樣，在試樣表面涂覆高溫抗氧化涂料。在大氣氣氛下，采用CMT4104型電子萬能實驗機進行等溫恒應變速率拉伸試驗，拉伸方向與軋制方向相同，試驗溫度范圍為800～920 ℃(溫度間隔為40 ℃)，應變速率為0.000 5、0.001、0.005、0.01 s-1。

圖1 熱軋退火態WSTi3515S合金的原始組織Fig.1 Original microstructure of roll-annealing WSTi3515S alloy

2 結果與分析

2.1 斷裂延伸率

圖2為WSTi3515S阻燃鈦合金板材在不同條件下拉伸后的延伸率。從圖2可以看出，應變速率較低時(0.000 5～0.001 s-1)，試樣的延伸率均達到300%以上，表現出良好的超塑性能，在變形條件為920 ℃、0.000 5 s-1時獲得最大延伸率556%。隨著應變速率增加，WSTi3515S合金的延伸率顯著減小，尤其在低溫(800 ℃)下，延伸率僅為186%左右。可見，WSTi3515S合金的大晶粒超塑性行為對于應變速率和溫度都非常敏感，但是仍具有相當寬的超塑性溫度范圍及應變速率區間。

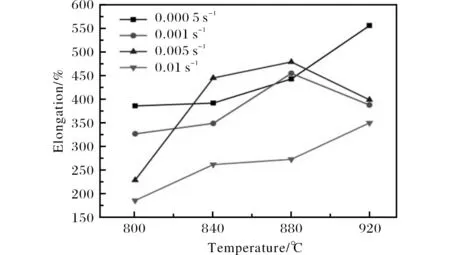
圖2 WSTi3515S合金延伸率隨溫度的變化曲線Fig.2 Curves of elongation various with temperature of WSTi3515S alloy

2.2 真應力-真應變曲線

WSTi3515S 合金超塑性拉伸變形的真應力-真應變曲線如圖3所示。從圖3可以看出，WSTi3515S合金在單軸拉伸過程中，穩態變形階段很短甚至不出現，變形主要集中在準穩態變形階段，且準穩態變形階段越長，獲得的延伸率越大。

準穩態變形區可以分為2個階段。第1階段為真應力逐漸升高的應變硬化階段。屈服之后，試樣在變形過程中表現出持續應變硬化行為，這種現象在Ti-6Al-4V合金的超塑性變形中也有發現[9-10]。研究認為，適當的硬化可有效抑制頸縮。硬化速率越慢，流動應力越穩定，越容易獲得高的延伸率。結合本研究中WSTi3515S合金的大晶粒特性，認為超塑性變形出現應變硬化的原因主要是由位錯塞積引起的。變形過程中只有處于有利取向的晶界才能產生滑移并參與合金變形，其余晶粒特別是大晶粒仍發生晶內滑移。晶內滑移造成位錯數量急劇上升，導致位錯塞積，引起應力上升。第2階段為真應力越過峰值后下降的應變軟化階段。超塑變形中產生應變軟化的原因主要有2個：①動態再結晶；②幾何頸縮。動態再結晶既可細化晶粒，又能引起應力松弛，使晶界滑移過程更容易進行，促使進一步變形所需的應力顯著降低。典型的動態再結晶現象已在粗晶Ti40阻燃鈦合金超塑性變形中觀察到，其真應力-應變曲線與WSTi3515S合金的變化趨勢類似[11]。幾何頸縮包括內頸縮和宏觀頸縮。變形時因內部空洞所占體積的增大和試樣變形不均勻性的增加，流變應力的計算值會降低。

圖3 WSTi3515S合金在不同應變速率下的真應力-真應變曲線Fig.3 True stress-strain curves of WSTi3515S alloy at different strain rates:(a)0.000 5 s-1；(b)0.001 s-1；(c)0.005 s-1；(d)0.01 s-1

2.3 應變速率敏感指數m值分析

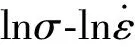
2.4 WSTi3515S阻燃鈦合金超塑性變形本構關系

WSTi3515S合金在超塑性變形時受到多種熱力參數的影響，可通過建立這些參數與材料流動應力之間的函數關系即本構方程來表征其超塑性行為。

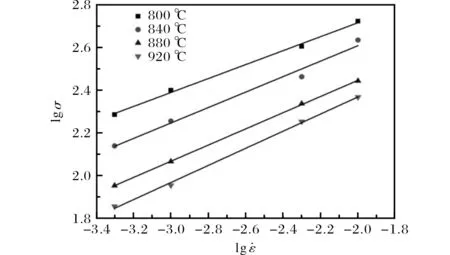
圖4 WSTi3515S合金的關系曲線 curves of WSTi3515S alloy

2.4.1 Arrhenius方程

超塑性變形過程屬于高溫變形范疇，也是一個熱激活過程，其變形溫度、應變速率對流變應力的影響可用Arrhenius方程表示[12]。

(1)

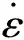
對方程(1)兩邊分別取自然對數，并設變形激活能Q與溫度T無關，整理可得：

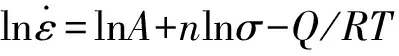
(2)

由方程(2)求偏導可得：

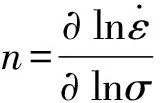
(3)

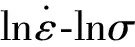
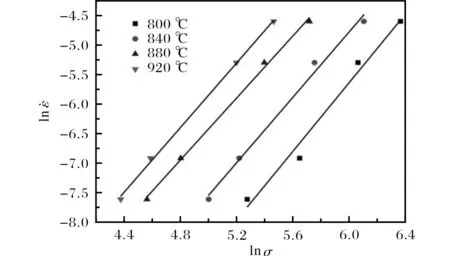
圖5 WSTi3515S 合金的關系曲線 curves of WSTi3515S alloy

由方程(2)可導出變形激活能的表達式為：

(4)

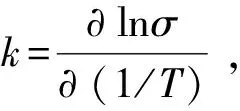
Q=Rnk

(5)

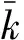
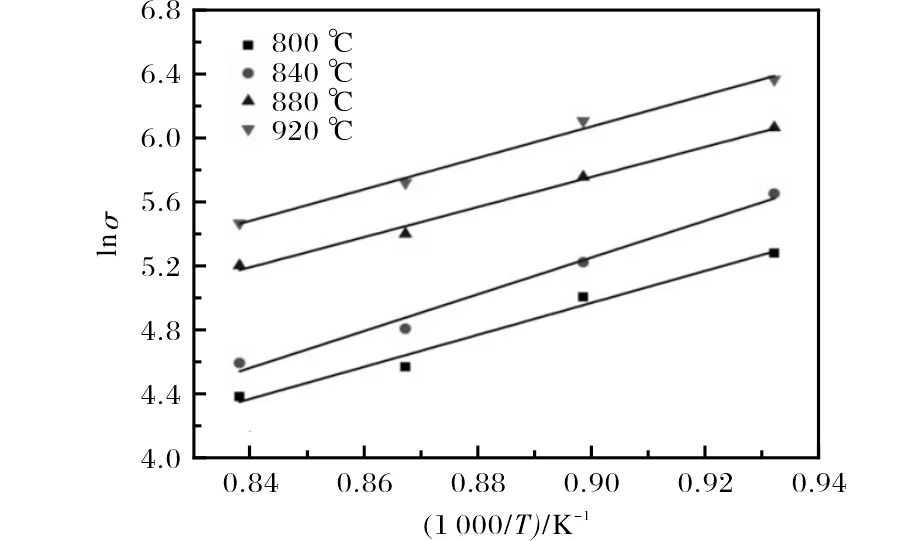
圖6 WSTi3515S合金的lnσ-1/T關系曲線Fig.6 lnσ-1/T curves of WSTi3515S alloy

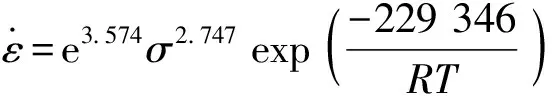
(6)

(7)

為了驗證所建立的本構方程的精確度，對不同溫度下的流動應力計算值與實驗值進行比較，結果如圖7所示。從圖7可以看出，所有數據點的相對誤差均小于15%，但部分數據點的相對誤差超過了10%，所構建的本構方程的精度并不高，因此需要通過更好的方式建立精度更高的本構模型。

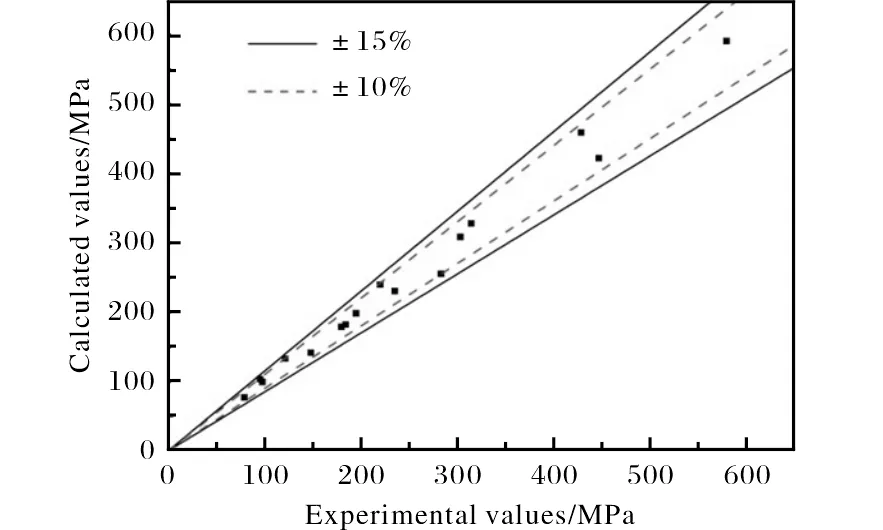
圖7 Arrhenius本構方程誤差精度效果圖Fig.7 Diagram of error precision of Arrhenius constitutive equation

2.4.2 多項式模型

多項式模型由于其計算精度高、擬合系數數量級相近等特點，已被廣泛應用于經濟、醫學、交通、工業控制等領域。常見的多項式模型包括溫度冪指數模型[13-14]、逐步回歸模型[15-16]和正交多項式模型[17]。本研究在逐步回歸模型基礎上，充分考慮應變、應變速率和溫度對流動應力的綜合影響，提出如下本構模型:

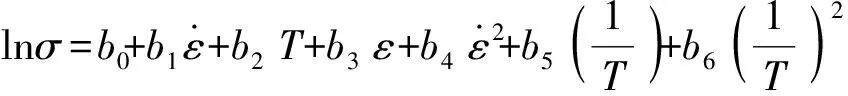
(8)

利用SPSS軟件對實驗數據進行多元線性回歸所獲得的回歸系數:b0=-8.046，b1=186，b2=0.006，b3=0，b4=-10 805.508，b5=0，b6=10 065 622.27，b7=27 872.619，b8=0.946，b9=-1 184.197，b10=35.738。

對多項式模型本構方程計算的流動應力值與實驗值進行比較，結果如圖8所示。由圖8可以看出，計數值與實驗值吻合程度較好，所有數據點的相對誤差均小于10%，相對誤差小于5%的數據點占總數據點的81.25%。因此，所構建本構方程的精度較高，能夠滿足數值模擬的精度要求。

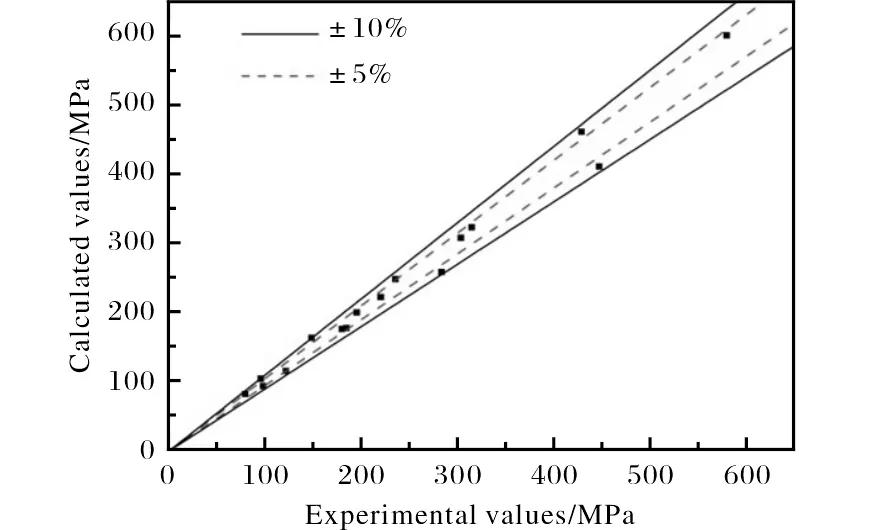
圖8 多項式模型本構方程誤差精度效果圖Fig.8 Diagram of error precision of polynomial model constitutive equation

3 結 論

(1) 原始晶粒粗大的WSTi3515S合金可在較寬的溫度范圍及應變速率區間內實現超塑性。合金在高溫低應變速率條件下具有良好的超塑性能，延伸率均在300%以上。最佳超塑性變形條件為920 ℃、0.000 5 s-1，該條件下獲得的最大延伸率為556%。

(2) WSTi3515S合金在超塑性拉伸過程中，穩態變形階段很短甚至不出現，變形主要集中在準穩態變形階段，且準穩態變形階段越長，獲得的延伸率越大。

(3) 采用Arrhenuis型方程建立的WSTi3515S合金超塑性本構關系精度不高；采用多項式模型構建的本構方程，相對誤差基本在5%以內，能夠滿足數值模擬的精度要求。