GPS電離層折射誤差的三階三頻改正模型及精度分析
陳少鑫,徐良驥
(安徽理工大學測繪學院,安徽 淮南 232001)
電離層折射誤差是GPS信號處理過程中的常見誤差之一,其主要的改正方法有:模型電離層誤差改正方法[1-3]、雙頻誤差改正方法[4-7]及GPS現代化后的三頻改正方法[8-9]。目前普遍采用GPS現代化后的二階三頻誤差改正方法削弱電離層對信號傳播的影響[10-12]。本文在GPS電離層折射誤差二階三頻改正方法的基礎上[13-14],提出了對電離層誤差進行三階改正的方法,并采用GPS三頻觀測數據進行試驗,驗證該模型精度的可靠性。
1 模型構建方法
1.1 電離層的折射誤差
GPS信號在電離層中傳播的單一頻率相位傳播折射率np與測距碼群波傳播折射率ng有如下關系
(1)
np=1-K1Nef-2±K2Ne(H0cosθ)f-3-K3Nef-4+…
(2)

(3)
式中,a1、a2、a3為簡寫后的系數。將式(3)代入式(1)得
(4)
當GPS信號穿過電離層時,由折射率變化引起的傳播路徑距離誤差及相位誤差為
(5)
將式(3)、式(4)代入式(5)得
(6)
(7)
1.2 電離層折射誤差三階三頻改正模型
在GPS三頻觀測數據中,L1=1 575.42 MHz,L2=1 227.60 MHz,L5=1 176.45 MHz,采用GPS三頻觀測數據,將電離層誤差改正至三階項。
由式(6)可得
(8)

其中,若令
由上式兩兩相減可得無電離層誤差的二階項組合為
則由上兩式相減可得無電離層折射誤差的三階項組合為
D5·(H2D3-H2D1-H1D3)·f21·σρp(f1)+
D3·(H1D5+H1D1-H2D5)·f22·σρp(f2)+
D1·(H2D5-H1D3)·f23·σρp(f3)=0
式中,若令W1=D5·(H2D3-H2D1-H1D3)·f21,W2=D3·(H1D5+H1D1-H2D5)·f22,W3=D1·(H2D5-H1D3)·f23,則可得
W1·σρp(f1)+W2·σρp(f2)+W3·σρp(f3)=0
(9)
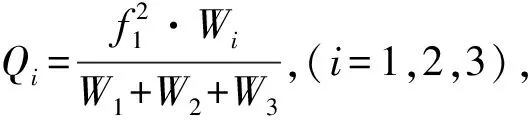
Q1·σρp(f1)+Q2·σρp(f2)+Q3·σρp(f3)=0
(10)

(11)
式(11)可消除電離層折射引起的一、二、三階誤差。若取ρ1、ρ2、ρ3分別表示f1、f2、f3的電磁波同步觀測所得觀測站至衛星的距離,消除電離層折射影響的路徑ρ0。則有
(12)
由式(12)得
式中,ρ12=ρ1-ρ2;ρ13=ρ1-ρ3;ρ23=ρ2-ρ3。
若令
由以上3式可得
(13)
由式(13)解得A1、A2、A3,并將其分別代入以下兩式
(14)
(15)
式(14)、式(15)分別為GPS三頻觀測數據相延遲、群延遲的三階改正。
1.3 電離層三階項折射誤差改正
由式(2)可得電磁波在電離層中折射誤差的三階項折射誤差為[8]
(16)

通過式(16)可求出電離層中的三階項折射誤差。
2 結果與分析
采用GPS三頻觀測數據[15]對電離層折射誤差改正方法進行了驗證。以2017年3月GPS三頻觀測數據為例,采用G17衛星、G05衛星、G09衛星的三頻觀測數據見表1。

表1 GPS三頻觀測數據
根據表1所示數據,電離層路徑延遲計算結果見表2。

表2 電離層路徑延遲分析

續表2
電離層路徑延遲改正結果見表3。GPS電離層折射誤差的三階三頻改正模型在路徑延遲改正中,相路徑延遲改正增大了約3.01×10-7m,而群路徑延遲改正減小了約3.45×10-7m。

表3 電離層路徑延遲改正差
GPS電離層三階項折射誤差計算結果見表4、表5。在GPS電離層折射誤差的二階三頻改正模型中,三階項折射誤差改正精度為58.3%;在GPS電離層折射誤差的三階三頻改正模型中,三階項折射誤差改正精度為98.8%。GPS電離層折射誤差的三階項折射誤差改正精度提高了40.5%。
表4TEC=1.38×1018、Nm=6×1012時電離層折射誤差的三階項改正
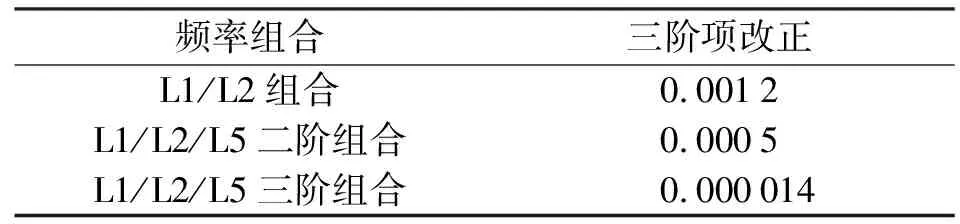
頻率組合三階項改正L1/L2組合0.0012L1/L2/L5二階組合0.0005L1/L2/L5三階組合0.000014
表5TEC=4.55×1018、Nm=20×1012時電離層折射誤差的三階項改正

頻率組合三階項改正L1/L2組合0.013L1/L2/L5二階組合0.0054L1/L2/L5三階組合0.00015
3 結 論
(1) 本文通過構建GPS電離層折射誤差的三階三頻改正模型,使電離層的三階項折射誤差改正精度從58.3%提高到98.8%,電離層折射誤差得到有效處理。
(2) 本文構建的三階三頻改正模型相比二階三頻改正模型,在電離層路徑延遲改正中,相延遲改正增大了約3.01×10-7m,而群延遲改正減小了約3.45×10-7m,使電離層折射引入的路徑延遲得到了控制。

