基于應用的《體育統計學》教學模式及相關問題思考

許 瑋

（南京郵電大學體育部，江蘇 南京 210071）

體育統計學是體育院系開設的一門主干課程。該課程要求學生具備一定的數理基礎，而體育專業的學生的數理基礎相對薄弱。因此，體育統計學的教學效果差和學生的定量思維能力難以培養的問題一直困擾著授課教師。筆者通過多年的體育統計學教學實踐發現，傳統教學模式不利于學生定量思維能力的培養，亟待通過創新體育統計學教學模式，改善體育統計學教學效果。傳統教學模式是一種“方法先入”的教學模式，即把統計學教學看成是方法學習的過程，從而過多地強調方法學習本身，而忽略方法背后的統計學本質——統計思想的教學。這種教學模式有三個弊端：一是方法的學習與方法的應用相割裂；二是讓學生誤認為為統計學習就是學習統計公式，統計應用就是應用統計軟件；三是易讓數理基礎差的學生產生厭學情緒。

本文通過案例分析和比較分析方法，闡釋“基于應用”的《體育統計學》教學模式的內涵、特征和優勢。以方差分析、因子分析為教學案例，剖析“基于應用”的統計學教學模式的基本原理，演示相應的教學過程，并針對該方法在實際教學運用中需要注意的幾個問題進行深入探討。

1 基于應用的《體育統計學》教學的模式內涵

基于應用的《體育統計學》教學模式，不能簡單地理解為“將統計學方法應用于實際問題”，而應該理解為“從應用的視角”去解讀“統計方法”，進而理解統計方法的確切涵義，從而達到培養學生定量思維的目的。

基于應用的《體育統計學》教學過程與解讀統計方法的形成過程相一致。遵循“提出問題-分析問題-解決問題”的邏輯路徑。統計學源于“解決問題”的需要而產生。因而，在課堂教學中應該充分重視面向“實際問題解決”的教學方法。換句話說，統計方法的產生源于“解決實際問題”需要，如果在學習方法的時候再回到“問題解決”這個起點上來，就很容易掌握統計方法的本質。它不僅可以避免陷入“死記公式”的陷阱，還可增加統計方法學習的趣味性。

下面我們以“單因素方差分析”為例來說明“基于應用”的體育統計學教學模式。為了考察單因素A的影響，分m個水平進行試驗，數據結構如表1所示。

表1 單因素方差分析數據結構

1.1 傳統教學模式下的方差分析教學過程單因素方差分析的關鍵在于理解離差平方和的關系。按照單因素方差分析理論可以將它們分為三個部分：總離差平方和，誤差項離差平方和以及水平項離差平方和[1]。在傳統的教學方法中，我們會推演總平方和是如何分解為誤差項平方和與水平項平方和的。總離差平方和,水平離差平方和。通過對SST式進行分解，得到兩個部分是SSA和SSE之和，從而有SST=SSA+SSE的結論。這樣的拆解公式會讓數理功底不好的初學者難以理解每部分的含義。

1.2 “基于應用”的教學模式下方差分析教學從應用角度看，方差分析的主要目的是比較多組均值是否相等的問題，對于例1中的數據，就是比較因素A的m個水平所產生的影響是否相同，而均值是否相等取決于變異部分。因此，方差分析最終又歸結到對變異進行分解的過程[2]。直觀上來看，上表數據變異主要來源于兩個部分，一是A因素引起的變異，二是隨機因素引起的變異（通常用字母E來表示）。這一區分直接引導我們對數據的變異進行分解。在分解變異之前，需要知道如何度量變異。在方差分析中，變異的度量主要是借助“離差平方和”來實現。接下來要做的工作是對各個部分的變異進行度量。總變異SST實際就是各個數據通總均值的比較而獲得，即。SSA可理解為消除掉個體隨機變異的影響后便是SSA。現在，我們假設沒有隨機部分的影響，即隨機變異為零，那么就有SSA=SST。具體而言，我們將每組數據均以各組的均值來代替，實際上就是消除了隨機部分的影響（見表2）,此時總變異為

表2 消除了隨機因素影響的數據結構

同樣的道理，我們假設因素A沒有影響，那么剩下的變異便是隨機變異SSE，數據結構見表3。此時，總變異部分。最后，我們通過表1-表3的對比發現，表2和表3的數據相合并正好等于表1的原始數據。這就間接地證明了SST=SSA+SSE。由此可見，基于應用的《體育統計學》教學模式的優點是直觀思維，避開公式推導，讓每一步分解都具有實際意義。即使是數理基礎不好的初學者，也能很快掌握方差分析方法的精髓。

表3 消除了A因素影響后的數據結構

2 “基于應用”的《體育統計學》教學中的幾點思考

基于應用的體育統計學教學實質就是從實際應用出發來闡釋統計學理論。讓學生們帶著實際問題來學習統計學，讓理論學習變得直觀而易于理解。在學生基本掌握了統計方法之后，我們再從傳統的理論教學進路來演示統計學方法，這一過程讓學生明白理論推導和應用之間的一致性，同時在統計理論上也有一個提高。前文的例子中，我們可以回到總離差平方和的代數式分解，代數式分解結果與我們“基于應用”視角進行的分析具有一致性。“基于應用”的統計學教學模式，雖然具有諸多優點，但在實際教學中，對于教師提出了更高的要求。

2.1 教師要透徹理解統計思想統計學的本質是方法背后的統計思想[3]。統計思想是為解決某一問題而提出來的思維方式，而此方法經理論化、模型化以后可以解決一大類問題。可以說，統計思想實際上是解決實際問題的一種思維方式的概念化（Generalize）。統計思想是統計方法的靈魂，如果抽掉統計思想這一內核，統計學只剩下公式的推演和證明，那么統計學就與數學沒有多大區別。

如果教師在課堂教學中不對統計思想講解透徹，就會給學生理解統計方法和學習統計原理帶來很大的困難。教師應該對一種方法的“統計思想”有深刻的理解，才能夠在教學中運用自如，而不至于在方法的“汪洋”中迷失方向，也只有如此，才能讓學生在統計學的課堂中抓住統計方法的靈魂。例如，在上述的方差分析中，理解了方差分析的“統計思想”就是“分解變異”時，就掌握了方差分析方法的精髓。適用于方差分析的實際問題可能千變萬化，但萬變不離其宗，只要我們牢牢掌握了該方法的統計思想，問題就可迎刃而解。

2.2 統計學教學中的“去數學化”前已述及，統計學的內核在統計思想，而統計學方法本身呈現給我們的是抽象的數學符號。面向數理功底較差的學生授課時，如何在講解中，將統計方法“去數學化”顯得很重要。所謂的“去數學化”實際就是將統計方法呈現給我們的抽象數學形式，轉換成我們易于理解的語言過程。“去數學化”也是對統計方法背后的統計思想的進一步細化和具體化。我們以因子分析為例來說明“去數學化”的重要性。

因子分析模型的解析表達式通常有如下的形式：假定P個隨機觀測向量，有均值，協方差，因子分析的模型可表達如下形式[4]：

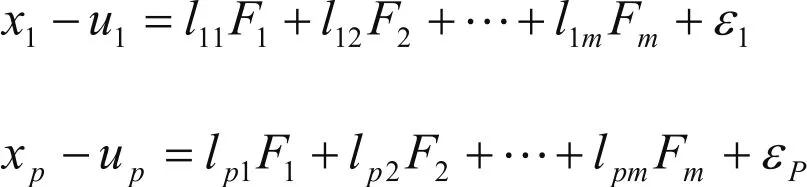
其中m個公共因子F1，F2…Fm和特殊因子，組成。若用矩陣表示，則是這一高度“數學化”的模型，往往讓文科學習者“如墜云霧”。

如何理解這一模型呢？我們在采用“基于應用”的統計學教學方法的時候，就需要對這一數學公式進行“口語化”轉譯。當然，轉譯的前提仍然是對因子分析統計思想有深刻的理解。因子分析模型的提出是基于這樣一種想法，即“希望用幾個潛在的，但不能觀測到的隨機變量去描述許多變量間的協方差關系”（這幾個潛在但不能觀測的隨機變量被稱為因子）。這里可以從兩個視角進行闡釋：一是從數據結構出發，我們可以認為因子分析要做的是通過線性變換，來重新表達數據結構，它希望變換后可以用少數因子來反映原數據的大部分信息。信息用什么來衡量？顯然就是這里的“協方差逼近”（Covariance Approximation）；也即是說如果數據線性變換后的數據協方差應該與原數據的協方差結構逼近。另一個視角是從數據相關性角度出發，我們可以認為因子分析是用變量間的相關性對數據進行重新分組，組內高度相關，而組間相關性較低。各組內變量象征有單一潛在的結構（因子）對觀察到的相關負責。前者更接近于數學表達式，后一種則更接近于實際應用。但無論是哪種視角去理解因子分析模型，最終都回到了“協方差逼近”上來。因子分析實質上也是一種統計變換，變換后的數據可以用少數因子來表達原數據結構的大部分信息。正是因為這一原因，很多教材也把因子分析看成是一種數據“降維”技術[5]。至此，我們基本理解了因子分析模型的數學表達式的含義,F代表“因子”，L代表“因子”的重要性程度（因子載荷）。

在課堂教學中，通過上述講解后，學生就會理解因子分析模型中每個符號都代表實際意義，因子分析的每一步分解也有相對應的價值。故而，在吃透統計思想的前提下實現將“用數學語言”表達的統計方法，轉換成我們能理解的表達方式（即去數學化），能取得更好的教學效果。

2.3 充分認識“統計距離”的重要性基于應用的《體育統計學》教學過程中，除了要充分理解方法本身所蘊含的統計思想外，還需要清楚具體統計方法是如何實現“統計思想”的。這就需要理解“統計距離”的概念及其表達的含義。它構成了“統計思想”與“統計方法”之間的橋梁。

“統計距離”與通常所用的“歐式距離”有相似的含義，都是度量兩點間差異性（或者數據的變異）。之所以提出“統計距離”的概念是因為有時候“歐式距離”并不能有效地度量兩點間的距離。例如在p維空間中的點在各個維度上“變差”（Variance）是不同，而“歐氏距離”未考慮這種變差的影響，而是將各個維度上的“重要性”等同看待。而“統計距離”在度量距離的時候，將各個維度上的“變差”考慮進去，從而能更準確地測度“數據變異”。

3 結 語

通過比較傳統教學方法與基于應用的統計學教學模式的優劣，可知傳統教學模式強調“方法先入”，其弊端是統計理論學習與統計應用相分離、學習統計原理變成了“死記公式”，甚至還會讓學生對體育統計學產生厭學心理。而基于應用為導向的教學模式，注重對統計方法背后統計思維過程的解析，從應用的視角，來解讀統計公式所表達的直觀含義，讓學生更快地掌握統計學方法的精髓。但基于應用的《體育統計學》教學對教師的要求更高，教師不僅要對統計理論和方法的本質做到了然于胸，善用“統計距離”鏈接“統計思想”與“具體統計方法”，搭建一座橋梁，幫助學生理解如何實現從“統計思想”構建“統計方法”。同時，在運用基于應用的《體育統計學》教學模式時，盡量做到“去數學化”處理。總之，基于應用的《體育統計學》教學模式教學效果的取得，很大程度上取決于老師對《體育統計學》中相關統計方法的理解和教學方法的靈活運用。