基于數據驅動方法的集裝箱龍門起重機能源系統健康狀態預測

杜明澤，嘉紅霞

(上海海事大學物流工程學院，上海 201306)

0 引 言

“油改電”后的集裝箱龍門起重機能源系統有3種形式：第一種是由市電供電驅動起重機主要工作機構及其輔助用電設備工作，小功率柴油機作為起重機轉場時脫離市電后的動力源；第二種是完全取消了柴油機，采用蓄電池作為起重機的動力源；第三種是串聯增程式可插電能源系統，也采用蓄電池作為起重機的動力源，但是需要小功率的柴油發電機隨時為蓄電池充電。后兩種方式都是全電驅的方式，尤其第三種方式是目前集裝箱龍門起重機“油改電”相關技術及應用研究的熱點方向。

可充電蓄電池組是全電驅集裝箱龍門起重機能源系統的主體部分。它既可以由市電或柴油發電機充電，又可以實時回收起重機起升機構下降時的勢能，實現起重機節能環保的目標。然而，相較于傳統的柴油機，蓄電池使用壽命較短，電池組整體更換價格也較高。因此，可以通過對能源系統中蓄電池健康狀態的實時評估，指導蓄電池的日常維護工作，及時更換單個電池，從而盡可能地延長電池組的壽命，減少電池組整體更換帶來的巨大花費，這是全電驅集裝箱龍門起重機能源系統研究中的關鍵問題。

目前，對可充電蓄電池健康狀態的預測主要有3種方法[1]：(1)基于物理模型的方法，即根據蓄電池的電化學反應原理建立電池等效電路模型進行預測，預測結果的精確度極大地依賴模型的準確性；(2)基于數據驅動的方法，即利用對電池性能的測試數據，利用各種分析學習方法從數據中挖掘出電池性能的變化規律，從而進行壽命預測[2]，如基于粒子群算法的自回歸模型[3]、高斯過程回歸模型[4]、基于粒子群算法的k最近鄰回歸模型[5]、樸素貝葉斯模型[6]等；(3)融合方法，即基于物理模型的方法與基于數據驅動的方法的聯合應用或多種基于數據驅動的方法的聯合應用以求獲得更精確的結果，如把人工神經網絡與卡爾曼濾波器聯合應用來預測電池的荷電狀態[7]等。

在現有的電池健康狀態預測研究中：針對鋰電池的研究較多，各類電池應用領域的研究者嘗試了多種基于數據驅動的方法，但目前并沒有形成有較廣泛應用的統一方法；針對鉛酸電池的研究較少，且大多采用了基于物理模型的方法，如Dirk Uwe Sauer 和 Heinz Wenzl采用物理化學老化模型(physico-chemical ageing model)、權重安時老化模型(weighted Ah ageing model)和事件導向型老化模型(event-oriented ageing model)預測鉛酸電池剩余壽命，并對3種模型的預測結果進行了分析[8]。然而，全電驅集裝箱龍門起重機能源系統屬于大功率能源系統，很難建立準確的電池模型，基于物理模型的預測結果精度較低。本文基于與現有集裝箱龍門起重機能源系統配套的能量監測管理軟件獲得的電池組工作數據，采用2種不同的基于數據驅動的方法對起重機能源系統中的蓄電池進行健康狀態預測，并將預測結果與實驗結果進行對比分析。

集裝箱龍門起重機能源系統中鉛酸電池的性能指標主要包括放電率、放電深度、工作電壓、電池內阻、電池容量、健康狀態等。一般地，電池的健康狀態以電池的容量損失為指標，電池的剩余容量越低，其健康狀態越差，隨著電池的不斷使用及老化，其容量會從最初的100%降至0[9]，因此電池的健康狀態可通過對電池在整個生命周期內剩余容量的預測進行評估[5]。本文即采用這種方法實現對集裝箱龍門起重機能源系統中鉛酸電池健康狀態的預測。值得注意的是，這里的電池剩余容量不是指電池單次使用過程中剩余電量的多少，而是指其充滿電后的實際容量，在電池的整個生命周期內，因老化或故障其實際容量總是會越來越小。當集裝箱龍門起重機能源系統實際容量過小，已經不足以驅動起重機各機構工作時，能源系統中的蓄電池就需要進行更換。

1 基于BP神經網絡的集裝箱龍門起重機能源系統健康狀態預測

神經網絡是由大量神經元廣泛互連而成的復雜網絡系統，能進行大規模并行信息處理，具有自適應性、自組織性和處理定量數據的能力，可以通過學習不斷適應環境，增加知識的容量。當前在神經網絡理論和應用方面已取得了豐碩的成果，本文采用BP神經網絡實現集裝箱龍門起重機能源系統健康狀態的預測。

1.1 BP神經網絡模型

采用典型的3層BP神經網絡結構，如圖1所示，包括輸入層、隱含層和輸出層，層與層之間采用全互連方式，同一層神經元之間不連接。

圖1 3層BP神經網絡結構

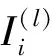
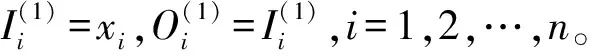
集裝箱龍門起重機能源系統中蓄電池的剩余容量與電池的諸多內部因素相關，其中最直觀的2個因素是電池的端電壓和內阻，在此將其作為電池剩余容量預測的輸入變量，即n=2。

(2)第2層為隱含層。該層用于實現輸入變量到輸出變量的映射，其節點數可在網絡學習過程中根據實際情況調整。隱含層采用Sigmoid函數作為變換函數。

設該層有q個節點，第j(j=1,2,…,q)個節點的輸入和輸出分別為

式中：wij為第1層第i個節點到第2層第j個節點的連接權值；θj為第j個節點的閾值；f(s)為Sigmoid函數，表達式為

f(s)=(1+e-λs)-1

(3)第3層為輸出層。該層仍然采用Sigmoid函數作為變換函數。第k(k=1,2,…,m)個節點的輸入和輸出分別為

式中：wjk和θk的含義分別類同于wij和θj。該預測模型的輸出變量為集裝箱龍門起重機能源系統中蓄電池的剩余容量，因此輸出節點只有1個，即m=1。

1.2 模型參數優化

利用優化算法中的梯度下降算法對BP神經網絡模型中的連接權值和閾值進行訓練，獲得優化值，使得預測模型的目標函數為最小值。目標函數取平方型誤差函數：

式中：yk,p為預測模型的輸出；Yk,p為期望輸出；N為網絡訓練樣本個數。梯度下降算法表示為

其中λ為訓練步長。

目前，典型的集裝箱龍門起重機能源系統一般采用DC 12 V、280 A·h的鉛酸電池。根據Kolmogorov定理和經驗，確定BP神經網絡隱含層的節點數為5。利用訓練樣本對BP神經網絡模型中的連接權值和閾值進行訓練，獲得優化的BP神經網絡模型。

2 基于最小二乘支持向量機的集裝箱龍門起重機能源系統健康狀態預測

支持向量機 (support vector machine,SVM) 是基于結構風險最小化原理的一種新型機器學習算法，它通過適當地選擇函數子集，可以根據有限樣本信息獲得較精確的解，在解決回歸問題上具有很好的應用。最小二乘支持向量機(least squares SVM,LSSVM)是SVM的一種重要改進，它采用最小二乘線性系統作為損失函數，將標準SVM的求解過程變成一個對等式方程組的求解，加快了求解速度，且所需樣本數更少。

2.1 LSSVM回歸模型

設樣本數據集{xi,yi}(i=1,2,…,N)，其中：xi為輸入向量，xi∈Rn；yi為輸出變量，yi∈R。LSSVM回歸模型[10]可以表示為

f(x)=wTφ(x)+b

式中：w=(w1,w2,…,wN)T為權值向量；b為偏置量；φ(x)為映射函數，它將輸入空間映射為高維空間。考慮函數的復雜度和對它進行擬合時得到的誤差，用一個優化問題來表示該回歸問題，其優化目標為

s.t.

yi=wTφ(xi)+b+ξi

式中：J是以w、ξ為自變量的優化函數；ξi是自定義的回歸誤差；γ>0是懲罰系數，用于調節誤差，γ值越大表示模型的回歸誤差越小。

引入Lagrange函數把上述帶約束的優化問題轉化為無約束的優化問題：

L(w,b,ξ,α)=J(w,ξ)-

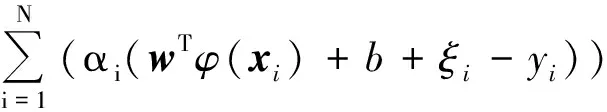
(1)

其中αi(i=1,2,…,N)是Lagrange乘子。

根據最優值條件對式(1)求偏導，并取核函數K(x,xi)=(φ(x),φ(xi))，可得

(2)

式中：I為N×N階單位矩陣；1=(1,1,…,1)為1×N階矩陣；y=(y1,y2,…,yN)T；α=(α1,α2,…,αN)T；Ω為方陣，由Mercer條件可知，存在映射φ(x)和核函數K(xi,xj)，使得

Ωij=φ(xi)Tφ(xj)=K(xi,xj),

i,j=1,2,…,N

由此，LSSVM模型又可以表達為

由式(2)可求得

采用徑向基函數作為核函數，即

式中：x是n維輸入向量；xi是第i個徑向基函數的中心；σ是標準化參數，也叫核寬度，體現了支持向量之間的相關程度，樣本輸入空間范圍越大σ取值也越大。

2.2 模型參數優化

以徑向基函數作為核函數，采用標準粒子群優化(standard particle swarm optimization,SPSO)算法對LSSVM 預測模型中的懲罰系數γ和核寬度σ進行優化，并最終計算出模型中的參數αi和b。

設在一個D維的搜索空間里有N個粒子，其中第i個粒子(i=1,2,…,N)的當前位置為Xi=(Xi1，Xi2，…,XiD)，當前速度為Vi=(Vi1，Vi2，…,ViD)。記第i個粒子搜索到的最優位置為Pi=(Pi1，Pi2，…,PiD)，整個粒子群搜索到的最優位置為Pg=(Pg1，Pg2，…,PgD)，則Pg稱為全局最優解。

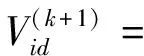
(3)

(4)

式(3)、(4)構成了基本粒子群優化(particle swarm optimization,PSO)算法，其中：d=1,2,…,D；k為當前迭代次數；學習因子c1和c2是為非負常數，一般在0～2范圍內取值，c1和c2分別調節粒子向自身最優位置和全局最優位置飛行的步長；r1和r2是區間[0，1]上的隨機數，且兩者之間相互獨立以保持群體的多樣性；為減小粒子在進化過程中離開搜索空間的可能性，Vid通常被限定于一定范圍內，即Vid∈[-Vmax，Vmax]，Vmax是由用戶設定的常數。

SPSO算法通過一個慣性權重ω來協調PSO算法的全局和局部尋優能力，即將式(3)修改為

這里，采用一種帶動量的非線性遞減權重方法獲得合適的ω：

式中：ωmax、ωmin分別為ω的最大、最小值，ωmax的典型取值范圍為0.9～1.4，ωmin的典型取值為0.4；kmax為最大迭代次數；2λ為動量，且λ=k/kmax。當k較小時，動量2λ接近1，ω接近ωmax，能保證算法的全局搜索能力；隨著k的增大，ω呈非線性遞減，保證了算法的局部搜索能力。當達到設定的最大迭代次數時，或粒子群搜索到的最優位置滿足設定的最小適應閾值時，迭代終止。

3 預測結果與實測結果對比

如前文所述，電池的端電壓和內阻為模型的輸入變量，電池的剩余容量為模型的輸出變量。模型的訓練樣本見表1。

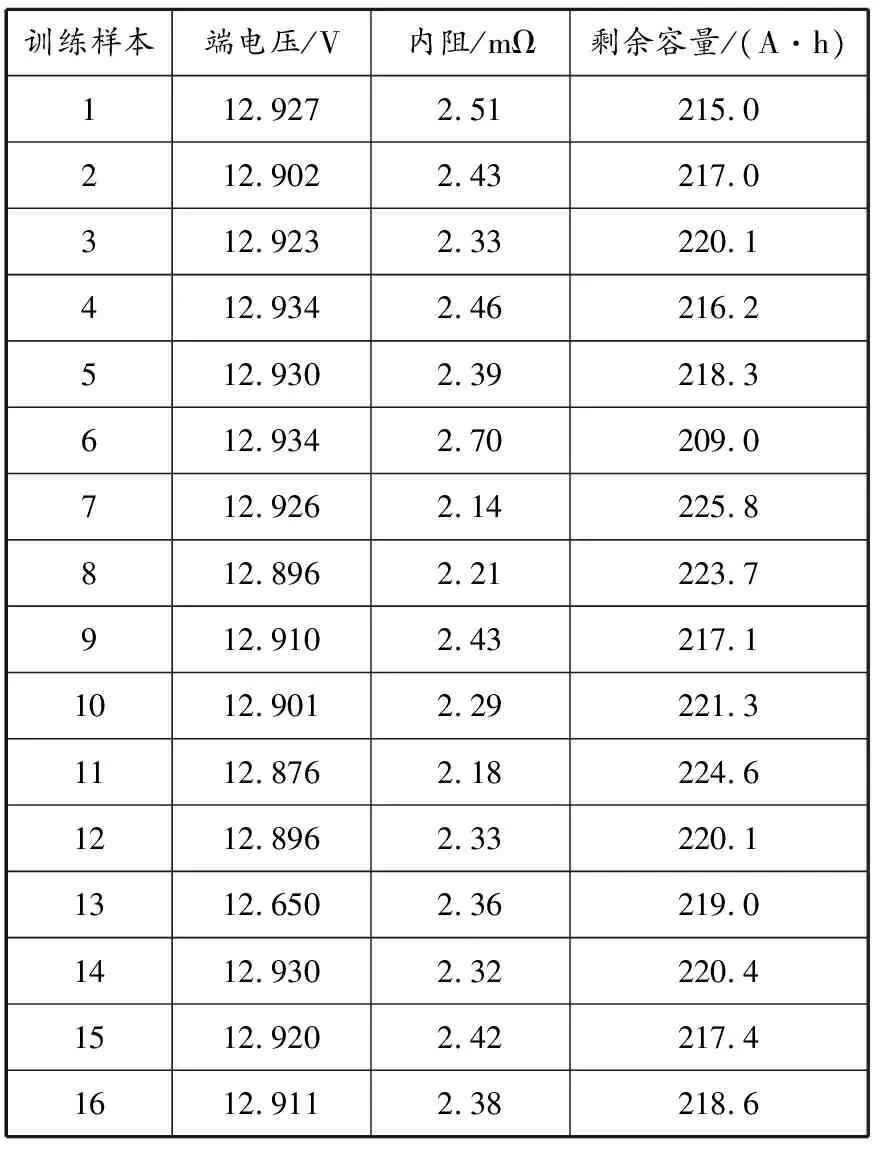
表1 訓練樣本

基于測試樣本，分別利用BP神經網絡模型和LSSVM模型對電池剩余容量進行預測。以起重機電池管理系統采集的電池實時數據為基準對預測結果進行評估，見表2。表2中的預測誤差采用的是相對誤差。

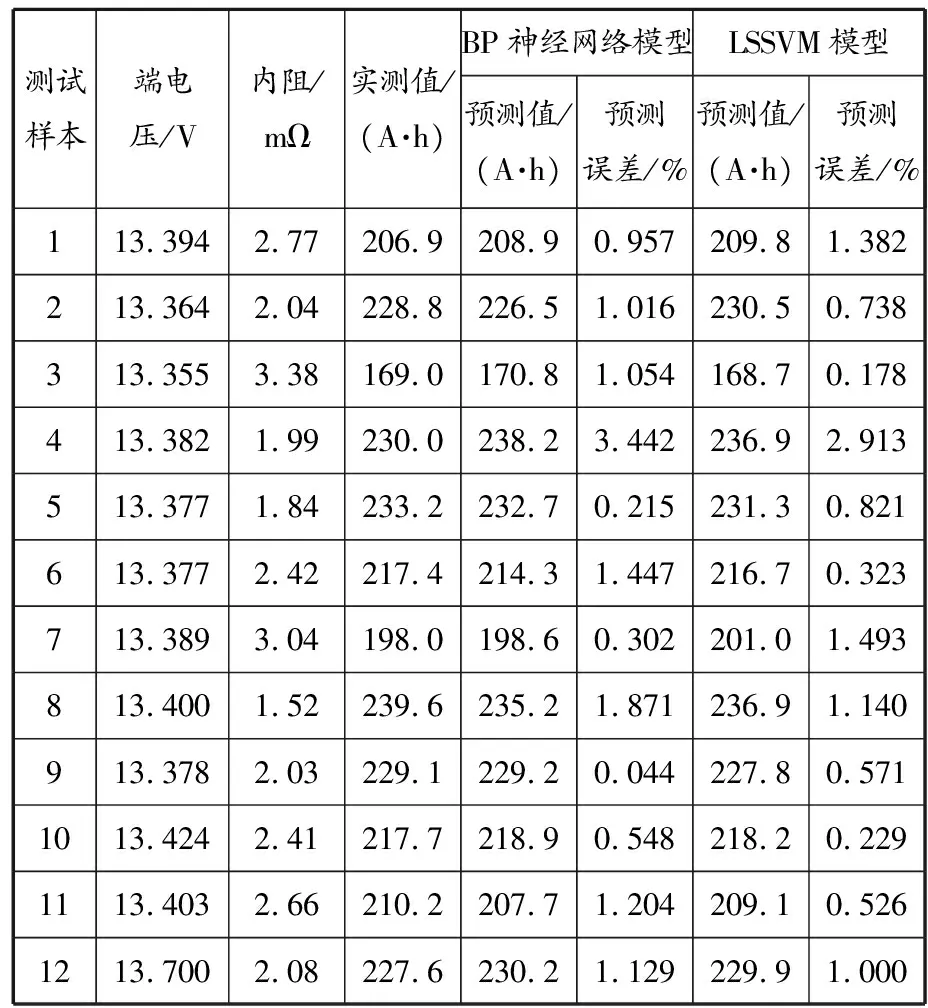
表2 電池剩余容量預測結果與實測結果對比

從表2可以看出：BP神經網絡模型和LSSVM模型對電池剩余容量的預測都具有高的精度，真實可信； LSSVM模型的預測精度高于BP神經網絡模型的預測精度，其原因既與兩種模型本身的特點有關又與集裝箱龍門起重機能源系統的工作特點有關。集裝箱龍門起重機的主要工作是利用其起升機構提升或放下貨物，能源系統在起升機構下降時吸收再生能源進行充電，在起升機構起升時作為起升動力源實現對外放電。因此，該能源系統在起重機進行裝箱工作時會頻繁充放電，電池完全放電間隔時間長，這就導致電池工作數據具有數據相似度高、樣本信息有限的特點。相較于BP神經網絡，SVM通過適當地選擇函數子集，更有能力利用有限樣本信息獲得較精確的解，因此其預測結果的相對誤差較小。

4 結 論

基于數據驅動的集裝箱龍門起重機能源系統健康狀態預測方法不需要建立蓄電池的物理模型，預測精度高。本文以電池在整個生命周期中的剩余容量作為電池健康狀態的評價指標，建立BP神經網絡模型和最小二乘支持向量機(LSSVM)模型；分別采用梯度下降算法和標準粒子群優化(SPSO)算法對模型參數進行優化；以電池端電壓和內阻兩個狀態值作為預測模型的輸入變量，提取集裝箱龍門起重機電池管理系統中的電池工作數據作為兩種預測模型的訓練樣本，獲得優化的模型后對測試電池樣本的剩余容量進行預測。

將兩種模型的預測值與實測值進行對比，結果表明，兩種模型的預測精度都較高，在實際應用中可以作為集裝箱龍門起重機能源系統日常維護保養、單個電池更換、系統整體評價、系統故障主動干預的依據。同時，對比結果也顯示LSSVM模型的預測精度高于BP神經網絡模型的預測精度，這主要是因為集裝箱龍門起重機能源系統具有頻繁充放電的特點，其工作數據重復度高、信息含量少，而LSSVM模型更適合處理具有這類特點的數據。