超高分子量聚乙烯平紋織物的穿刺沖擊模擬與響應分析

鄒畫眉 劉新金 謝春萍 蘇旭中 徐伯俊

摘要： 運用有限元方法對帶刃刀具刺穿超高分子量聚乙烯平紋織物的沖擊過程進行數值模擬，并通過準靜態實驗驗證有限元模型的有效性。通過給出布面刺破效果的數值仿真模擬，對織物刺穿過程中的紗線的應力應變分布進行分析，得到沖擊系統的能量變化規律。數值模擬結果指出：刀刺織物過程中，刀具的能量主要轉化為織物的彈性應變能，其余為塑性耗散能和摩擦耗散能;紗線破壞以剪切斷裂為主;平紋織物的彈性回復性能有助于抵抗刀具的沖擊，增強其抗剪切性能是提高防刺性能的關鍵。

關鍵詞： 有限元;平紋織物;穿刺;準靜態實驗;能量

中圖分類號： TS101.923 ? 文獻標志碼： A ? 文章編號： 1001-7003（2019）06-0046-06 ? ?引用頁碼： 061108

Abstract： The impact process of the edged cutter piercing UHMWPE plain weave fabric was numerically simulated by finite element method， and its effectiveness was verified by the quasi-static experiment. The numerical simulation of cloth surface piercing effect was given to analyze stress and strain distribution of yarns in the piercing process， and the energy change law of impact system was gained. The numerical simulation results show that the energy of the cutter is mainly converted into elastic strain energy of fabric in the fabric piercing process， while the rest is plastic dissipation energy and friction dissipation energy. The failure of yarns is mainly due to shear fracture. The elastic recovery property of plain fabric is helpful to resist the impact of cutter. Enhancing shear resistance of the plain fabric is the key to improve its stab-proof performance.

Key words： finite element; plain weave; puncture; quasi-static experiment; energy

柔性織物和紡織結構復合材料因其質輕柔軟、高強耐沖擊的特點被廣泛運用在特種防護織物，如擊劍服、防刺防彈服的研發上[1-2]，其中最典型的代表就是纖維增強復合材料。而纖維增強體在纖維增強復合材料中提供材料的強度和剛度，起主要作用[3-4]，因此，對于增強體的力學研究和抗沖擊性能預測頗為重要。利用有限元模擬計算纖維增強體在沖擊下的力學響應，一方面避免了制作大量的試樣，降低了生產成本;另一方面能夠更細致深入地分析紡織結構的力學響應，這是單純進行力學實驗所不能達到的，因而成為了當下的研究熱點。

有限元分析包括建模、材料屬性賦予、建立分析步、設置相互作用、劃分網格、施加載荷與邊界條件、提交任務與可視化分析等步驟[5]。本文利用有限元軟件Abaqus模擬分析了帶刃刀具穿刺平紋織物的靜態力學響應與動態力學響應，探尋穿刺的基本機制，以期對平紋織物防刺性能的提高提出建設性的思路。刀具穿刺織物過程含有大變形和復雜的接觸關系，是高度非線性問題，采用隱式動力學（Standard）分析很難收斂，因此用顯示動力學方法（Explicit）進行分析。實際生活中，人持刀具穿刺織物過程中，刀具的速度不僅受織物的反作用，還受變化的外力或重力操控，但是在使用計算機進行動態穿刺模擬時，忽略人力，給刀具一個初始速度，只考慮織物與刀具間的相互作用，簡化研究過程，探尋沖擊響應基本規律，為防刺材料的復合結構設計與力學性能預測奠定理論基礎。

1 沖擊系統建模與前處理

整個穿刺沖擊系統包括織物與刀具兩部分。平紋組織是最基本的二維機織物結構，因為它在二維機織物中最為緊密堅牢，所以應用最為廣泛。超高分子量聚乙烯（Ultra-high molecular weight polyethylene， UHMWPE）是目前抗沖擊性能最高[6]的高性能材料之一，因此，本文選用一種超高分子量聚乙烯平紋織物材料進行仿真模擬，刀具選用參考GA 68—2008《警用防刺服》。

UHMWPE纖維的力學性能具有應變率敏感性，即在不同的應變速率下，其應力應變曲線不同。特別在高應變率（102～104s-1）與超高應變率（104～106s-1）下，UHMWPE材料會有明顯的模量增加、最大應力增大與失效應變減小現象。而本文所研究的刀具穿刺織物過程為低速沖擊，屬于中應變率實驗。如GA68—2008《警用防刺服》中對防刺性能測試的規定：讓質量為2.4kg的刀具自由落體以（24±0.5）J的撞擊能量刺入織物并檢查織物能否穿透。經計算，標準中刀具接觸織物時的速度約為4.47m/s，而實際生活中，手持刀具穿刺織物的速度不超過10m/s，穿刺過程中纖維紗線的應變率小于102s-1，纖維紗線的力學性能與靜態等速拉伸試驗（應變率約為10-2s-1）時的力學性能差異不明顯。且本文的動態穿刺模擬只作為探討穿刺機制的研究手段，不作為實際材料防刺性能預測的依據。因此，有限元模型中暫且忽略了UHMWPE的應變率效應，假設紗線在動態穿刺過程中的應力應變曲線與靜態拉伸實驗所測得的參數一致。

1.1 建 模

1.1.1 織 物

平紋織物試樣的組織結構參數通過超景深三維顯微鏡拍照測量取得，如表1所示。用各種CAD軟件建模再將模型導入有限元軟件，存在計算速度慢與信息易丟失的缺點，因此，建模操作在有限元軟件Abaqus自身的Sketch模塊進行，按照實際織物試樣的結構參數1 ︰ 1畫出紗線，建立8cm×8cm大小的織物模型。因實際織物中紗線相互交織，交織點處紗線相互壓扁，因此假設紗線截面為橢圓形，這樣亦不易造成紗線間的過盈接觸。將橢圓截面沿著樣條曲線掃掠便可得到一根紗線的模型。將一根紗線通過陣列和三維旋轉等操作，畫出平紋織物的模型（圖1）。

1.1.2 刀 具

不同刀具的穿刺機制不同[7]。美國NIJ 0115.00《個體防刺衣》標準中，將刀具分為有刃刀具和錐形刀具，有刃刀具又分為單側刃和雙側刃刀具。錐形刀具沖擊織物過程中不含有剪切作用，只有拉伸斷裂破壞;一般刀具都為帶刃刀具，穿刺織物的過程中既有剪切破壞，又有拉伸破壞。中國公安部GA68—2008《警用防刺服》標準中的規定實驗刀具即為一種單側帶刃刀具，具有典型代表性。

按照GA68—2008《警用防刺服》中標準刀具的參數繪制刀具模型。考慮到刀具剛度非常大，穿刺過程中幾乎不會形變，也無需考察其應力分布，因而將刀具定義為離散剛體，不需賦予材料屬性，只需定義參考點。為了減少單元數量、加快計算速度，只畫出其刀尖部分。

1.2 前處理

1.2.1 賦予材料屬性

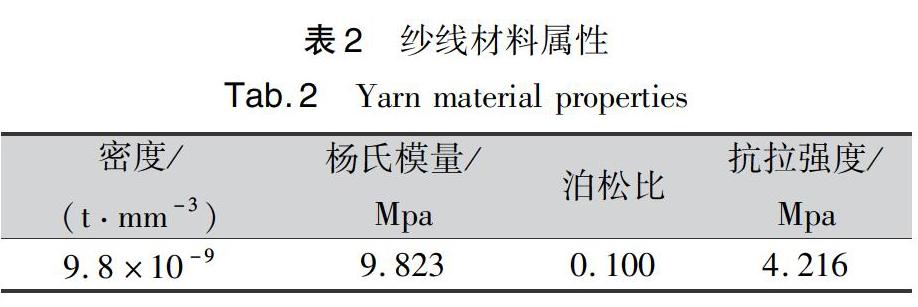
本文模擬的二維織物選用高性能纖維——超高分子量聚乙烯（UHMWPE）作為材料，拆取試樣織物的多根UHMWPE紗線進行拉伸斷裂等實驗，得到紗線的彈塑性等屬性參數如表2所示。在Property模塊中輸入屬性參數，定義失效準則，并設置與位移相關的損傷演化。

1.2.2 劃分網格

用剛性單元劃分離散剛體，刀具共劃分為了2093個R3D4單元;用減縮積分單元劃分實體，紗線共劃為17600個C3D8R單元，同時增加一個人工的沙漏剛度以防止出現沙漏現象。

1.2.3 其他前處理

將刀具與織物裝配好（圖2），刀尖與織物表面接觸，首先給刀具的參考點施加一個10000mm/s的恒定速度約束，給織物四周的紗線端施加PINNED約束（位移為0），紗線間、紗線與刀具間的摩擦系數設為0.1，建立顯示動態分析步，提交計算任務，得到靜態穿刺數值模擬結果。

2 準靜態實驗驗證

2.1 實驗過程

利用萬能試驗機對UHMWPE平紋織物試樣進行準靜態刺破實驗（圖3），刺破過程盡量均勻緩慢，以保證各時刻沖擊系統的狀態接近平衡態。用自制的正方形夾具夾住布樣，實驗前將刀頭下降到與布樣表面剛好接觸，布樣有效受力范圍為8mm×8mm，設置實驗過程中刀具下降速度為10mm/min后開始實驗。

需要說明的是，在Abaqus軟件中用顯示動力學方法（Explicit）模擬準靜態問題時，穩定時間增量很小，以自然周期（10mm/min×1.3min）計算將耗費相當長的時間，是不切實際的。因而為提高計算效率，需要人為地提高刀具設定速度，將時間長度控制在0.01s以下。在有限元中嘗試了2000～12000mm/s的不同刀具速度設置，發現：速度為2000～6000mm/s時，計算效率很低;速度大于11000mm/s時，偽應變能很大，織物動能/內能的比值過大，計算中斷，結果失真;速度為7000～10000mm/s時，計算效率較高，且不同速度的數值模擬結果具有一致性，具有參考價值。因此，將有限元中刀具速度設置為10000mm/s。

2.2 實驗結果

將Abaqus數值模擬結果與刺破實驗結果相比較，可以發現：兩者沖擊后的布面形態高度相似，紗線轉曲滑移的位置形態及破口的大小基本一致（圖4），實驗布樣的破口略小，可能是由實驗結束后刀具抽出布樣稍有回復導致的。對比兩者刀具的頂破力-位移曲線（圖5）亦可發現一致性。兩條曲線的走向基本吻合，在7mm和11mm左右均有明顯的頂破力下降和震蕩，分析認為是由于紗線的失效斷裂導致，而模擬的結果比實驗結果略有延遲，但亦在誤差允許范圍內。由此可以驗證：織物的建模方式有效，有限元中紗線的屬性參數設置相對準確，刀具速度的數量級提高沒有使結果退化失真，在可接受的范圍內。

3 沖擊響應分析

為探尋布面受到刀具沖擊后響應的基本規律，決定給刀具一個初始速度，只考慮織物與刀具間的相互作用，不考慮外力做功，從而簡化研究過程。在Abaqus軟件中可以實現這種理想狀態。實際織物織制得非常緊密，且紗線無捻，導致紗線扁平，寬高比很大，截面某些地方曲率過高，不利于網格的劃分。因此在Abaqus中用同樣的建模方式建立一個經緯密較小、紗線更圓的織物模型，紗線屬性設置及其他前處理方式與上文相同。假定刀具與織物接觸時的速度為8m/s，設置模型中刀具的初始速度為8000mm/s，提交計算任務，分析動態穿刺數值模擬的結果。

3.1 刺穿過程

圖6顯示了刀具刺穿織物而后被彈回的過程中織物的應力變化與變形情況。由此動態云圖可以看到：0～0.0045s，刀具漸漸刺入織物，紗線受到擠壓拉伸，布面漸漸突起;0.0045s時，織物凸起最為明顯，紗線開始斷裂;到0.005s刀具刺穿平紋織物、其中一根紗線完全斷裂后，織物顯現出一個收緊的趨勢，刀具不再刺深并向相反方向移動;直到0.0075s時，織物繼續收緊回復，刀具又后退了一些距離。結合刀具的速度曲線、位移曲線（圖7），可以總結出整個刺穿過程分為刀具刺入與被彈回兩個階段。

3.2 織物的應力應變分布

從圖6中的應力分布可以看出，刀尖從紗線空隙中刺入，紗線受到擠壓拉伸，應力逐漸提高。主要體現在隨著刀具的深入，與刀具接觸部分紗線變形增加，應力持續增大，紗線與紗線交織點處的應力也逐漸增加，同時，織物四周的固定端出現應力集中。而刀尖四周部分紗線應力最大，這是因為此處所受的拉伸力與剪切力最大。通過查詢節點力值，發現紗線斷裂前的拉伸應力遠未達到抗拉強力，由此判斷紗線是因剪切斷裂。當與刀刃接觸的紗線受到剪切力而斷裂失效后，斷裂紗線的應力驟減（圖8（a）），與這根紗線交織的紗線上的交織點的擠壓也立即減小，應力大幅下降（圖8（b））。周圍的紗線趨于伸直，布面趨于收緊回復，布面的平均應力水平下降，應變的分布變化與應力同步為正相關。

3.3 沖擊系統的能量變化

有限元力學分析中，能量守恒遵循熱力學第一定律，整體模型的能量平衡可以表述為：ETOTAL=ALLIE+ALLKE+ALLVD+ALLFD-ALLWK=constant[8]，即：總能量=內能+動能+粘性耗散能+摩擦耗散能-外力功=常量。本模型的這幾種能量關系如圖9所示。

沖擊系統內外力做功為零，系統動能主要是由刀具貢獻，且不考慮黏性耗散。由計算完成后的能量歷程輸出圖可以看出，模型的總能量守恒，證明了模擬結果的準確性。正向穿刺過程中刀具的動能被織物吸收，且大部分轉化成了織物內能，還有一部分能量由于紗線之間、紗線與刀具間的摩擦作用耗散。刀具反向移動時，織物的內能又轉化為刀具的動能，刀具反向速度增加。

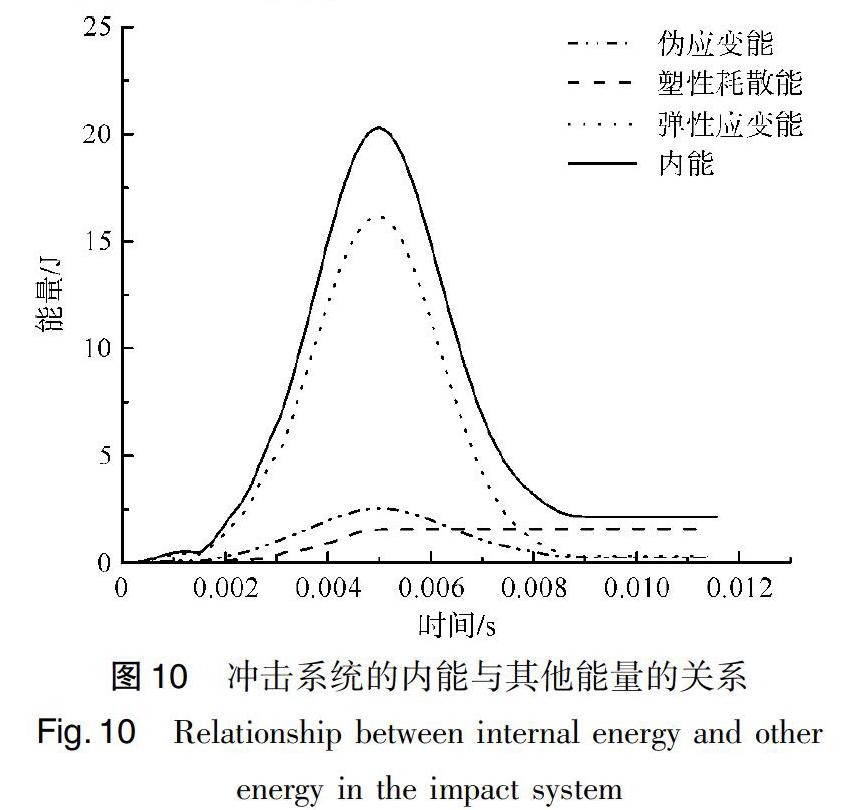
整體模型的內能遵循下式：ALLIE=ALLSE+ALLPD+ALLCD+ALLAE[8]，即：內能=彈性應變能+塑性耗散能+蠕變耗能+偽應變能。這幾種能量的關系如圖10所示。

由圖10可見，彈性形變產生的彈性應變能占了內能的大部分。刀刺織物時，刀具的速度逐漸減小，起初是由于刀具擠壓織物導致紗線拉伸產生彈性形變，吸收了刀具大部分的能量，并轉化為織物內能，而后某些紗線開始屈服，塑性變形直至失效斷裂，這部分的蠕變耗散能與塑性耗散能占比很小。進一步說明刀刺織物時，紗線因拉伸塑性變形斷裂的情況很少，主要是受剪切而斷裂。也就是說：大部分紗線強度在未達到其抗拉強度時，已經受到剪切作用而破壞。

經計算，圖10中偽應變能/內能<10%，根據相關有限元理論[8]，說明控制沙漏變形所消耗的應變能在可接受的范圍內，模擬的結果具有可參考性。

4 提高防刺性能的措施

根據有限元軟件的模擬結果，可以看出帶刃刀具沖擊刺破平紋織物的過程包含了頂穿和切割兩個方面。要想得到良好的防刺效果，織物必須具有優異的抗剪切和抗拉伸性能，其中抗剪切性能占首要地位。

4.1 提高抗拉伸性能

穿刺過程中，刀具的能量主要轉化為紗線形變能（主要是彈性應變能）和摩擦耗散能。因此，優先選用屈服強度極高的纖維紗線，延長布面通過自身彈性形變對刀具能量的吸收的時間;其次，紗線的抗拉強度也盡量要求高。在一定范圍內增加紗線表面摩擦因數，從而增加紗線間、紗線與刀具間的摩擦力，可以吸收更多的能量，但是這一部分占比較小，對防刺性能的影響不大，這與文獻[9]的實驗結果相符。

4.2 提高抗剪切性能

平紋織物紗線的剪切模量、細度、經緯密、組織結構等對其抗剪切性能影響較大，可采用單因素實驗與正交實驗進一步探尋這些因素的影響。平紋織物的防刺優勢在于其良好的彈性回復性能，但是由于紗線間只是簡單交織，沒有黏結，單根紗線很容易被割斷，因此其抗剪切性能不如無紡布，可考慮將機織布與無紡布疊層復合，以發揮兩者的優勢;或者將平紋基布進行樹脂涂層處理[10]，增強織物的防刺性能。

5 結 論

通過準靜態穿刺實驗，驗證了運用有限元方法模擬計算刀具刺穿織物的沖擊過程的有效性，對動態穿刺后的布面刺破效果進行仿真，對紗線的應力應變分布進行分析，并得到了沖擊系統的能量變化情況，主要結論如下：

1）刀具沖擊織物的過程可分為兩步：第一，刀具從紗線縫隙中刺入，紗線滑移拉伸，布面變形凸起，刀具速度下降至零;第二，紗線受到剪切或者拉伸作用斷裂，布面發生彈性恢復，推動刀具向相反方向移動。

2）織物的應力水平變化與應變同步。布面首先受力凸起，而后回彈，應力水平隨之先上升后下降。應力的分布集中在刀尖處、紗線交織點處與布面四周固定端處。當紗線斷裂時，斷裂紗線應力驟減，與之相交紗線上的交織點處的應力也因此驟減，應變減小，布面略有回彈。

3）刀具的能量少部分通過摩擦耗散，大部分被布面吸收，并轉化為紗線的內能。紗線的內能主要由紗線的彈性應變產生，少部分是蠕變和塑性應變能，且斷裂點的應力遠小于紗線的最大拉伸應力，因此紗線斷裂主要由刀具剪切作用導致，提高平紋織物的抗剪切性能是提高其防刺性能的關鍵。

參考文獻：

[1]WANG Q S， SUN R J， TIAN X， et al. Quasi-static puncture resistance behaviors of high-strength polyester fabric for soft body armor [J]. Results in Physics， 2016， 8（18）： 554-560.

[2]裴鵬英， 胡雨， 胡慧娜， 等. 柔性防彈防刺服開發關鍵技術[J]. 紡織導報， 2017（S1）： 62-65.

PEI Pengying， HU Yu， HU Huina， et al. Key technologies for developing flexible bullet-proof/stabresistant body armor [J]. China Textile Leader， 2017（S1）： 62-65.

[3]馬丕波， 蔣高明， 高哲， 等. 紡織結構復合材料沖擊拉伸研究進展[J]. 力學進展， 2013， 43（3）： 329-357.

MA Pibo， JIANG Gaoming， GAO Zhe， et al. Advances in impact tensile properties of 3-D textile structural composites [J]. Advances in Mechanics， 2013， 43（3）： 329-357.

[4]王艷飛， 孫耀寧， 孫文磊， 等. 纖維增強復合材料損傷行為及強度預測細觀力學建模研究進展[J]. 玻璃鋼/復合材料， 2014（6）： 83-89.

WANG Yanfei， SUN Yaoning， SUN Wenlei， et al. Advances of study with micromechanical modeling on damage behavior and strength predication of predication fiber reinforced composites [J]. Fiber Reinforced Plastics/Composites， 2014（6）： 83-89.

[5]施建偉. 基于ABAQUS復合材料層合板漸進損傷有限元分析[D]. 太原： 中北大學， 2015.

SHI Jianwei. Finite Element Analysis of Progressive Damage of Abaqus Composite Laminates [D]. Taiyuan： North University of China， 2015.

[6]周熠， 陳曉鋼， 張尚勇， 等. 超高分子質量聚乙烯平紋織物在柔性防彈服中的應用[J]. 紡織學報， 2016， 37（4）： 60-64.

ZHOU Yi， CHEN Xiaogang， ZHANG Shangyong， et al. Application of ultra-high molecular-weight polyethylene plain weave in soft body armour [J]. Journal of Textile Research， 2016， 37（4）： 60-64.

[7]邢京京， 錢曉明. 織物的防刺機制及刀具形狀對防刺性能的影響[J]. 紡織學報， 2017， 38（8）： 55-61.

XING Jingjing， QIAN Xiaoming. Stab-resistant mechanism of fabrics and influence of cutter shape on stab resistance [J]. Journal of Textile Research， 2017， 38（8）： 55-61.

[8]莊茁. 基于ABAQUS的有限元分析與應用[M]. 北京： 清華大學出版社， 2012.

ZHUANG Zhuo. Finite Element Analysis and Application Based on ABAQUS [M]. Beijing： Tsinghua University Press， 2012.

[9]張天陽. 機織物防刺性能的有限元分析[D]. 上海： 東華大學， 2012.

ZHANG Tianyang. Finite Element Analysis of Thorn Resistance of Woven Fabrics [D]. Shanghai： Donghua University， 2012.

[10]徐玲玲. 多層芳綸織物增強聚氨酯防刺性能的研究 [D]. 天津： 天津工業大學， 2017.

XU Lingling. Study on the Anti-Stab Performance of Multi-Layer Aramid Fabric Reinforced Polyurethane [D]. Tianjin： Tianjin Polytechnic University， 2017.