關注數學思想 培養數學素養—以低年級數學教學為例

任季芳

（福建省福州市馬尾區教師進修學校，福建福州 350015）

引 言

我國學生數學學習培養，歷經了由六大核心素養（數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析），到《全日制義務教育數學課程標準（2011年版）》明確提出的10個核心素養（數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力、模型思想、應用意識和創新意識）。這些核心素養是數學思想、數學方法或者關于數學的整體理解與把握，是學生數學素養的表現，其中最基本的核心素養有三個，即數學抽象、邏輯推理、數學建模。下面以低年級數學《1000以內數的認識》《排隊中的學問》教學為例，談談三個最基本的核心素養的培養。

一、數學抽象，讓學生的思維“動”起來

數學是一門抽象性、邏輯性很強的學科，數學知識的探究過程實質上也是數學抽象思想的感悟過程。教學中，教師要將抽象思想融入學生具體的數學學習過程中，讓學生在解決數學問題的過程中，逐步領悟抽象思想在數學中的運用[1]。

例如，教學二年級數學《1000以內數的認識》這一課時，為了讓學生感知1000的數量，讓學生4人一組，準確數出100粒紅豆裝入小袋子（見圖1），再讓10個小組代表將各組小袋子裝的100粒紅豆陸續倒入透明杯中，并進行實時投屏。學生們一邊看著一邊認真地數著：1個百、2個百、3個百……9個百（見圖2），此時教師強調：再添上1個百是幾個百？學生回答：10個百，教師接著問：10個一百是多少呢？師生共同得出：10個一百是一千，從而讓學生們感知1000粒紅豆的數量。

圖1 數紅豆

圖2 學生將紅豆倒入透明杯中

又如，教學一年級數學《排隊中的學問》一課時，讓學生們求：小麗和小宇之間有多少人（見圖3）？

圖3 小麗和小宇之間有多少人

有的學生喜歡用“數一數”的方法，而有的學生則喜歡用“畫一畫”的方法，教師給予學生們充分的時間交流合作，學生們將抽象的數量關系用不同的符號來表示，如□、△、○、☆等（見圖4）。

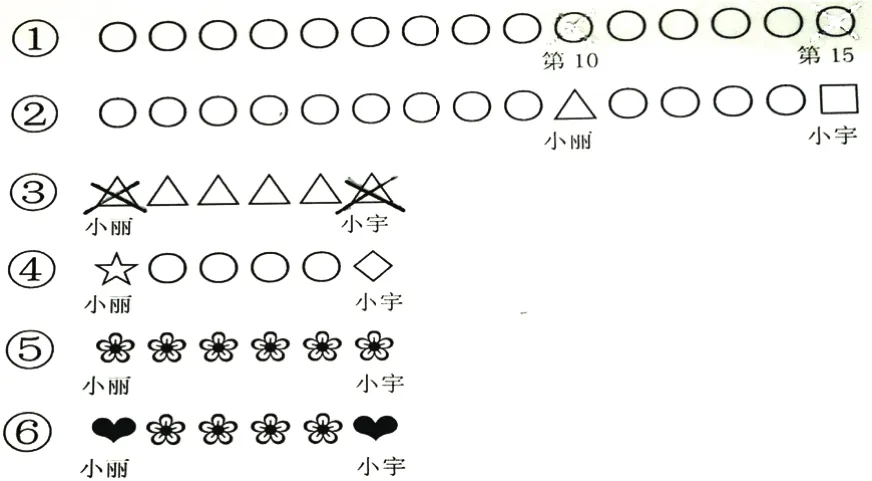
圖4 用不同符號表示抽象的數量關系

把抽象的數量關系轉化為學生容易理解的圖形，這一過程滲透著符號化思想，既降低了解題難度，又體現了多樣化的教學策略。符號化過程其實也是抽象過程，抽象思想與符號化思想如影隨形。抽象思想存在于數學學習的全過程，雖然低年級的數學知識看起來簡單，但實際上也充滿了抽象，教師要從低年級教學開始就關注抽象思想的滲透，培養學生數學素養。

二、邏輯推理，讓學生的思維“活”起來

推理是從一個或幾個已有的判斷得出另一個新判斷的思維形式。《義務教育數學課程標準(2011年版)》明確指出“推理能力的發展應貫穿在整個數學學習過程中。推理是數學的基本思維方式，也是人們在學習和生活中經常使用的思維方式……”。在利用數學解決各種實際問題的過程中，雖然大量的計算可以通過計算機來完成，但是就培養人的思維能力而言，推理能力仍然是至關重要的，因而推理能力必然是小學生數學素養的重要內容之一，教師要從低年級起就開始注重培養學生的這種能力。

例如，《1000以內數的認識》一課中有這樣的練習題練習找規律數數：

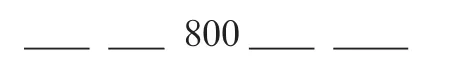
學生通過觀察發現，不僅可以100個100個地數、10個10個地數、1個1個地數，還可以從大到小數、從小到大數，因而得出六種結果：

發現規律的過程，也是推理的過程。在這過程中，學生又驚訝地發現此題還可以2個2個、5個5個、30個30個……地數，可以有無數種有規律的數法。在這一過程中教師盡量讓學生用語言說出自己的發現，從而使其數學思維得以豐富、提升。教師有意識地引領學生感悟推理的過程，經過長時間累積，邏輯推理就會慢慢內化成學生自己的數學素養。

在教學中滲透數學基本思想要經歷一個循環往復、螺旋上升的過程，而且常常是好幾種思想交織在一起，因此教師要從低年級開始，把抽象的數學思想逐漸揉進具體的數學知識內容中。

三、數學建模，讓學生的思維“亮”起來

數學模型是用數學語言概括地或近似地描述現實世界事物的特征、數量關系和空間形式的一種數學結構。數學的概念、定理、規律、法則、公式、性質、數量關系式等都是數學模型[2]。在小數教材中，模型無處不在，學生學習數學知識的過程，實際上就是對一系列數學模型的理解、把握的過程。

例如，教學《1000以內數的認識》拐彎數數時，借助算盤：（1）1個1個地數，從335數到342，數到339時，個位上9，添上1個珠子即10個1，個位上退去10個珠子，向十位進1個珠子，即340；（2）10個10個地數，從460數到530，數到490時，十位上9，添上1個珠子即10個10，十位上退去10個珠子，向百位進1個珠子，即500；（3）100個100個地數，從700數到1000，數到900時，百位上9，添上1個珠子即10個100，百位上退去10個珠子，向千位進1個珠子，即1000。在拐彎數數過程中建立模型：無論哪位滿十，都向前一位進1。利用建立的數學模型，讓學生撥珠練習“999添上1”，即個位9添上1滿10向十位進1，十位9添上1滿10向百位1，百位9添上1滿10向千位1，得出999后一個數是1000。數數中學生能熟練掌握并運用滿10進1的十進制原理，反映著模型思想在數學中的應用。

又如，教學《排隊中的學問》中的練習題，求“小麗和小宇之間有多少人？”（見圖5）

圖5 以畫圈的形式表示小麗和小宇之間有多少人

有的學生發現“求小麗和小宇之間有多少人？”還可用“算一算”的方法：“15-10-1＝4（人）”。在學生說明每一步算式所表示的意義后，教師配合學生將靜態畫面動態化，幫助學生理解算式的含義，如“15”表示到小宇為止有15人（課件閃動圖形總數15）；“-10”表示先減去到小麗為止的10人（課件閃動圖形表示10人部分）；“再-1”表示減去小宇這1個人（課件閃動圖形表示小宇1人部分），就得出小麗和小宇之間有4人。再通過“有20個同學排隊買票，小西排第10，小林排第18，它們之間有幾人？”的練習，讓學生發現“求兩數之間有多少”可以用“大數-小數-1”的計算方法得出。利用數學模型，“求兩數之間有多少”尤其兩數較大或中間的數較多時，“算一算”的方法更簡便。

模型思想是問題解決的重要形式，是培養學生“用”數學的重要途徑，有利于培養學生的創造能力。教師要從低年級教學開始就注重滲透模型思想，培養學生的數學素養。

結 語

數學思想方法正如杜甫的詩句：“好雨知時節，當春乃發生。隨風潛入夜，潤物細無聲”。希望數學思想就像春雨一樣不斷滋潤學生的心田，教師要從低年級開始，讓數學思想方法在學生心中“生根發芽”，并為后續的學習打下基礎，從而實現數學素養的提高。